Перпендикулярные прямые
Что такое перпендикулярные прямые, как их строить разными способами и где они встречаются в жизни — разберемся просто и наглядно

Принцип перпендикулярности помогает строить дома, рисовать карты, прокладывать дороги и даже создавать шрифты.
В древности мастера не знали про транспортир, но умели добиваться точности: отвес показывал, где вертикаль, а натянутый шнур — горизонталь. Так появлялись ровные стены и прочные перекрытия.
Сегодня мы используем линейки, треугольники и циркули, но принцип остался тем же — перпендикулярные линии делают все вокруг нас аккуратным и устойчивым. Разберемся, что такое перпендикулярные прямые, как их строить и какие задачи с ними решают.
Что такое перпендикулярные прямые
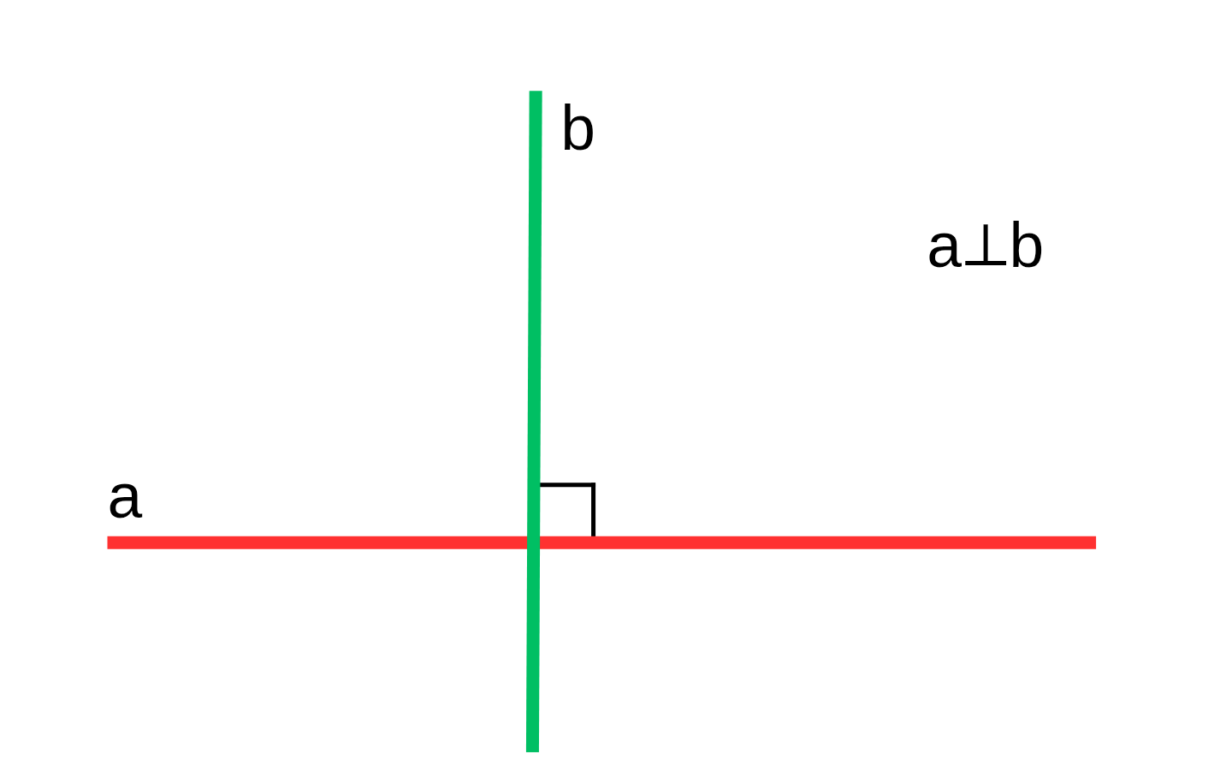
Перпендикулярные прямые — это две прямые, которые пересекаются под прямым углом, всегда равным 90°. Их обозначают знаком ⟂. Если прямая a перпендикулярна прямой b, это записывают как a ⟂ b, что означает «прямая a перпендикулярна прямой b». Такой способ записи используют математики по всему миру.
Перпендикулярные прямые встречаются не только в геометрии, но и в жизни. Ствол дерева растет вертикально, образуя прямой угол с землей. Когда дверь стоит ровно, она образует прямой угол с полом. Некоторые кристаллы имеют структуру с правильными прямыми углами. В 3:00 и 9:00 стрелки часов образуют угол в 90°. И даже в букве Т есть прямой угол.
В природе редко встречаются идеальные прямые углы — чаще их создает человек.
Полезная информация о перпендикулярных прямых
В таблице ниже собраны интересные факты, которые помогут лучше понять тему.
| Параметр перпендикулярных прямых | Пояснение |
|---|---|
| Сколько углов образуется | При пересечении двух перпендикуляров получается 4 одинаковых угла по 90° |
| Проверка угла | Угол чертежного треугольника или угол листа в клетку совпадает с прямым углом |
| В координатной геометрии | Оси X и Y на графике — классический пример перпендикулярных прямых |
| Измерения | Перпендикуляр от точки к линии — кратчайшее расстояние между ними |
| В треугольнике | Высота — это перпендикуляр, проведенный из вершины на противоположную сторону. |
Как построить перпендикулярные прямые
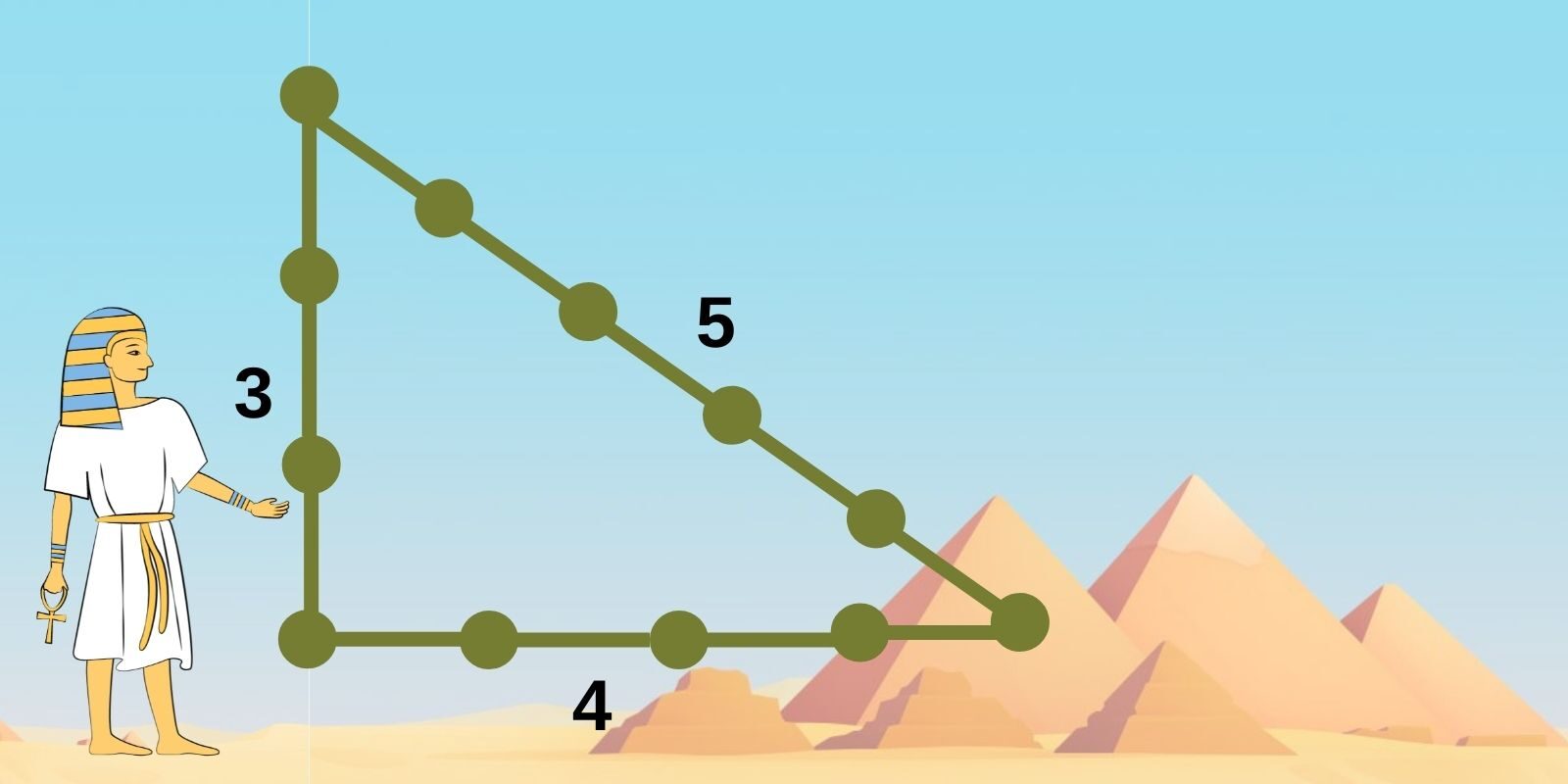
Еще в Древнем Египте строители использовали необычный способ для построения прямых углов. Они брали веревку и завязывали на ней 12 узлов на равном расстоянии. Затем веревку делили на части в соотношении 3:4:5 и связывали концы. Натягивая такую веревку между колышками, они получали прямоугольный треугольник с углом 90°.
Сегодня для построения перпендикуляров используют различные методы. Рассмотрим самые простые из них.
С помощью транспортира
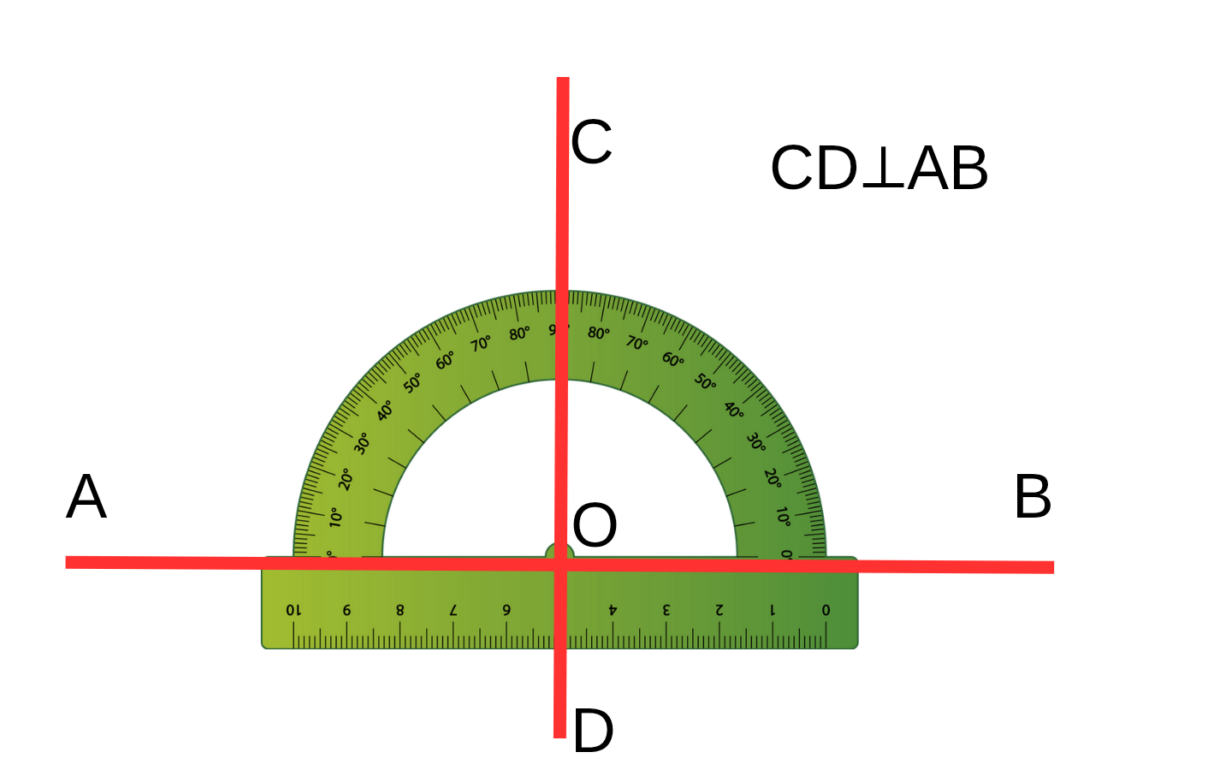
Предположим, у нас есть прямая AB. На ней отмечена точка O, через которую нужно провести перпендикуляр.
- Поставьте центр транспортира в точку O.
- Совместите нулевую отметку шкалы транспортира с прямой AB.
- Найдите на шкале отметку 90° и отметьте ее — это точка C.
- Уберите транспортир и проведите прямую через точки O и C.
- Продлите эту линию в обе стороны — получится прямая CD, перпендикулярная AB.
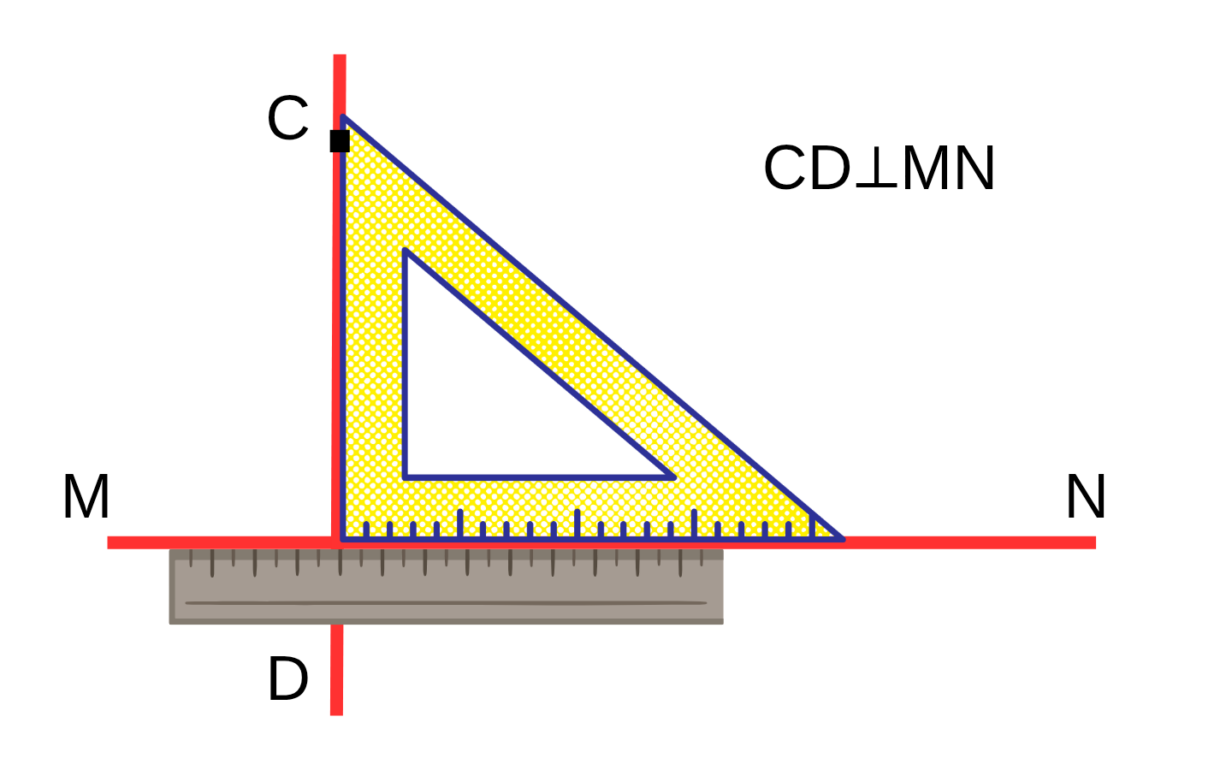
С помощью чертежного треугольника
У нас есть прямая MN, и на ней лежит точка P. Нужно провести через точку перпендикуляр к этой прямой.
- Приложите одну сторону прямого угла треугольника к MN.
- Совместите вершину прямого угла с точкой P.
- Проведите линию по второй стороне угла — это перпендикуляр.
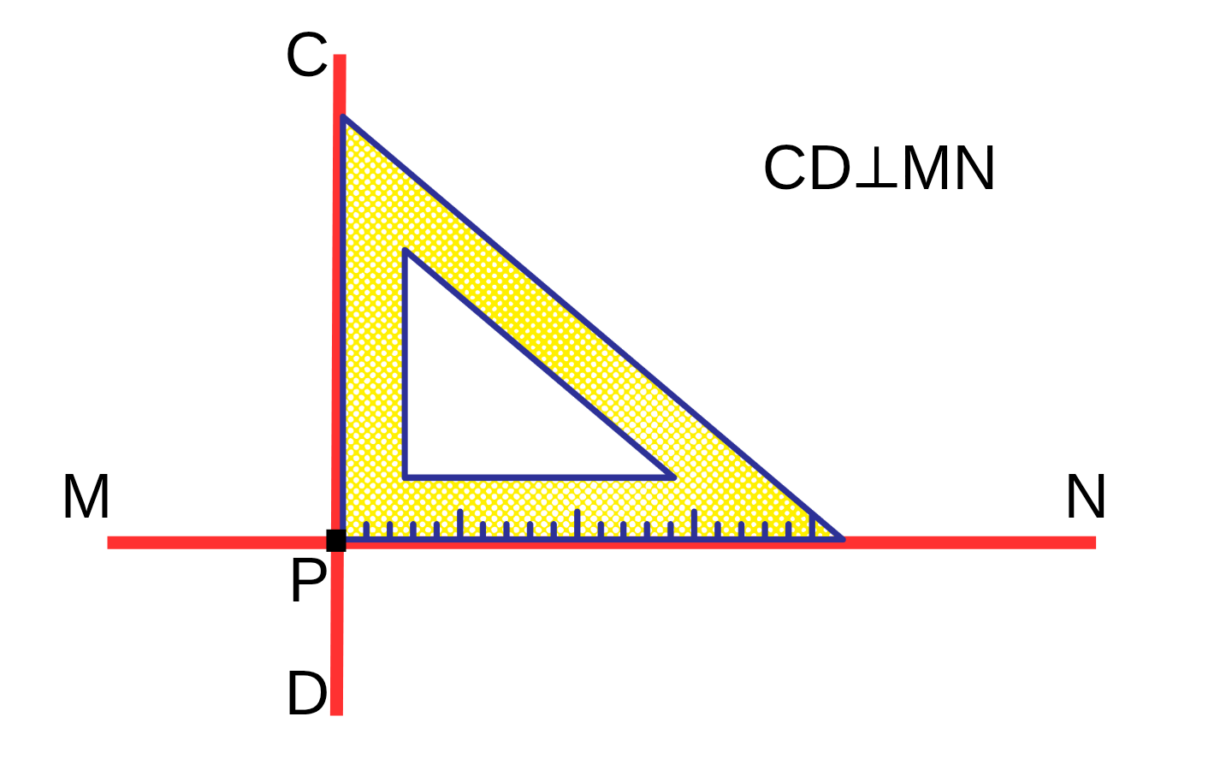
Если точка С находится вне прямой MN:
- Приложите одну сторону треугольника к MN.
- Поставьте линейку вдоль другой стороны треугольника.
- Сдвигайте треугольник по линейке, пока вершина угла не окажется в точке P.
- Проведите линию по второй стороне угла.
- Получится прямая CD, перпендикулярная MN.
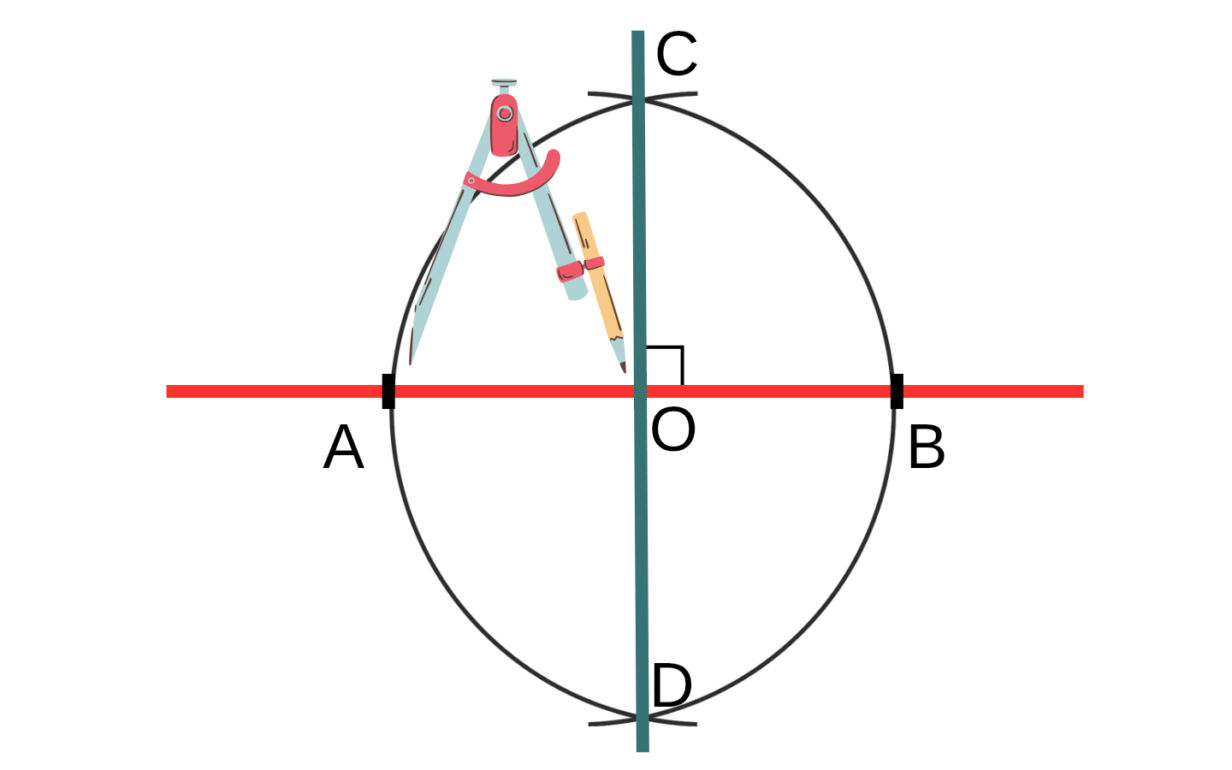
С помощью циркуля и линейки
Циркуль и линейка помогают построить перпендикуляр без измерения углов. Циркуль нужен для откладывания равных расстояний и построения дуг, линейка — для соединения точек прямыми линиями.
- Отметим точку на прямой О.
- Циркулем отложим от точки О равные отрезки. Обозначим их концы как A и B.
- Проведем окружности с центром в точках A и B и радиусом AB.
- Соединим точки пересечения окружностей линейкой. Обозначим их как C и D.
- Отрезок CD будет перпендикулярен AB.
Теорема о перпендикулярных прямых
Если у нас есть прямая линия и точка, которая не лежит на ней, то через эту точку можно провести только одну линию, пересекающую данную под прямым углом, то есть под 90°. Это значит, что:
- перпендикуляр из точки к прямой всегда можно построить;
- другого перпендикуляра из этой же точки к той же прямой не получится — он единственный.
Проще говоря, если выбрать точку вне линии, есть только один способ провести через нее прямую так, чтобы угол между ними был прямым.

Свойства перпендикулярных прямых
Перпендикулярные прямые подчиняются четким геометрическим законам, которые помогают решать задачи и строить точные чертежи. Рассмотрим их поподробнее.
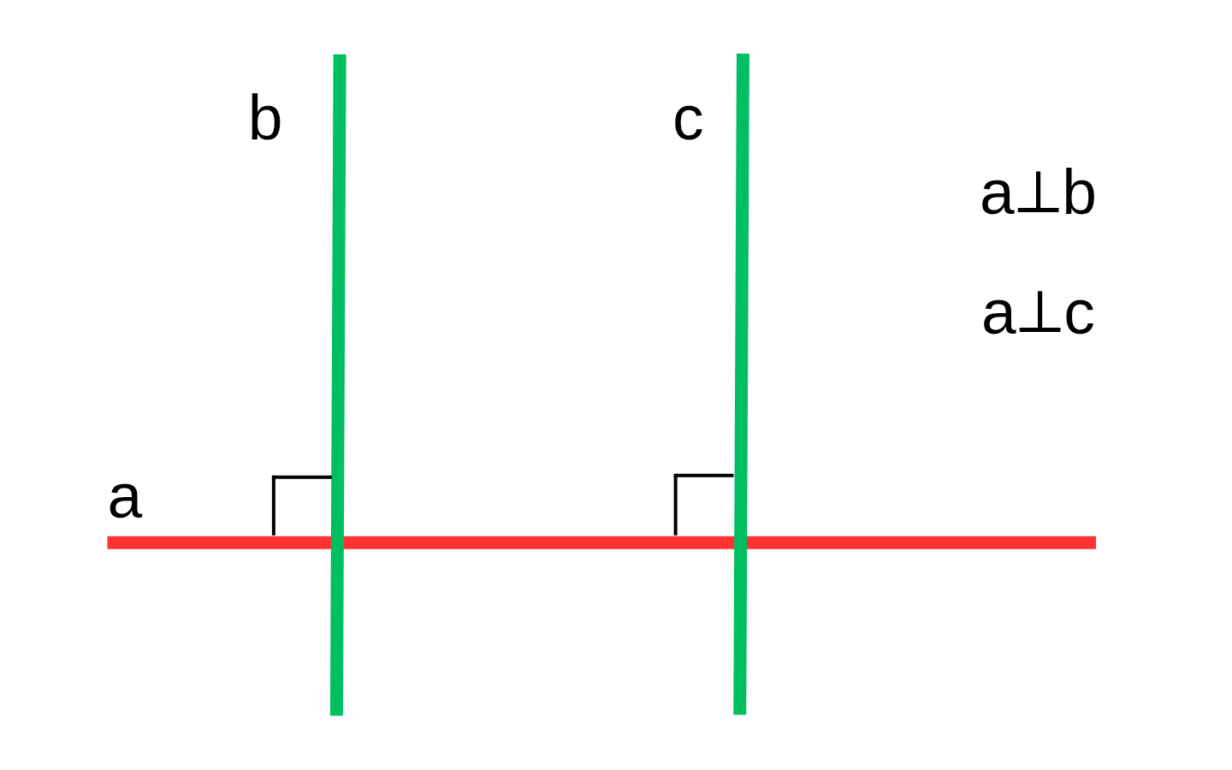
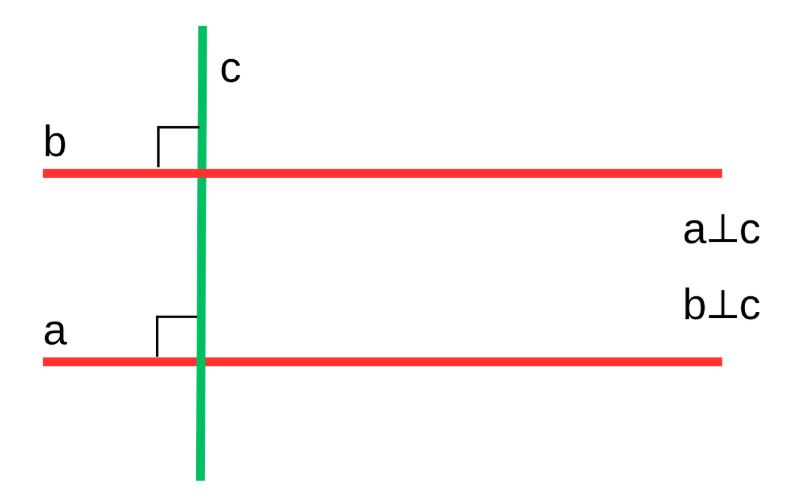
Если две прямые на плоскости перпендикулярны одной и той же третьей прямой, то они параллельны между собой.
Если прямая a⟂c и прямая b⟂c, то a||b.
Это значит, что если каждая из двух прямых образует угол 90°с одной и той же прямой, то они идут в одном направлении и никогда не пересекутся.
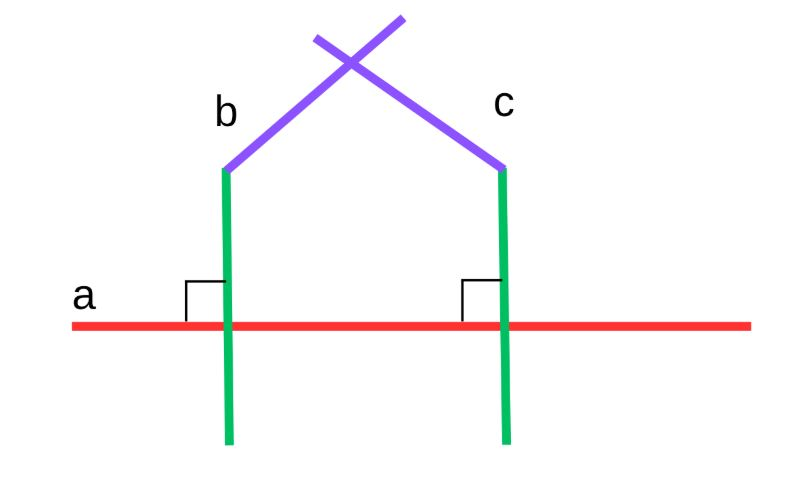
Так быть не может:
Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и второй.
Если a||b и прямая c⟂a, то c⟂b.
Иными словами, если одна прямая образует угол 90° с первой из двух параллельных, то с другой она образует такой же угол.
Задачи по теме «Перпендикулярные прямые»
Давайте потренируемся решать задачи.
Задача 1
От дома до прямой дороги 80 м. У дома есть наклонная тропинка длиной 160 м, по которой можно выйти к дороге. Какой путь будет самым коротким и на сколько метров тропинка длиннее кратчайшего пути?
Задача 2
Нужно понять, перпендикулярны ли боковые стенки полки ее основанию. Есть только лист бумаги (с ровным прямым углом). Опишите проверку и объясните, почему она работает.
Задача 3
Прямые AB и CD пересекаются в точке O и перпендикулярны (AB⟂CD). Внутри угла ∠AOC проведен луч OE так, что ∠AOE = 35°. Перечислите все прямые углы в точке O и найдите величины углов ∠EOC, ∠BOD, ∠AOB и ∠EOD.
Ответы к задачам
Проверим, что у вас получилось.
Задача 1
Кратчайшее расстояние от точки до прямой измеряется по перпендикуляру. Значит, самый короткий путь — идти от дома к дороге по линии, перпендикулярной дороге, и его длина равна 80 м.
Наклонная тропинка имеет длину 160 м. Разница между фактическим и кратчайшим путем равна 160 − 80 = 80 м.
Задача 2
У листа бумаги угол между соседними сторонами — 90°. Приложим угол листа впритык к углу «боковина–основание», совмещая одну сторону листа со стенкой, а другую — с основанием. Если границы листа ложатся без зазоров и разворотов вдоль обеих деталей одновременно, угол полки тоже прямой.
Если заметен зазор или одна сторона листа уходит в сторону, угол отличается от 90° — детали не перпендикулярны. Этот способ работает, потому что мы сравниваем проверяемый угол с эталонным прямым углом.
Задача 3
При пересечении перпендикулярных прямых получаются четыре прямых угла: ∠AOC = ∠COB = ∠BOD = ∠DOA = 90°.
Угол ∠AOE равен 35°, значит, оставшаяся часть прямого угла ∠EOC равна 90° – 35° = 55°.
Вертикальные углы равны, поэтому угол, вертикальный к ∠AOE, то есть ∠BOD, тоже равен 35°.
Угол ∠AOB — развернутый (сумма двух соседних прямых углов), следовательно, 180°.
Чтобы найти ∠EOD, заметим: луч OE находится в полуплоскости с OC, а OD перпендикулярен OC и составляет с ним угол 90°. Значит, ∠EOD равен ∠EOC + 90° = 55° + 90° = 145°.
Ответ: прямые углы — ∠AOC, ∠COB, ∠BOD, ∠DOA, остальные — ∠EOC = 55°, ∠BOD = 35°, ∠AOB = 180°, ∠EOD = 145°.
Популярные вопросы и ответы
Отвечает Дмитрий Малык, учитель математики и информатики высшей квалификационной категории, репетитор по подготовке к ЕГЭ и ОГЭ:
Какие примеры перпендикулярных прямых встречаются в жизни?
Все ли перпендикуляры к одной прямой параллельны друг другу?
Почему тему «Перпендикулярные прямые» изучают в 5–7 классах?
В каких заданиях ОГЭ и ЕГЭ встречаются перпендикулярные прямые?
В координатной геометрии требуется составить уравнение прямой, перпендикулярной данной, или проверить перпендикулярность, используя угловые коэффициенты.
Иногда встречаются вопросы на знание теоретических свойств, например нужно определить, верно ли утверждение: «Если две прямые на плоскости перпендикулярны третьей, то они параллельны».
В ЕГЭ перпендикуляры применяются в планиметрии при работе с высотами, серединными перпендикулярами, а также при решении задач, связанных с прямоугольными треугольниками.
В координатной геометрии они используются для нахождения уравнений прямых и проверки взаимного расположения линий, а в стереометрии — для определения перпендикулярности прямой и плоскости, построения общих перпендикуляров и вычисления расстояний между скрещивающимися прямыми.
Подобные задания встречаются как в базовой, так и в профильной части экзамена и требуют умения сочетать свойства фигур с алгебраическими методами решения.








