Рациональные неравенства: что такое, метод интервалов для решения рациональных неравенств, примеры, системы рациональных неравенств, задачи с ответами для 8-11 классов и подготовке к ОГЭ и ЕГЭ по математике.

Q: Как для решения рациональных неравенств определить знаки выражения на промежутках в методе интервалов?

Метод интервалов — это способ «увидеть», как ведет себя функция на числовой прямой. Сначала мы находим точки, где выражение обнуляется или становится неопределенным, и отмечаем их на прямой. Эти точки делят всю числовую прямую на промежутки.Главная идея в том, что внутри каждого промежутка знак выражения не меняется. Достаточно взять одно любое число из промежутка и проверить, будет ли значение положительным или отрицательным. После этого этот знак сохраняется для всего интервала.Многие школьники сначала воспринимают метод интервалов как «таблицу со знаками», но важно понимать: за таблицей стоит простая логика — мы анализируем, как ведет себя функция между своими нулями и точками разрыва.И здесь есть особая ценность: метод интервалов — это универсальный ключ. Он работает не только для рациональных неравенств, но и для квадратных, дробно-рациональных, а в старших классах даже для тригонометрических. Освоив его один раз, ученик получает инструмент, который помогает решать целый ряд задач.

Q: Почему тему по алгебре «Рациональные неравенства» изучают в 8–11 классах?

Потому что именно в этот период у школьников уже есть нужная база: они умеют решать линейные и квадратные неравенства, знают свойства дробей и понимают, что такое область определения. Рациональные неравенства становятся следующим шагом, где эти знания нужно соединить.В 8–9 классе ребята начинают с простых примеров: знаменатель не равен нулю, числитель можно разложить на множители, дальше применяется метод интервалов. А в 10–11 классах тема становится более сложной: появляются задания с параметрами, более громоздкие выражения, где без системного подхода уже не обойтись.Такие задачи воспитывают у школьников особую внимательность: нужно отслеживать условия, проверять каждый промежуток, не упускать исключений. Это не просто вычисления, а умение мыслить аккуратно и логично.

Q: В каких заданиях ОГЭ и ЕГЭ по математике понадобится умение решать рациональные неравенства?

В ОГЭ рациональные неравенства встречаются во второй части. Например, в задачах, где нужно решить дробное выражение или учесть область определения, чтобы исключить «запрещенные» значения. Там метод интервалов помогает быстро и наглядно найти решение.В ЕГЭ профильного уровня рациональные неравенства чаще всего появляются в заданиях №9 и №15. Но на этом их роль не заканчивается. Они могут встретиться и в параметрических задачах №18, и в темах с логарифмами или тригонометрией. Везде, где есть дроби и условия на знак выражения, работает именно метод интервалов. Поэтому умение решать рациональные неравенства — это базовый инструмент для экзамена, который напрямую влияет на количество набранных баллов.Очень часто ошибки в рациональных неравенствах связаны не с методом интервалов, а с тем, что школьники забывают проверить знаменатель. Если точка делает знаменатель равным нулю, она обязательно исключается из ответа, даже если по методу интервалов она подходит. Поэтому правило простое: сначала ОДЗ, потом решение. Это поможет избежать обидных потерь баллов на экзамене.

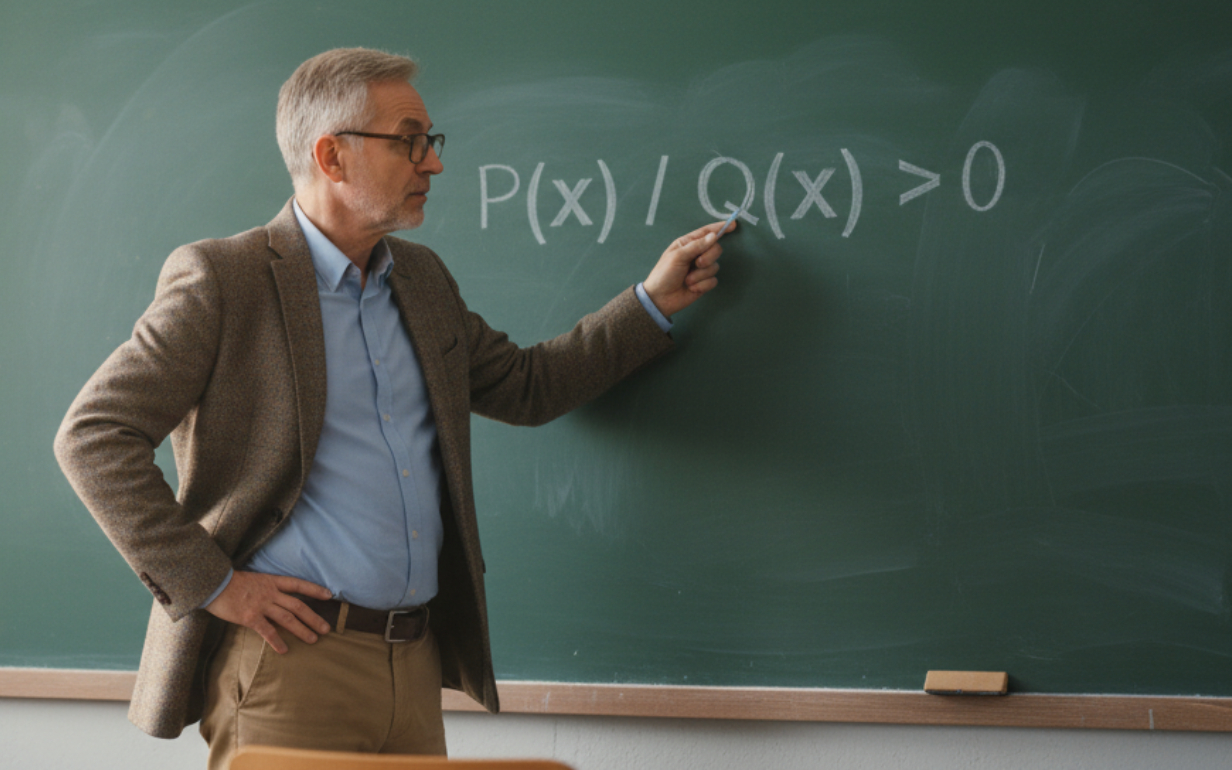
Вы уже умеете работать с линейными и квадратными неравенствами, теперь пришло время освоить новый уровень. Рациональные неравенства, где переменная скрывается в знаменателе, это не просто очередная тема из учебника. Они представляют собой ключевой инструмент для решения практических задач, помогают точно определять допустимые диапазоны значений в различных областях, например, при расчете концентрации веществ или определении экономической эффективности. В отличие от уравнений, здесь нельзя просто переносить выражения через знак неравенства. Вместо этого мы будем использовать метод интервалов, который позволяет наглядно представить решение на числовой прямой.

Что такое рациональные неравенства в алгебре

Рациональное неравенство — это любое неравенство, содержащее рациональные выражения, то есть выражения, которые можно представить в виде отношения двух многочленов.

С этой точки зрения, изученные ранее неравенства тоже являются рациональными:

линейное 3x — 6 > 0 можно записать как (3x-6)/1 > 0;
квадратное x² — 4 ≤ 0 можно записать как (x²-4)/1 ≤ 0.

Однако в школьной практике для красоты и удобства термин рациональные неравенства закрепился за неравенствами, в которых переменная находится в знаменателе, — дробно-рациональные неравенства. Это более сложный случай, требующий особого подхода и учета ограничений.

Общий вид дробно-рационального неравенства с одной переменной:

P(x) / Q(x) > 0,

где:

P(x) и Q(x) — многочлены,
Q(x) ≠ 0 (ключевое условие, так как на ноль делить нельзя).

Полезная информация о рациональных неравенствах

При работе с рациональными неравенствами важно учитывать их тип. От этого зависит выбор метода решения и учет ограничений. Следующая таблица поможет систематизировать основные виды рациональных неравенств и их особенности.

Тип рационального неравенства	Важные особенности
Строгое (> или <)Пример: (x — 2)/(x + 3) > 0	Точки, где дробь равна нулю (нули числителя) или не существует (нули знаменателя), не входят в ответ. Граничные точки на числовой прямой показываются выколотыми
Нестрогое (≥ или ≤)Пример: (x² — 4)/(x — 1) ≤ 0	Точки, где дробь равна нулю (нули числителя), входят в ответ. Точки, где дробь не существует (нули знаменателя), никогда не входят в ответ
Целое (знаменатель = 1)Пример: (5x — 4)(x + 2)(3 — x) > 0	Фактически является линейным, квадратным неравенством или неравенством высших степеней. Решается методами, изученными ранее, но также применим метод интервалов
Дробно-линейноеПример: (2x -1)/(x + 5) < 0	Частный случай, где и числитель, и знаменатель — линейные выражения
Высоких степенейПример: (x — 1)(x + 2)³/(x — 4)² ≥ 0	Требует внимательного анализа кратности корней. При четной кратности знак на интервалах не меняется, при нечетной — меняется

Что такое решение неравенства

Решить неравенство — значит найти все значения переменной x, при которых неравенство становится верным, с учетом всех ограничений.

В отличие от уравнений, решения рациональных неравенств чаще всего представляют собой не отдельные точки, а бесконечное множество значений — числовой промежуток или объединение нескольких промежутков.

Рассмотрим два примера:

уравнение (x — 2)/(x + 3) = 0 → x = 2
неравенство (x — 2)/(x + 3) > 0 → x ∈ (-∞; -3) ∪ (2; +∞)

Типы решений неравенств

Результат рационального неравенства может быть записан различными способами. Существует три основные формы записи решений.

1. Запись в виде неравенства. Является самым простым способом представить решение. Типы записи:

x > a, x < a — строгий ответ
x ≥ a, x ≤ a — нестрогий ответ
a < x < b, a ≤ x ≤ b, a < x ≤ b, a ≤ x < b — двойное неравенство

Примеры:

(x — 1)/(x + 2) > 0 → x < -2 или x > 1

(2x + 3)/(x — 4) ≤ 0 → -1,5 ≤ x < 4

2. Запись в виде числового промежутка. Является более формальной математической записью.

Типы промежутков:

(a; b) — интервал (a < x < b)
(a; b] — полуинтервал (a < x ≤ b)
[a; b) — полуинтервал (a ≤ x < b)
[a; b] — отрезок (a ≤ x ≤ b)
(-∞; a) — открытый луч (x < a)
(a; +∞) — открытый луч (x > a)
(-∞; a] — закрытый луч (x ≥ a)
[a; +∞) — закрытый луч (x ≥ a)

Примеры:

(x — 3)/(x + 1) < 0 → x ∈ (-1; 3)

(x² — 9)/(x — 2) ≥ 0 → x ∈ [-3; 2) ∪ [3; +∞)

3. Графическое представление. Наглядный способ изображения решения на числовой прямой.

Правила обозначений:

● — точка включается (для знаков ≥ или ≤)
○ — точка не включается (для знаков > или <)
→ или ← — направление решения

Примеры:

(x — 2)/(x + 1) > 0 → x ∈ (-∞; -1) ∪ (2; +∞)

(x — 3)/(x + 2) ≤ 0 → x ∈ (-2; 3]

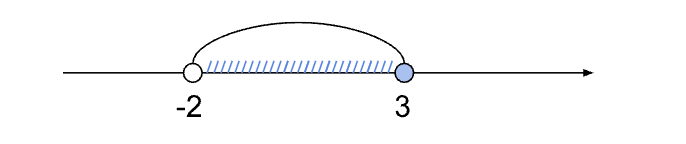
Все три формы записи решений являются равнозначными и используются в зависимости от конкретной задачи или требований. В школьной практике часто требуется представлять решение всеми тремя способами.

это интересно

Многочлены

Вспомним все методы разложения многочленов на множители

подробнее

Метод интервалов для решения рациональных неравенств

Метод интервалов — это единственный универсальный и самый наглядный метод решения рациональных неравенств, суть которого — определить знак дроби на каждом интервале между критическими точками. Он превращает сложные алгебраические выражения в наглядную схему на числовой прямой. Освоив этот алгоритм, вы сможете решать любые рациональные неравенства.

Алгоритм решения:

Перенести все слагаемые в одну сторону, чтобы справа остался 0.
Привести левую часть к виду одной дроби, если дробей несколько.
Разложить числитель и знаменатель на множители.
Найти критические точки: корни числителя — точки, где дробь равна нулю, и корни знаменателя — точки, где дробь не существует.
Отметить эти точки на числовой прямой. Точки из знаменателя всегда выколоты, точки из числителя — выколоты для строгих неравенств и закрашены для нестрогих.
Определить знак левой части неравенства на каждом интервале, подставляя любую точку из него. Важно не брать граничные точки интервалов. Также можно определить знак лишь на одном интервале, а на остальных расставить знаки, чередуя их, но используя правило: кратность корня (четная или нечетная степень множителя) влияет на смену знака при переходе через точку. При четной кратности знак не меняется, при нечетной — меняется.
Выбрать интервалы с нужным знаком согласно исходному неравенству: > 0 — «+», < 0 — «-». Не забыть проверить, включаются ли граничные точки.

Частые ошибки при решении рациональных неравенств:

не учтена область допустимых значений (ОДЗ) — включили точку, в которой знаменатель равен нулю;
неправильно расставлены знаки на интервалах, не учтена кратность корней;
перепутаны правила выбора интервалов для знаков > и <.

Примеры

Решим неравенство:

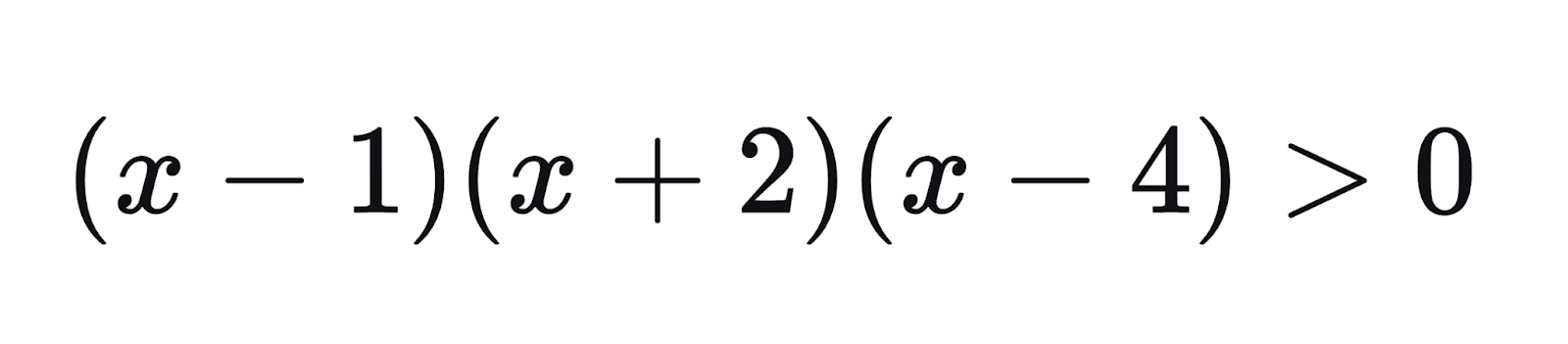
Критические точки: x = -2, x = 1, x = 4.

Отмечаем точки на числовой прямой. Они все выколоты, так как неравенство строгое.

Определяем знаки на интервалах. Рассмотрим интервал x < -2. Возьмем точку x = -3, подставляем в левую часть неравенства: (-)×(-)×(-) = (-). Далее знаки чередуются.

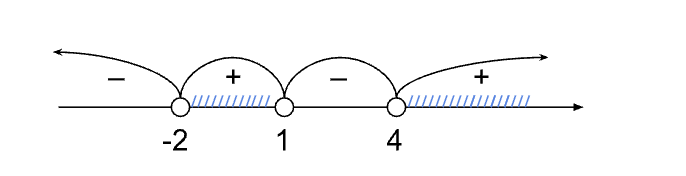
Выбираем интервалы со знаком «+», так как знак неравенства >:

x ∈ (-2; 1) ∪ (4; +∞).

Ответ: x ∈ (-2; 1) ∪ (4; +∞)

Решим неравенство:

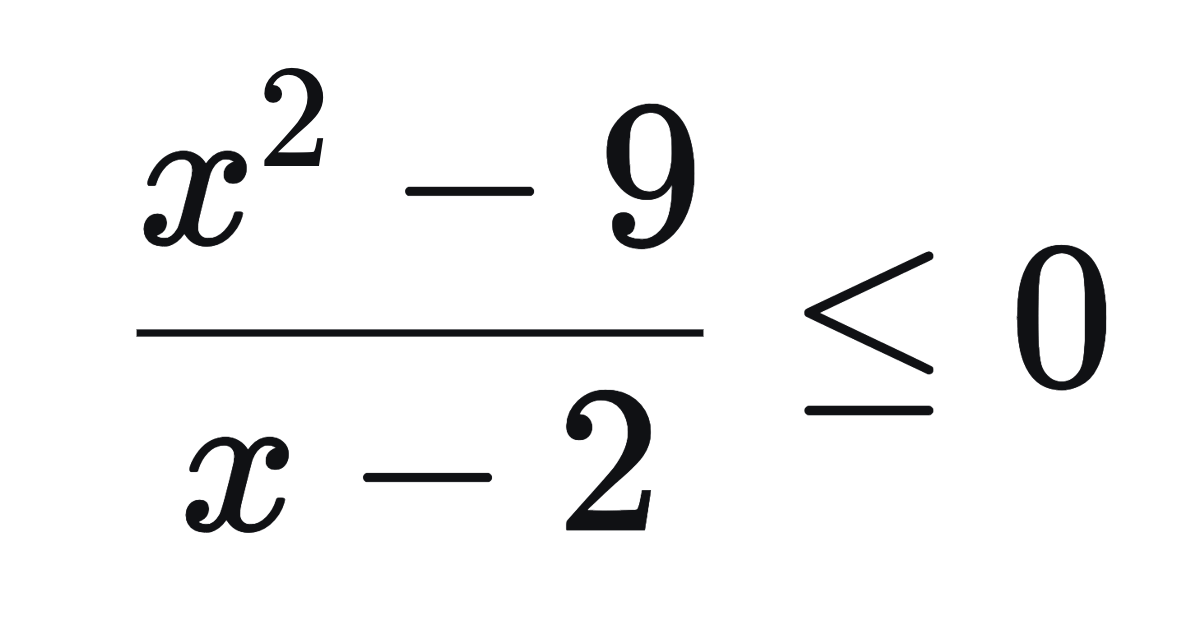
Разложим числитель на множители: ((x-3)(x+3))/(x-2) ≤ 0.

Критические точки: x = -3, x = 2, x = 3.

Отмечаем точки на числовой прямой. Точка x = 2 выколота, так как в ней дробь не существует, точки x = -3 и x = 3 включены, так как неравенство нестрогое.

Определяем знаки на интервалах. Рассмотрим интервал x < -3. Возьмем точку x = -4, подставляем в левую часть неравенства: (-)×(-)/(-) = (-). Далее знаки чередуются.

Выбираем интервалы со знаком «-», так как знак неравенства ≤:

x ∈ (-∞; -3] ∪ (2; 3].

Ответ: x ∈ (-∞; -3] ∪ (2; 3]

Решим неравенство:

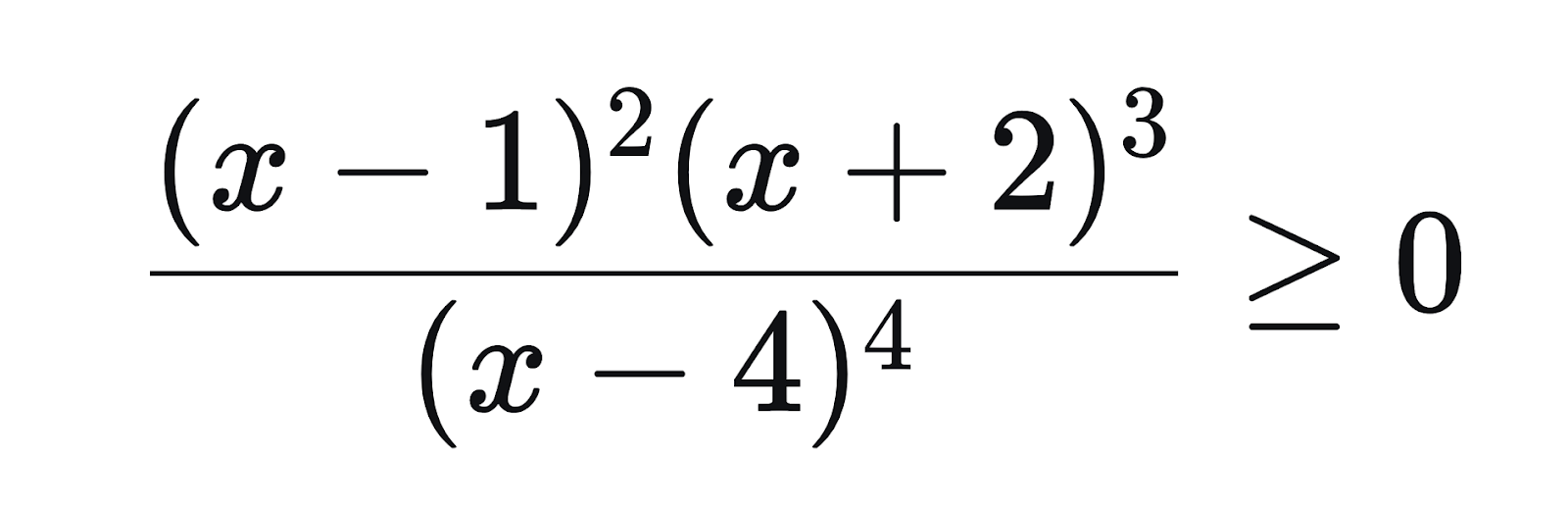
Критические точки: x = -2, x = 1, x = 4.

Отмечаем точки на числовой прямой. Точка x = 4 выколота, так как в ней дробь не существует, точки x = -2 и x = 1 включены, так как неравенство нестрогое.

Определяем знаки на интервалах. Рассмотрим интервал x < -2. Возьмем точку x = -3, подставляем в левую часть неравенства: (-)²×(-)³/(-)⁴ = (-). Далее для расстановки знаков учитываем кратность:

(x — 1)² — четная кратность, знаки не чередуются
(x + 2)³ — нечетная кратность, знаки чередуются
(x — 4)⁴ — четная кратность, знаки не чередуются

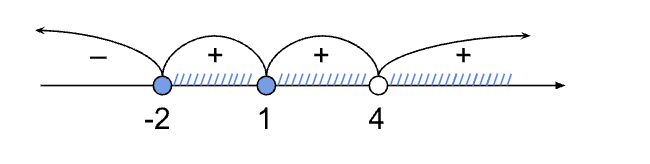
Выбираем интервалы со знаком «+», так как знак неравенства ≥:

x ∈ [-2; 4) ∪ (4; +∞).

Ответ: x ∈ [-2; 4) ∪ (4; +∞)

Системы рациональных неравенств

В систему могут входить самые разные типы неравенств — не только рациональные, но и линейные, квадратные, иррациональные, показательные и другие. Важно понимать: решением системы будет являться пересечение решений всех неравенств, входящих в нее. То есть мы ищем такие значения переменной, которые удовлетворяют каждому условию системы одновременно.

Алгоритм:

Решить каждое неравенство системы в отдельности.
Изобразить решение всех неравенств на одной числовой прямой.
Найти пересечение этих решений — область, которая удовлетворяет всем неравенствам одновременно.

Примеры

Решим систему неравенств:

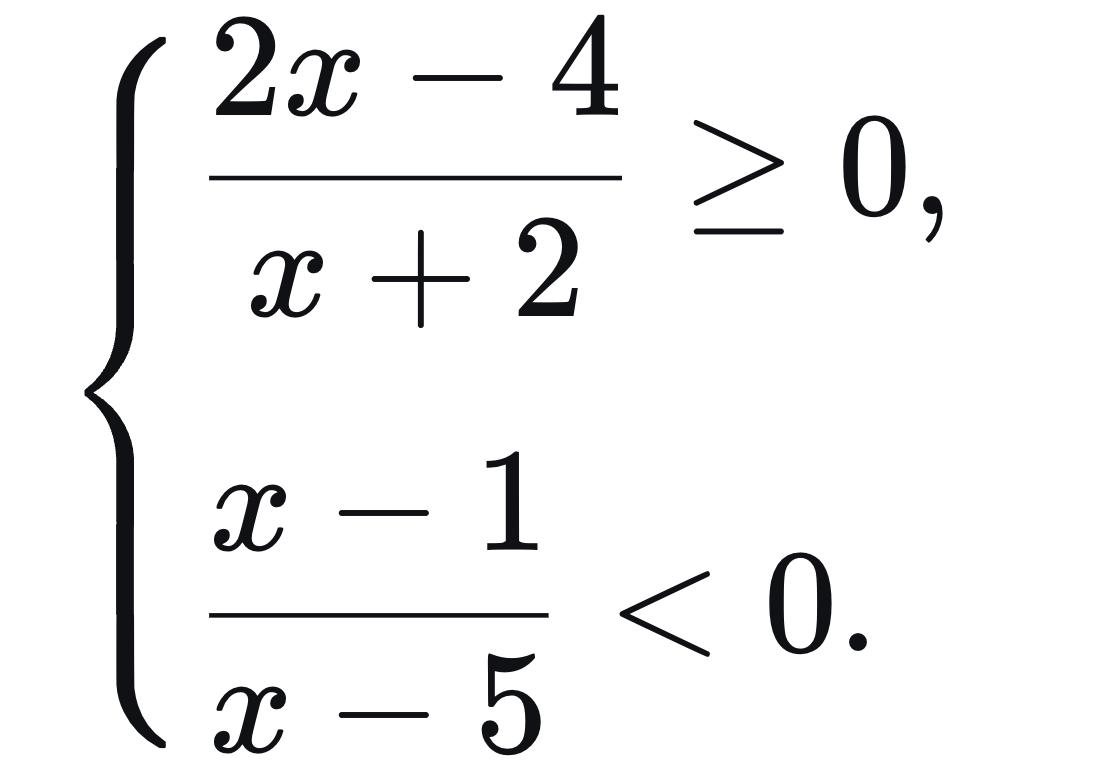
Решаем первое неравенство: (2x — 4)/(x + 2) ≥ 0 → x ∈ (−∞; −2) ∪ [2; +∞).

Решаем второе неравенство: (x — 1)/(x — 5) < 0 → x ∈ (1; 5).

Изображаем решения неравенств на числовой прямой:

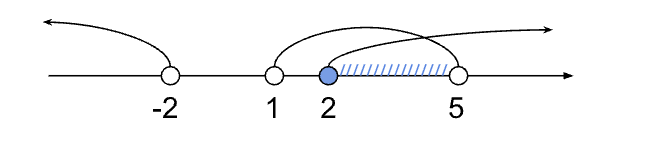
Находим пересечение x ∈ (−∞; −2) ∪ [2; +∞) и x ∈ (1; 5).

Общее решение: x ∈ [2; 5).

Ответ: x ∈ [2; 5)

Решим систему неравенств:

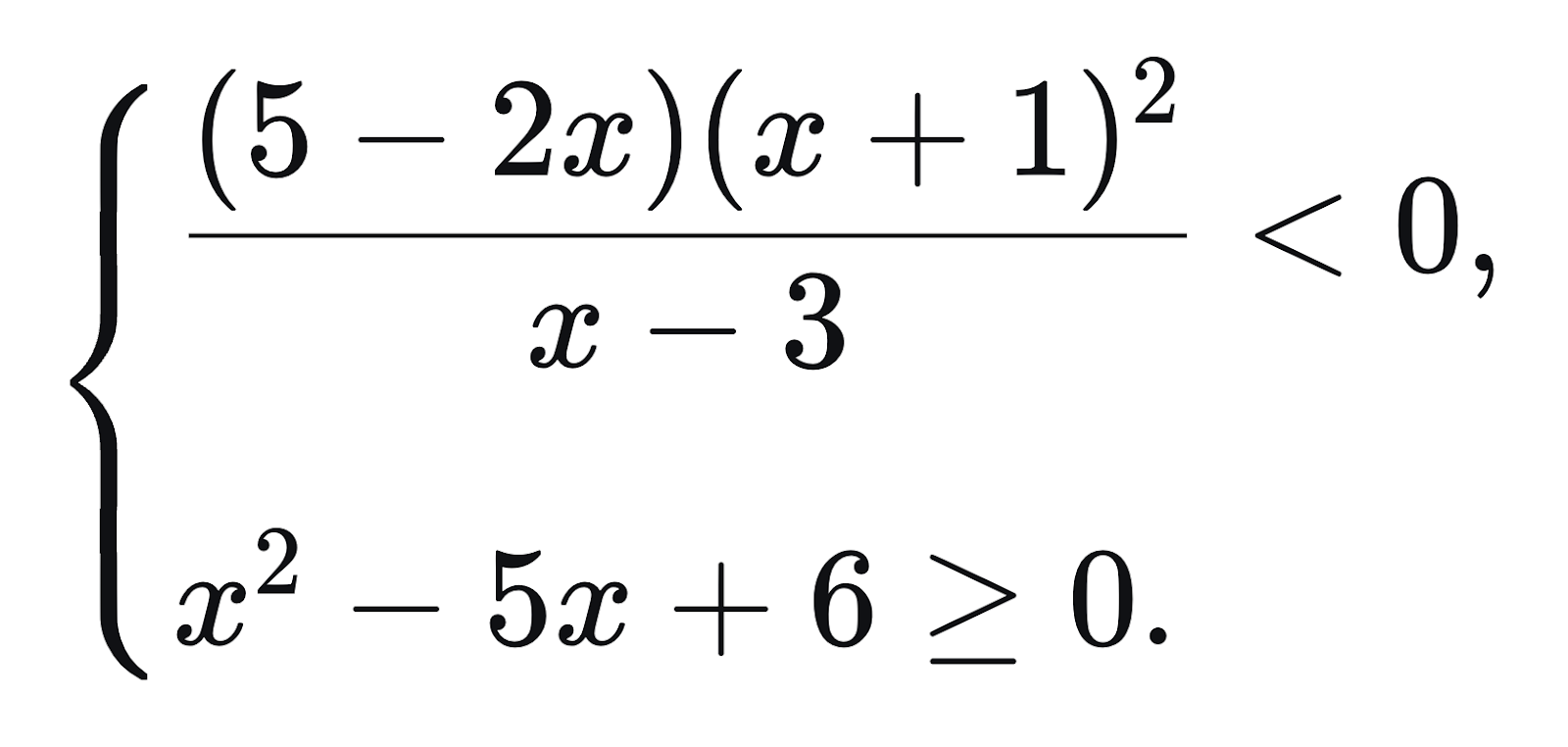
Решаем первое неравенство: (5 — 2x)(x + 1)²/(x — 3) < 0 → x ∈ (−∞; −1) ∪ (−1; 2,5) ∪ (3; +∞).

Решаем второе неравенство: x² — 5x + 6 ≥ 0 → x ∈ (−∞; 2] ∪ [3; +∞).

Изображаем решения неравенств на числовой прямой:

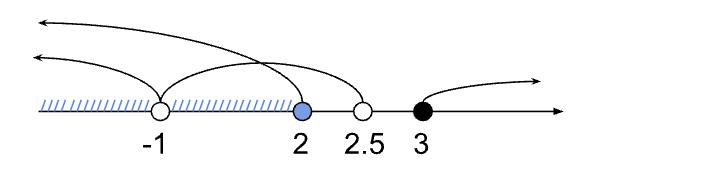
Находим пересечение x ∈ (−∞; −1) ∪ (−1; 2,5) ∪ (3; +∞) и x ∈ (−∞; 2] ∪ [3; +∞).

Общее решение: x ∈ (−∞; −1) ∪ (−1; 2] ∪ (3; +∞).

Ответ: x ∈ (−∞; −1) ∪ (−1; 2] ∪ (3; +∞)

Задачи по теме «Рациональные неравенства»

Попрактикуйтесь в решении рациональных неравенств разного типа. Для каждой задачи используйте метод интервалов и не забывайте про область определения.

Задача 1

Решите неравенство:

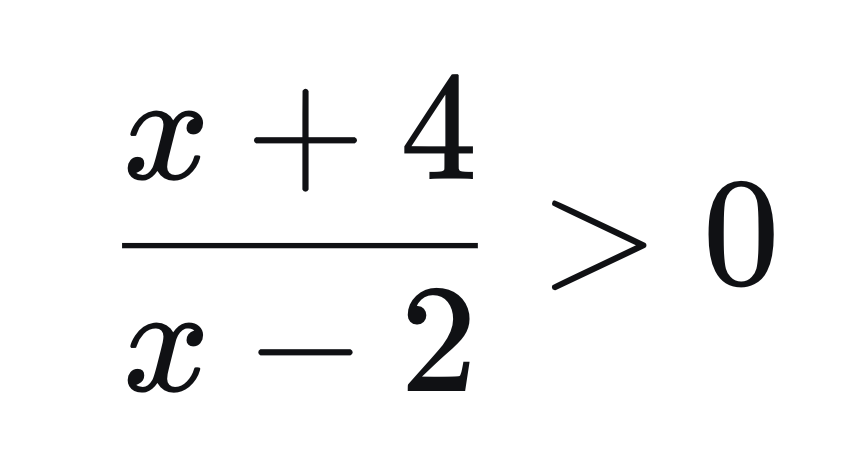
Задача 2

Решите неравенство:

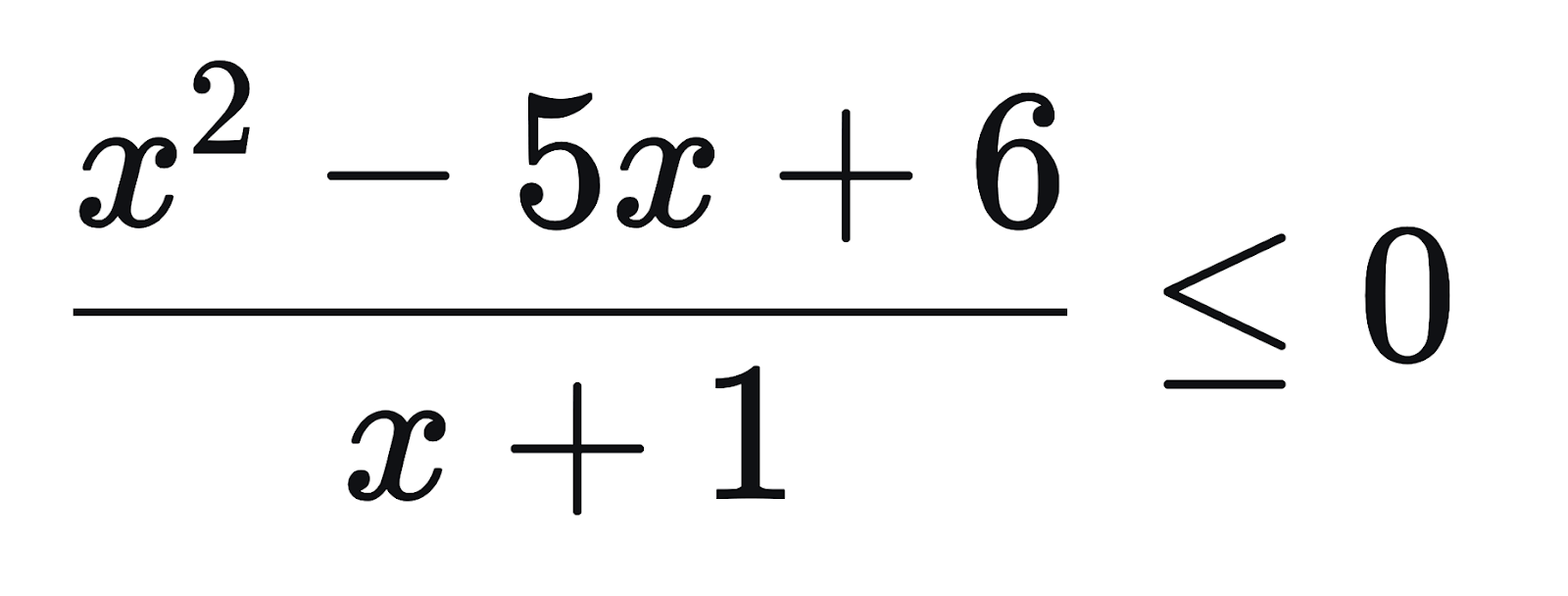
Задача 3

Решите систему неравенств:

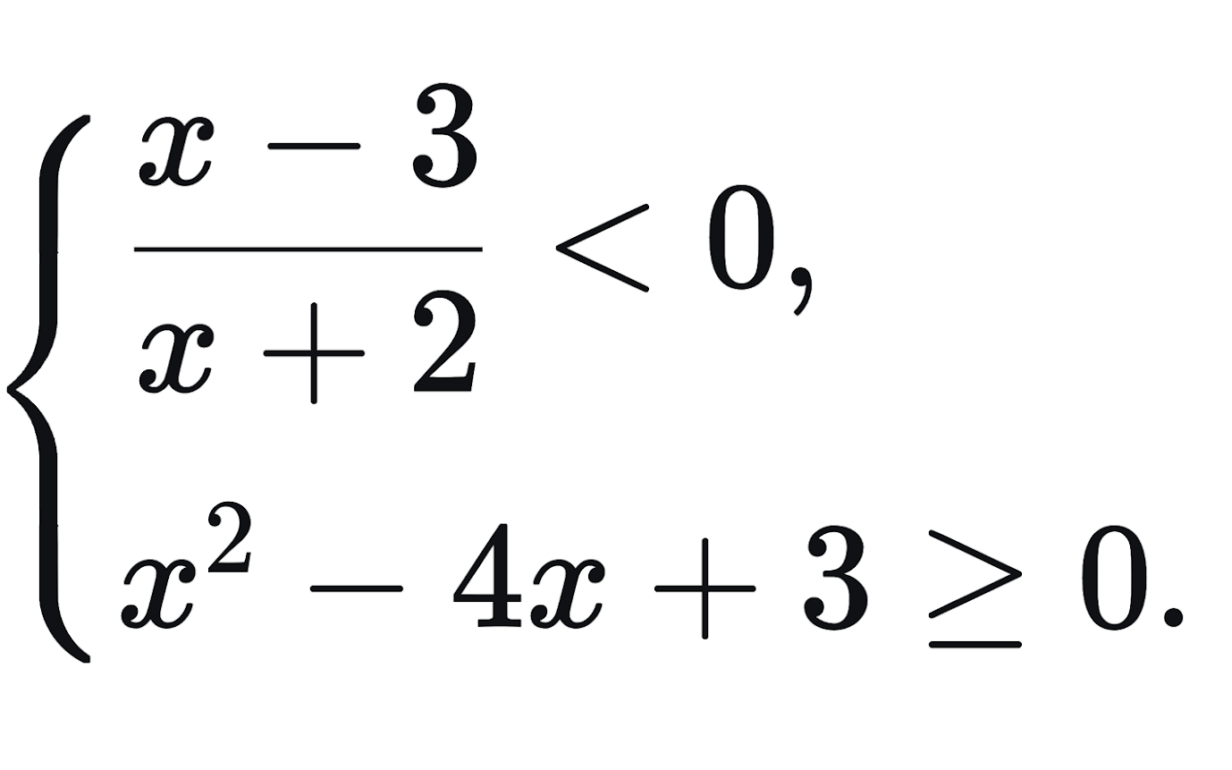
Ответы к задачам

Ниже приведены подробные решения всех задач. Если ваш ответ не совпал с приведенным — не расстраивайтесь. Внимательно изучите ход решения, найдите, на каком этапе была допущена ошибка, и постарайтесь понять ее причину.

Задача 1

Критические точки: x = -4, x = 2.

Отмечаем точки на числовой прямой. Они обе выколоты, так как неравенство строгое.

Определяем знаки на интервалах. Рассмотрим интервал x < -4. Возьмем точку x = -5, подставляем в левую часть неравенства: (-)/(-) = (+). Далее знаки чередуются.

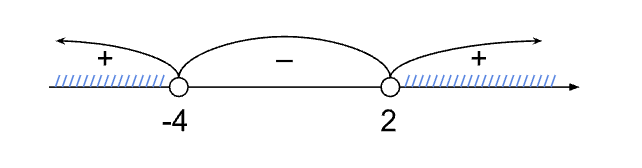
Выбираем интервалы со знаком «+», так как знак неравенства >:

x ∈ (-∞; -4) ∪ (2; +∞).

Ответ: x ∈ (-∞; -4) ∪ (2; +∞)

Задача 2

Разложим числитель на множители: ((x-2)(x-3))/(x+1) ≤ 0.

Критические точки: x = -1, x = 2, x = 3.

Отмечаем точки на числовой прямой. Точка x = -1 выколота, так как в ней дробь не существует, точки x = 2 и x = 3 включены, так как неравенство нестрогое.

Определяем знаки на интервалах. Рассмотрим интервал x < -1. Возьмем точку x = -2, подставляем в левую часть неравенства: (-)(-)/(-) = (-). Далее знаки чередуются.

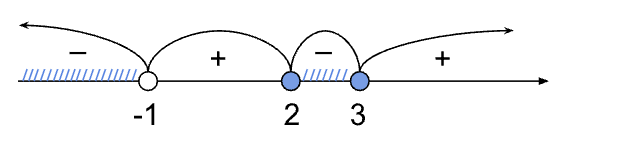
Выбираем интервалы со знаком «-», так как знак неравенства ≤:

x ∈ (-∞; -1) ∪ [2; 3].

Ответ: x ∈ (-∞; -1) ∪ [2; 3]

Задача 3

Решаем первое неравенство: (x — 3)/(x + 2) < 0 → x ∈ (-2; 3).

Решаем второе неравенство: x² — 4x + 3 ≥ 0 → x ∈ (-∞; 1] ∪ [3; +∞).

Изображаем решения неравенств на числовой прямой:

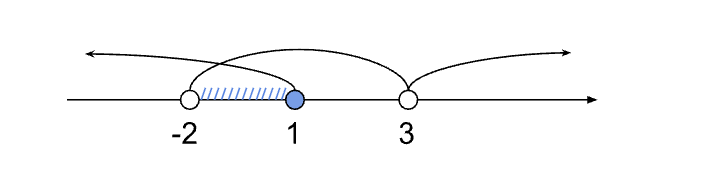
Находим пересечение x ∈ (-2; 3) и x ∈ (-∞; 1] ∪ [3; +∞).

Общее решение: x ∈ (-2; 1].

Ответ: x ∈ (-2; 1]

Рациональные неравенства

Что такое рациональные неравенства в алгебре

Полезная информация о рациональных неравенствах

Что такое решение неравенства

Типы решений неравенств

Метод интервалов для решения рациональных неравенств

Примеры

Системы рациональных неравенств

Примеры

Задачи по теме «Рациональные неравенства»

Ответы к задачам

Популярные вопросы и ответы

Как для решения рациональных неравенств определить знаки выражения на промежутках в методе интервалов?

Почему тему по алгебре «Рациональные неравенства» изучают в 8–11 классах?

В каких заданиях ОГЭ и ЕГЭ по математике понадобится умение решать рациональные неравенства?

Читайте также