Римские цифры
Разберемся, что такое римские цифры, как устроена эта система и по каким правилам записываются числа. Научимся легко переводить записи в привычные арабские числа и обратно
Мы так привыкли к арабским цифрам, что другие системы кажутся чем-то сложным и архаичным. Но стоит лишь разобраться в логике римской нумерации, как становится понятна ее элегантность и простота. Римские цифры окружают нас повсюду: в нумерации веков, на циферблатах часов, в титрах фильмов и именах монархов.
В отличие от позиционной системы арабских цифр, где значение цифры зависит от ее положения, римская система использует принцип сложения и вычитания значений основных знаков. Это делает ее менее удобной для вычислений, но невероятно интересной для изучения. Давайте вместе освоим этот древний и красивый числовой язык.
Что такое римские цифры в математике
Римские цифры — это буквы латинского алфавита, которые используются для записи чисел по определенным правилам. Эта система зародилась в Древнем Риме и активно использовалась по всей Европе до позднего Средневековья, когда ее начала вытеснять более удобная арабская система. Главное отличие от арабских цифр — отсутствие нуля и непозиционный принцип: величина числа не зависит от порядка цифр, а определяется по правилам сложения и вычитания их значений.
Полезная информация о римских цифрах
Основу системы римских цифр составляют всего семь ключевых символов-букв латинского алфавита. Главная красота и гениальность системы в том, что, зная эти несколько знаков и правила их комбинации, можно записать практически любое число. Выучив их, вы получите ключ к пониманию всей римской нумерации.
| Римская цифра | Соответствующее арабское число |
|---|---|
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1000 |
Соответствие римских цифр с арабскими
Чтобы уверенно работать с римскими цифрами, нужно начать с малого — запомнить соответствие основных символов. Эти таблицы помогут быстро освоить нумерацию и переводить числа из одной системы в другую.
Римские цифры от 1 до 10
Это базовый набор цифр, который нужно знать наизусть. Он строится на принципах сложения и вычитания с помощью всего трех символов: I, V, X.
Римские цифры от 1 до 20
Продолжаем изучать числа, добавляя к первому десятку второй. Здесь закрепляется принцип сложения.
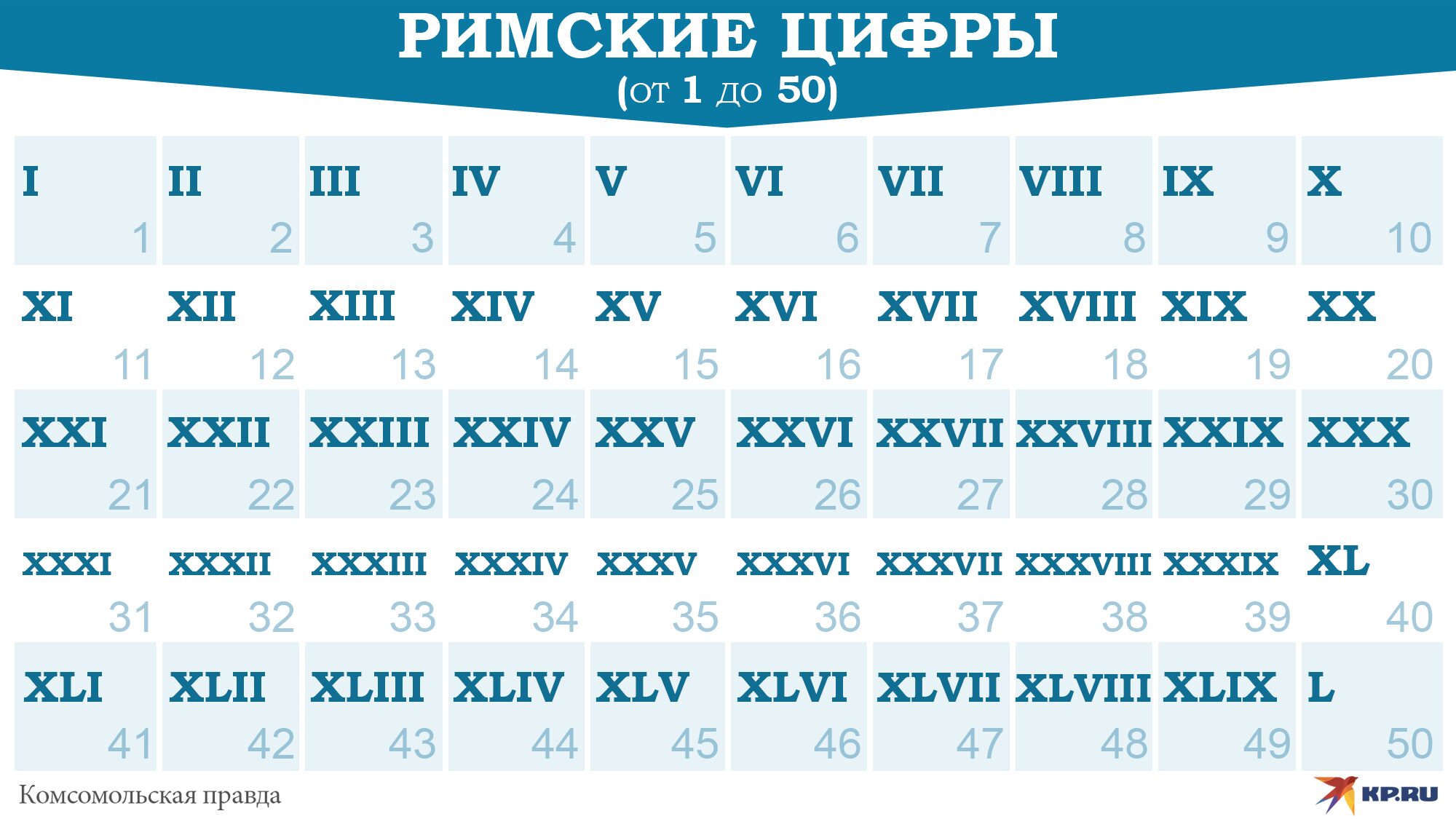
Римские цифры от 1 до 50
На этом этапе добавляется новый символ — L, а также числа, использующие X и L вместе. Это расширенная таблица для тех, кто хочет глубже понять систему.
Правила записи римских цифр
Запись чисел в римской системе подчиняется двум фундаментальным правилам: принципу сложения и принципу вычитания. Эти законы формируют уникальный числовой язык, где значение цифры зависит от ее позиции относительно соседей. Разберем каждый принцип детально.
Принцип сложения в системе римских цифр
Основное правило гласит: если цифра, обозначающая меньшее значение, стоит после цифры с большим значением, то их величины складываются. Этот принцип является основой для построения большинства чисел.
Примеры перевода
Покажем на примерах:
VI = V + I = 5 + 1 = 6
XII = X + I + I = 10 + 1 + 1 = 12
LX = L + X = 50 + 10 = 60
MDC = M + D + C = 1000 + 500 + 100 = 1600
Принцип вычитания в системе римских цифр
Обратное правило: если цифра, обозначающая меньшее значение, стоит перед цифрой с большим значением, то ее величина вычитается. Этот принцип позволяет лаконично записывать числа, близкие к новому разряду.
Примеры перевода
Вот как переводить римские цифры в арабские с помощью принципа вычитания:
IV = V — I = 5 — 1 = 4
IX = X — I = 10 — 1 = 9
XL = L — X = 50 — 10 = 40
XC = C — X = 100 — 10 = 90
CD = D — C = 500 — 100 = 400
CM = M — C = 1000 — 100 = 900
это интересно
Ограничения в системе римских цифр
Чтобы избежать неоднозначности, в системе действуют строгие ограничения.
- Запрет на нестандартное вычитание: вычитать можно только из двух ближайших по номиналу старших цифр.
- Запрет на четверное повторение: одна и та же цифра не может повторяться подряд более трех раз.
Примеры ограничений
Сравните верный и неверный перевод.
Неверно: IC (100 — 1) для числа 99.
Верно: XCIX = (100 — 10) + (10 — 1) = 90 + 9 = 99.
Неверно: IIII для числа 4.
Верно: IV = 4.
Задачи по теме «Римские цифры»
Проверим, как вы усвоили материал. Переведите римские цифры в арабские и наоборот. Сначала попробуйте решить самостоятельно, а потом сверьтесь с ответами.
Задача 1
Запишите арабскими цифрами:
а) VIII
б) XIV
в) XIX
г) XL
Задача 2
Запишите римскими цифрами:
а) 7
б) 15
в) 24
г) 49
Задача 3
Прочитайте год, указанный на фасаде старого здания: MDCCCXLII.
Задача 4
Исправьте ошибку в записи числа: 95 записано как VC.
Ответы к задачам
Ответы и решения для каждой задачи представлены ниже. Обязательно проверьте себя.
Задача 1
а) VIII = 5 + 1 + 1 + 1 = 8
б) XIV = 10 + (5 — 1) = 10 + 4 = 14
в) XIX = 10 + (10 — 1) = 10 + 9 = 19
г) XL = 50 — 10 = 40
Ответ: а) 8; б) 14; в) 19; г) 40
Задача 2
а) 7 = 5 + 1 + 1 = VII
б) 15 = 10 + 5 = XV
в) 24 = 10 + 10 + (5 — 1) = XXIV
г) 49 = (50 — 10) + (10 — 1) = XLIX
Ответ: а) VII; б) XV; в) XXIV; г) XLIX
Задача 3
Разбиваем число на части: MDCCCXLII = M + D + CCC + XL + II.
Переводим: 1000 + 500 + 300 + 40 + 2 = 1842.
Ответ: 1842 год
Задача 4
Запись числа 95 как VC не соответствует правилам, так как вычитать можно только из ближайших старших цифр (из L или C, но не из V). Правильная запись: XCV = (100 — 10) + 5 = 90 + 5 = 95.
Ответ: XCV
Популярные вопросы и ответы
Отвечает Анна Жадан, старший преподаватель математики, методист Домашней школы «ИнтернетУрок»:
Почему в римских цифрах отсутствует ноль?
С помощью цифр древние римляне фиксировали количество предметов или событий, поэтому запись числа 0 как такового была не нужна. Для того чтобы обозначить отсутствие чего-либо, использовалось понятие nulla, «ничто», или «нет». Использовать дополнительный символ, означающий 0, для запись других чисел было нецелесообразно.
Римская система счисления не является позиционной, числа в ней записываются посредством сочетания символов с правилами сложения и вычитания, поэтому ноль для представления пустой позиции не нужен.
Римская система счисления не является позиционной, числа в ней записываются посредством сочетания символов с правилами сложения и вычитания, поэтому ноль для представления пустой позиции не нужен.
Как записать дату римскими цифрами?
Записать дату римскими цифрами можно для дня, месяца и года, используя соответствующие римские цифры. День записывается как число от 1 до 31 в римской записи, месяц — номер месяца в римской системе: I — январь, II — февраль и XII — декабрь. Год записывается как обычное число в римской системе счисления. Например, «3 января 2025 года» запишется как III.I.MMXXV.
Почему тему по математике «Римские цифры» изучают уже во 2-4 классах?
В начальной школе дети начинают знакомиться с понятиями чисел и различных систем счисления. Помимо используемой в современном мире десятичной системы счисления, важно познакомить школьников и с другими вариантами записи чисел. Изучение римских цифр развивает понимание числовых различных операций с числами, таких как сумма и разность, учит работать с непрерывной шкалой без строгой десятичной позиции. Кроме того, римские цифры встречаются в архитектуре, на изображениях на старинных монетах, на часах и в названиях монументов. Знание римских цифр помогает ориентироваться в повседневной реальности и понимать культурное наследие.
В каких заданиях ОГЭ и ЕГЭ проверяется навык решения задач по теме «Римские цифры»?
Тема «Римские цифры» изучается в школе, но не встречается в ОГЭ и ЕГЭ напрямую. Несмотря на это, тема является важной для изучения, поскольку формирует фундаментальное логическое и историко-математическое мышление, необходимое для решения более сложных задач.
