Синус, косинус, тангенс, котангенс угла: что такое, таблица основных значений, свойства, примеры, задачи с ответами по геометрии для 7, 8, 9, 10, 11 классов и подготовки к ЕГЭ по математике

Тригонометрия окружает нас повсюду — от строительства зданий до программирования игр. Ее основа — четыре ключевые функции: синус, косинус, тангенс и котангенс. Они связывают углы с соотношениями сторон в треугольниках, а их графики описывают волны, колебания и циклы.

У каждой функции — свои свойства и особенности. Разберемся, как их вычислять, запоминать и применять в реальных задачах.

Полезная информация о синусе, косинусе, тангенсе, котангенсе

Каждая тригонометрическая функция обладает уникальным набором свойств, определяющих ее поведение и область применения. Систематизация этих характеристик помогает в решении практических задач.

Синус, косинус, тангенс, котангенс	Объяснение
Область определения	sin x, cos x определены для всех x∈R tg x определен при x ≠ π/2 + πn ctg x определен при x ≠ πn
Область значений	sin x ∈ [-1;1] cos x ∈ [-1;1] tg x ∈ (-∞;+∞) ctg x ∈ (-∞;+∞)
Периодичность	sin x, cos x имеют период 2π tg x, ctg x имеют период π
Четность	cos x — четная функцияsin x, tg x, ctg x — нечетные функции
Основное тождество	sin²x + cos²x = 1
Взаимосвязи	tg x = sin x / cos x ctg x = cos x / sin x ctg x = 1 / tg x

Что такое синус в математике

Синус представляет собой одну из основных тригонометрических функций, связывающую острый угол с отношением сторон прямоугольного треугольника. Синус угла равен отношению длины противолежащего катета к длине гипотенузы:

\(\sin\;A\;=\;\frac{\;противолежащий\;катет}{гипотенуза}\)

Синус, косинус, тангенс, котангенс угла — Синус угла, определенный через прямоугольный треугольник. Изображение: Ирина Соколова

Для любого угла синус можно определить с помощью единичной окружности. Для этого поместим центр окружности с радиусом, равным 1, в начало координат. Отложим угол α от положительного направления оси абсцисс (OX). Точка P пересечения луча с окружностью имеет координаты (x; y), где:

sin α = y

Разберемся, почему так происходит. Если опустить перпендикуляр из точки P на ось абсцисс, получится прямоугольный треугольник OPH, где:

гипотенуза OP равна 1, так как является радиусом окружности;
катет PH, противолежащий углу α, соответствует координате y точки P;
катет OH, прилежащий к углу α, соответствует координате x точки P.

Из определения синуса в прямоугольном треугольнике:

\(\sin\;\alpha\;=\frac{\;PH}{OP}\;=\;\frac{\;y}1\;=\;y\)

Таким образом, синус угла на единичной окружности численно равен ординате соответствующей точки.

Что такое косинус в математике

Косинус, как и синус, является важнейшей тригонометрической функцией, которая устанавливает зависимость между углами и сторонами прямоугольного треугольника. В прямоугольном треугольнике косинус острого угла определяется как отношение прилежащего к этому углу катета к гипотенузе:

\(\cos\;A\;=\;\frac{прилежащий\;катет}{гипотенуза}\)

Для произвольного угла косинус удобно определять через единичную окружность. Рассмотрим окружность радиуса 1 с центром в начале координат. Если отложить угол α от положительного направления оси OX, то точка пересечения конечной стороны угла с окружностью будет иметь координаты (x; y), где:

cos α = x

Это соотношение легко объяснить. Опустим перпендикуляр из точки P на ось OX. Получившийся прямоугольный треугольник OPH обладает следующими характеристиками:

гипотенуза OP равна 1, так как является радиусом окружности;
катет OH, прилежащий к углу α, соответствует координате x точки P;
катет PH, противолежащий углу α, соответствует координате y точки P.

Согласно определению косинуса для прямоугольного треугольника:

\(\cos\;\alpha\;=\;\frac{OH}{OP}\;=\;\frac x1\;=\;x\)

Таким образом, косинус угла на единичной окружности численно равен абсциссе соответствующей точки.

Что такое тангенс в математике

Тангенс также является важной тригонометрической функцией, которую можно рассмотреть через прямоугольный треугольник.

Тангенс угла равен отношению длины противолежащего катета к длине прилежащего катета:

\(tg\;A\;=\;\frac{противолежащий\;катет}{прилежащий\;катет}\)

Для любого угла тангенс можно определить через единичную окружность. Рассмотрим окружность радиуса 1 с центром в начале координат. Отложим угол α от положительного направления оси OX. Точка P пересечения луча с окружностью имеет координаты (x; y), где:

\(tg\;\alpha\;=\;\frac yx\)

Разберемся, почему это так. Опустим перпендикуляр из P на ось OX, получив прямоугольный треугольник OPH. В этом треугольнике:

гипотенуза OP равна 1, так как является радиусом окружности;
катет PH, противолежащий углу α, соответствует координате y точки P;
катет OH, прилежащий к углу α, соответствует координате x точки P.

Из определения тангенса в прямоугольном треугольнике:

\(tg\;\alpha\;=\;\frac{PH}{OH}\;=\;\frac yx\)

Что такое котангенс в математике

Котангенс является важной тригонометрической функцией, дополняющей тангенс. В прямоугольном треугольнике котангенс острого угла определяется как отношение прилежащего катета к противолежащему:

\(ctg\;A\;=\;\frac{прилежащий\;катет}{противолежащий\;катет}\)

Для произвольного угла котангенс можно выразить через координаты на единичной окружности. Возьмем окружность радиуса 1 с центром в начале координат. Отложим угол α от оси OX. Точка P пересечения с окружностью имеет координаты (x; y), где:

\(ctg\;\alpha\;=\;\frac xy\)

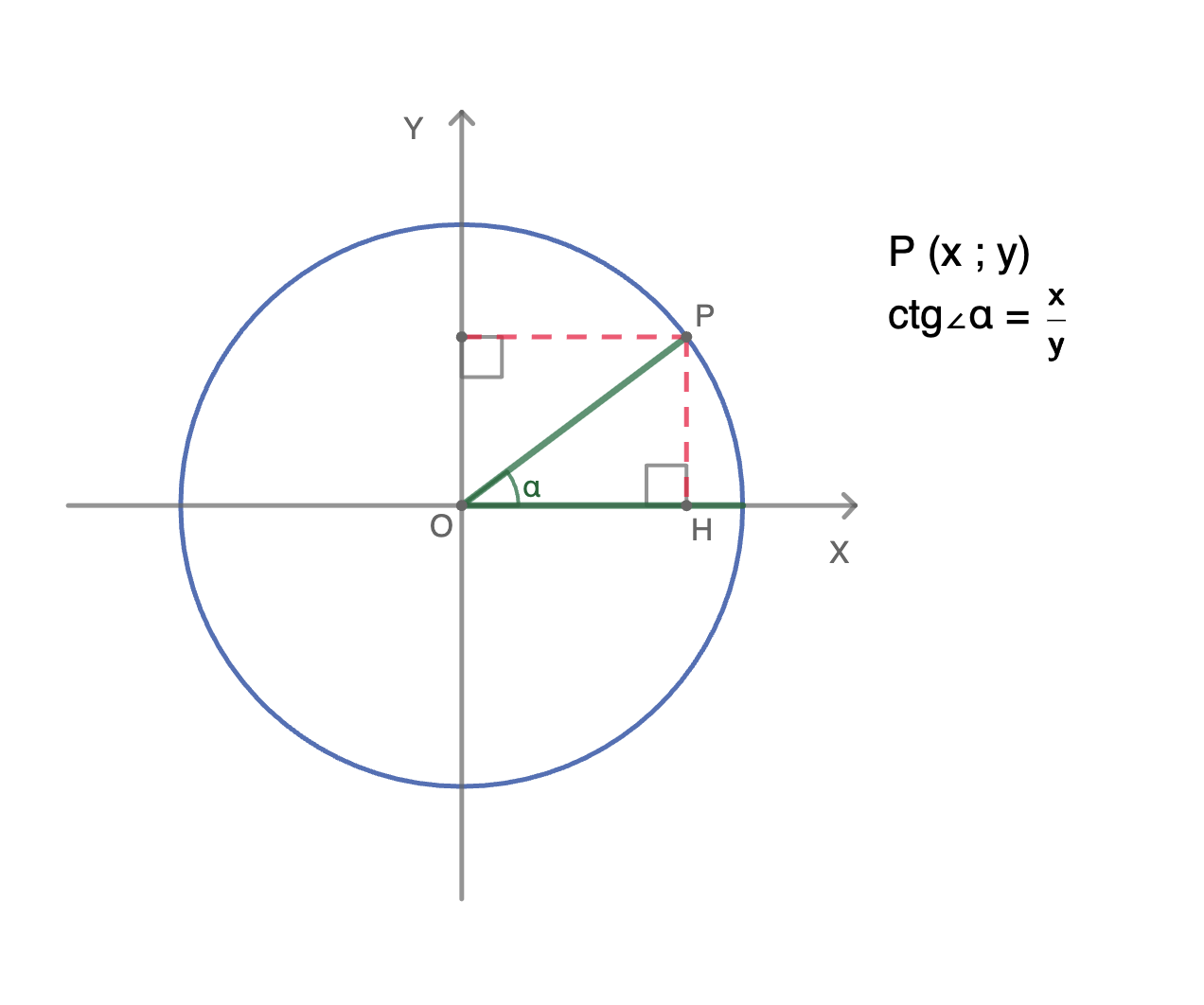
Это соотношение объясняется через построение прямоугольного треугольника OPH, где из точки P опущен перпендикуляр PH:

гипотенуза OP равна 1, так как является радиусом окружности;
катет OH, прилежащий к углу α, соответствует координате x точки P;
катет PH, противолежащий углу α, соответствует координате y точки P.

\(ctg\;\alpha\;=\;\frac{OH}{PH}\;=\;\frac xy\)

Обратите внимание, что котангенс является обратной величиной к тангенсу:

\(ctg\;\alpha\;=\;\frac1{tg\;\alpha}1\)

Таблица основных значений синусов, косинусов, тангенсов и котангенсов

Из определений тригонометрических функций на единичной окружности мы можем сделать важные выводы о природе этих функций и их свойствах.

На единичной окружности четко обозначены две особые оси:

ось синусов — вертикальная ось OY (ось ординат);
ось косинусов — горизонтальная ось OX (ось абсцисс).

Но что же с тангенсом и котангенсом? У них тоже есть свои особые оси, расположенные вне самой окружности:

ось тангенсов — вертикальная прямая, проходящая через точку (1,0);
ось котангенсов — горизонтальная прямая, проходящая через точку (0,1).

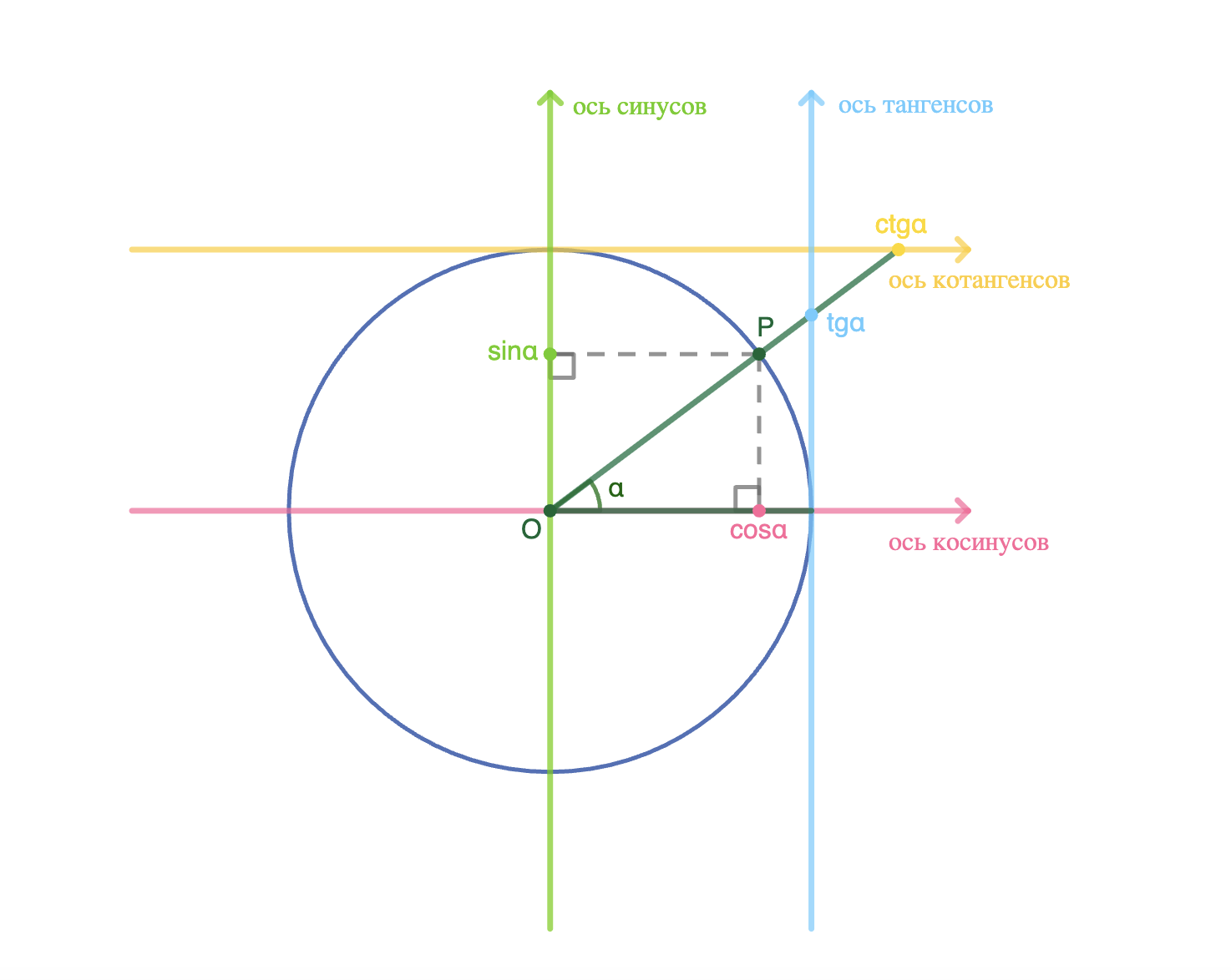
Это расположение осей объясняет принципиальную разницу в поведении функций. Синус и косинус ограничены значениями от -1 до 1, так как их оси ограничены самой окружностью. Тангенс и котангенс могут принимать любые значения от -∞ до +∞, так как их оси выходят за пределы окружности.

Мы уже сказали, что значения синуса и косинуса угла находятся через координаты точки пересечения луча и окружности, а тангенс и котангенс — как отношения этих координат. Но также тангенс и котангенс можно находить при помощи точки пересечения луча с их осями. Тогда значение тангенса будет равно у-координате точки пересечения с осью тангенсов, значение котангенса будет равно x-координате точки пересечения с осью котангенсов.

Исходя из таких деталей мы сразу можем определить, какой знак будет у значений тригонометрических функций для разных углов в разных четвертях окружности.

Помимо знака тригонометрической функции мы можем узнать и само значение, выведя его через прямоугольный треугольник и проекции на оси. Но выводить каждый раз необязательно — для этого существует таблица основных значений тригонометрических функций для разных углов.

Зная таблицу основных значений, можно определять значения и других углов, используя свойства тригонометрических функций.

Обратите внимание, что углы могут измеряться не только градусной мерой, но и в радианах, где: π рад = 180°.

Для перевода из градусов в радианы используем формулу:

\(\frac{градусы\;\times\;\pi}{180^\circ}\;=\;радианы\)

Для перевода из радиан в градусы используем формулу:

\(\frac{радианы\;\times\;180^\circ}\pi\;=\;градусы\)

Эта система измерения особенно удобна при работе с тригонометрическими функциями, так как многие формулы в радианах выглядят проще и естественнее.

Свойства синуса, косинуса, тангенса, котангенса

Тригонометрические функции обладают рядом фундаментальных свойств, которые определяют их поведение и взаимосвязи. Эти свойства позволяют нам решать сложные математические задачи.

Область определения

Все тригонометрические функции определены для произвольных углов, но имеют особенности:

sin α и cos α: определены для всех действительных чисел α ∈ R;
tg α: не существует при α = π/2 + πn (n ∈ Z) — когда косинус равен нулю;
ctg α: не существует при α = πn (n ∈ Z) — когда синус равен нулю.

Область значений

Функции различаются по возможным значениям:

sin α и cos α: принимают значения строго от -1 до 1 включительно;
tg α и ctg α: могут принимать любые действительные значения.

Периодичность

Все тригонометрические функции периодичны:

sin α и cos α: период 2π (360°),
tg α и ctg α: период π (180°).

Это означает, что их значения полностью повторяются через указанный интервал.

это интересно

20+ лучших онлайн-курсов ЕГЭ по математике

Какие курсы ЕГЭ по математике помогут получить высшую оценку

Подробнее

Четность и нечетность

Четность функции означает, что ее значение не изменяется при замене аргумента α на противоположное значение, нечетность функции показывает, что при изменении знака аргумента значение функции также меняет знак. Так, cos α — четная функция: cos(-α) = cos α. А sin α, tg α, ctg α — нечетные функции: sin(-α) = -sin α, tg(-α) = -tg α, ctg(-α) = -ctg α.

Основные тождества

Существуют фундаментальные соотношения, которые связывают различные тригонометрические функции между собой.

Основное тригонометрическое тождество: sin²α + cos²α = 1

Помимо основного тождества есть еще несколько, которые показывают взаимосвязь между функциями:

tg α = sin α / cos α
ctg α = cos α / sin α
tg α · ctg α = 1

Задачи по теме «Синус, косинус, тангенс, котангенс угла»

Решим несколько типовых задач на тригонометрические функции. Эти задания помогут вам научиться работать с единичной окружностью и функциями, а также потренироваться с преобразованиями.

Задача 1

В прямоугольном треугольнике один из катетов равен 3, а гипотенуза равна 5. Найдите синус, косинус и тангенс острого угла, противолежащего данному катету.

Задача 2

Найдите значение выражения: 2sin30° + 3cos60° — tg45°.

Задача 3

Найдите tgα, если

\(\sin\alpha\;=\;\frac5{13}\;и\;\alpha\;\in\;(\frac\pi2;\;\pi)\)

Задача 4

Упростите выражение:

\(\frac{(\sin²\alpha\;-\;1)}{(1\;-\;\cos²\alpha)}\;+\;ctg\alpha\;\times\;\sin\alpha.\)

Ответы к задачам

Ниже приведено подробное решение каждой задачи. Обязательно проверьте себя.

Задача 1

Обозначим известный катет треугольника за a = 3, гипотенузу — с = 5. Найдем неизвестный катет b через теорему Пифагора:

b² = c² — a² = 5² — 3² = 25 — 9 = 16

b = 4

Теперь найдем синус, косинус и тангенс острого угла:

\(\sin\;A\;=\;\frac ac\;=\;\frac35\;=\;0,6\\\\\cos\;A\;=\;\frac bc\;=\;\frac45\;=\;0,8\\\\tg\;A\;=\;\frac ab\;=\;\frac34\;=\;0,75\\\\\)

Ответ: 0,6; 0,8; 0,75

Задача 2

Из таблицы основных значений тригонометрических функций мы знаем, что

\(\sin30^\circ\;=\;\frac12\;,\;\cos60^\circ\;=\;\frac12\;,\;tg45^\circ\;=\;1.\)

Найдем значение выражения:

\(2\sin30^\circ+3\cos60^\circ-tg45^\circ=\;2\times\frac12+\;3\times\frac12-1=1+1,5-1=1,5\)

Ответ: 1,5

Задача 3

Зная значение синуса угла, мы можем найти значение косинуса через основное тригонометрическое тождество:

\(\sin^2\alpha\;+\;\cos^2\alpha\;=\;1\\\;\;\\\cos^2\alpha\;=\;1\;-\;\sin^2\alpha\\\;\;\\\cos^2\alpha\;=\;1\;-\;{(\frac5{13})}^2\;=\;1\;-\;\frac{25}{169}\;=\;\frac{144}{169}\\\;\;\\Тогда\;\cos\;\alpha\;=\;\frac{12}{13}\;или\;\cos\;\alpha\;=\;-\frac{12}{13}\\\)

Также мы знаем о связи тангенса с синусом и косинусом угла:

\(tg\;\alpha\;=\;\frac{\sin\;\alpha}{\cos\;\alpha\;}\\\\\\\\tg\;\alpha\;=\;(\frac5{13})\;:\;(-\frac{12}{13})\;=\;-\frac5{12}\\\)

\(Ответ:\;-\frac5{12}\)

Задача 4

Будем делать преобразования функций с помощью основных тождеств:

\(\frac{(\sin^2\alpha\;-\;1)}{(1\;-\;\cos^2\alpha)}+\;ctg\alpha\times\sin\alpha\;=\frac{(\sin^2\alpha\;-\;1)}{(1\;-\;(1\;-\;\sin^2\alpha))}+\;(\frac{\cos\alpha}{\sin\alpha})\times\sin\alpha\;=\\\\=\frac{\;(\sin^2\alpha\;-\;1)}{(1\;-\;1\;+\;\sin^2\alpha)}+\;\cos\alpha=\frac{(\sin^2\alpha\;-\;1)}{\sin^2\alpha}+\;\cos\alpha=\\\\=-\frac{\;(1\;-\;\sin^2\alpha)}{\sin^2\alpha}+\;\cos\alpha=-\frac{\cos^2\alpha}{\sin^2\alpha}+\cos\alpha=\\\\=-ctg^2\alpha+\;\cos\alpha=\;\cos\alpha-ctg^2\alpha\\\\\;\;\)

Ответ: cosα — ctg²α

Синус, косинус, тангенс, котангенс угла