Векторы в математике
Разберемся, что такое векторы в математике, где они применяются и как с их помощью решать практические задачи по алгебре, геометрии и физике
Представьте, что вы зовете друга на встречу и вам нужно не просто сказать «кафе находится в 300 метрах от дома», а точно указать направление: «кафе находится в 300 метрах на северо-восток». В математике для таких ситуаций существуют векторы. Это инструмент, который позволяют одновременно учитывать и величину, и направление.
Мы сталкиваемся с векторами ежедневно, даже не задумываясь об этом. Когда вы бросаете мяч другу, его полет описывается вектором – у него есть и скорость, и направление. Ветер, дующий с определенной силой в сторону вашего дома, автомобиль, поворачивающий на перекрестке, – все эти явления можно описать с помощью векторов. В физике они помогают рассчитывать силы, в географии – строить маршруты, а в компьютерных играх – создавать реалистичное движение персонажей.
Что такое векторы в математике
Вектор – это направленный отрезок, у которого есть длина и направление. Этот отрезок обязательно имеет начало и конец, что делает его похожим на стрелку.
Векторы обозначают двумя способами:
\(\cdot\;строчной\;буквой\;со\;стрелочкой\;сверху\;-\;\overset\rightharpoonup a\;\;\\\cdot двумя\;заглавными\;буква\;со\;стрелочкой\;сверху\;-\;\overrightarrow{AB},\;где\;A\;–\\\;начало\;вектора,\;B\;–\;конец\;вектора.\)
\(Важно\;в\;названии\;вектора\;не\;перепутать\;буквы\;местами,\;\\иначе\;получится\;совсем\;другой\;вектор\;–\;\overrightarrow{BA},\;он\;такой\;\\же\;длины,\;но\;направленный\;в\;обратную\;сторону.\;\)
Полезная информация о векторах в математике
Векторы – непростая тема, но важная. Чтобы легко разбираться в задачах, сохраните эту таблицу-шпаргалку. В ней собраны все основные понятия о векторах – от простых обозначений до важных свойств, которые пригодятся вам.
| Термин | Определение векторов |
|---|---|
| Вектор | направленный отрезок |
| Длина вектора | расстояние между началом и концом вектора |
| Нулевой вектор | вектор с длиной 0, начало и конец совпадают |
| Единичный вектор | вектор с длиной 1, используется для указания направления |
| Коллинеарные векторы |  – лежат на параллельных прямых или на одной прямой |
| Сонаправленные векторы |  – коллинеарные векторы, направленные одинаково |
| Противоположно направленные векторы |  – коллинеарные векторы, противоположные по направлению |
Виды векторов в математике
Векторы можно классифицировать по нескольким ключевым признакам, которые определяют их свойства и возможности применения в различных задачах. Основные различия между векторами проявляются в их длине и направлении, взаимном расположении относительно друг друга, а также особых математических характеристиках.
По взаимному расположению векторы бывают коллинеарными и неколлинеарными. По направлению мы различаем сонаправленные и противоположно направленные векторы. Отдельно выделяются векторы с особыми свойствами: единичные, нулевые, равные и противоположные. Подробно разберем каждый из этих видов.
Коллинеарные и неколлинеарные векторы
Все векторы делятся на два принципиально разных типа:
- коллинеарные векторы – лежат на одной прямой или на параллельных прямых.
- неколлинеарные векторы – не являются коллинеарными.
\(На\;рисунке\;видно,\;что\;векторы\;\overrightarrow a\;и\;\overrightarrow b\;являются\;коллинеарными\\относительно\;друг\;друга,\;так\;как\;лежат\;на\;параллельных\;\\прямых,\;а\;также\;векторы\;\overrightarrow k\;и\;\overrightarrow d,\;потому\;что\;лежат\;на\;\\одной\;прямой.\;Пары\;векторов\;\overrightarrow m\;и\;\overrightarrow n,\;\overrightarrow x\;и\;\overrightarrow y\;неколлинеарны\\относительно\;друг\;друга.\)
\(Коллинеарные\;векторы\;можно\;обозначить\;так:\;\overrightarrow a\parallel\overrightarrow b.\)
Сонаправленные и противоположно направленные векторы
Коллинеарные векторы можно разделить, в свою очередь, на два типа в зависимости от направления:
- сонаправленные – направлены в одну сторону;
- противоположно направленные – направлены в разные стороны.
\(На\;рисунке\;векторы\;\overrightarrow a\;и\;\overrightarrow b,\;\overrightarrow f\;и\;\overrightarrow e\;сонаправлены\;между\\\;собой.\;Векторы\;\overrightarrow m\;и\;\overrightarrow n,\;\overrightarrow x\;и\;\overrightarrow y\;противоположно\;\\направлены.\;\)
Сонаправленные векторы обозначаются так:
Равные векторы
Очень большое значение имеет понятие равенства векторов. Важно понимать, что это не просто совпадение длин отрезков.
\(Равные\;векторы\;сонаправлены\;и\;имеют\;равные\;длины.\;\\Записывается\;это\;так:\;\overrightarrow a\;=\;\overrightarrow b.\)
Противоположные векторы
\(Противоположные\;векторы\;противоположно\;направлены,\;\\при\;этом\;имеют\;равную\;длину.\;Если\;\overrightarrow a\;–\;произвольный\;\\вектор,\;то\;противоположный\;ему\;вектор\;записывается\;\\как\;-\overrightarrow a.\)
Нулевой вектор
В векторном мире нулевой вектор занимает особое положение, аналогичное нулю в обычной арифметике.
Нулевой вектор определяется как вектор с нулевой длиной, у которого начало и конец совпадают. Его направление считается неопределенным, а в координатном представлении все его компоненты равны нулю. Он считается коллинеарным любому вектору.
\(Обозначается\;как\;\overrightarrow0.\)
Единичный вектор
Зачастую в задачах мы сталкиваемся с понятием единичного вектора. Это базовый элемент для описания направлений.
Единичный вектор – это вектор, длина которого равна единице. Его можно получить из любого ненулевого вектора, разделив этот вектор на его собственную длину.
\(Математически\;это\;записывается\;так:\;\overrightarrow e\;=\;\frac{\overrightarrow a}{\left|\overrightarrow a\right|}\)
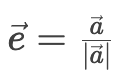
Сложение векторов
Сложение векторов – это операция, в результате которой получается новый вектор, называемый суммой векторов. Существует три основных способа сложения, удобных в разных ситуациях.
Правило треугольника
Правило треугольника является наиболее интуитивно понятным способом сложения двух векторов. Его суть заключается в последовательном откладывании векторов: начало второго вектора совмещается с концом первого. При этом результирующий вектор проводится от начала первого вектора к концу второго.
Правило параллелограмма
Для случаев, когда два вектора выходят из одной точки, чаще применяют правило параллелограмма. В этом методе оба вектора откладываются из общего начала, на них строится параллелограмм, и искомая сумма совпадает с диагональю этого параллелограмма.
Правило многоугольника
Когда требуется сложить три и более векторов, наиболее универсальным становится правило многоугольника. Этот метод является естественным обобщением правила треугольника: все векторы последовательно соединяются «конец к началу», а суммарный вектор замыкает полученную ломаную линию, соединяя начало первого вектора с концом последнего.
Сложение векторов подчиняется тем же привычным правилам, что и обычное сложение чисел, но с учетом направления:
\(\cdot\;\overrightarrow a\;+\;\overrightarrow b\;=\;\overrightarrow b\;+\;\overrightarrow a\;–\;переместительный\;закон,\;\;\\\cdot\;(\overrightarrow a\;+\;\overrightarrow b)\;+\;\overrightarrow c\;=\;\overrightarrow a\;+\;(\overrightarrow b\;+\;\overrightarrow c)\;–\;сочетательный\;закон,\\\cdot\;\overrightarrow a\;+\;\overrightarrow0\;=\;\overrightarrow a\;–\;сложение\;с\;нулевым\;вектором,\;\\\cdot\;\overrightarrow a\;+\;(-\overrightarrow a)\;=\;\overrightarrow0\;–\;сложение\;противоположных\;векторов.\)
Вычитание векторов
Вычитание вектора равносильно сложению с противоположным вектором:
\(\overrightarrow a\;-\;\overrightarrow b\;=\;\overrightarrow a\;+\;(-\overrightarrow b),\;\;где\;-\overrightarrow b\;–\;вектор,\;\\противоположный\;\overrightarrow b,\;то\;есть\;такой\;же\;длины,\;\\но\;противоположного\;направления.\)
Тогда при решении находим вектор, противоположный вычитаемому, а далее складываем векторы по правилу треугольника или параллелограмма.
Рассмотрим еще один, более наглядный способ вычитания векторов. Откладываем оба вектора из одной начальной точки. Вектор разности соединяет конец вычитаемого вектора с концом уменьшаемого. Этот способ позволяет не использовать дополнительно сложение векторов, а сразу находить их разность.
Умножение вектора на число
При умножении вектора на любое число k мы всегда получаем вектор, коллинеарный исходному. Значение k влияет на направление полученного вектора и на его длину.
Рассмотрим три ситуации:
- k > 0 – вектор сохраняет направление (сонаправленный исходному);
- k = 0 – получаем нулевой вектор;
- k < 0 – вектор меняет направление (противоположно направленный исходному).
\(При\;умножении\;вектора\;\overrightarrow a\;на\;число\;k\;длина\;вектора\\\;изменяется\;в\;\vert k\vert\;раз:\;\;\vert k\overrightarrow a\vert\;=\;\vert k\vert\times\vert\overrightarrow a\vert,\)
тогда при:
|k|>1 – вектор растягивается,
|k|<1 – вектор сжимается.
Координаты вектора на плоскости и в пространстве
Векторы можно точно описать с помощью чисел – координат. Это позволяет перевести геометрические задачи в алгебраические вычисления.
\(На\;плоскости,\;то\;есть\;в\;двумерном\;пространстве,\;\\вектор\;задается\;двумя\;координатами:\;\overrightarrow a\;=\;(a_x;\;a_y),\)
гду ax – проекция на ось OX, ay – проекция на ось OY.
Если известны точки начала A(x1; y1) и конца B(x2; y2):
\(\overrightarrow{AB}\;=\;(x_2-x_1;\;y_2-y_1)\)
\(В\;пространстве\;для\;векторов\;добавляется\;третья\;\\координата:\;\overrightarrow b\;=\;(b_x;\;b_y;\;b_z),\;где\;b_x\;–\;проекция\;на\;ось\;OX,\;\\b_y\;–\;проекция\;на\;ось\;OY,\;b_z\;–\;проекция\;на\;ось\;OZ.\)
Аналогично, как и на плоскости, если известны точки начала A(x1; y1; z1) и конца B(x2; y2; z2):
\(\overrightarrow{AB}\;=\;(x_2-x_1;\;y_2-y_1;\;z_2-z_1)\)
Действия с векторами в координатной форме
\(Когда\;векторы\;заданы\;координатами\;\overrightarrow a\;=\;(a_x;\;a_y),\;\\\overrightarrow b\;=\;(b_x;\;b_y),\;все\;операции\;с\;ними\;выполняются\;просто\;и\\\;наглядно\;–\;покоординатно.\;Рассмотрим\;основные\;действия,\;\\которые\;помогут\;вам\;легко\;решать\;задачи.\;\)
\(1.\:Сложение\;векторов:\;\overrightarrow a\;+\;\overrightarrow b\;=\;(a_x+b_x;\;a_y+b_y).\;\;\\2.\:Вычитание\;векторов:\;\overrightarrow a\;-\;\overrightarrow b\;=\;(a_x-b_x;\;a_y-b_y).\;\;\\3.\:Умножение\;вектора\;на\;число:\;k\overrightarrow a\;=\;(ka_x;\;ka_y).\)
это интересно
Основное тригонометрическое тождество
Что такое основное тригонометрическое тождество и как его использовать
Подробнее
Длина вектора
Длина вектора, или модуль, – это числовая характеристика, показывающая «размер» вектора независимо от его направления. Геометрически это расстояние между начальной и конечной точками вектора.
Если вектор уже задан координатами (ax; ay), то его длина находится по формуле:
\(\left|\overrightarrow a\right|\;=\;\sqrt{a_x^2\;+\;a_y^2}\)
Если известны координаты начала A(x1; y1) и конца B(x2; y2) вектора, то найти его длину можно по формуле:
\(\left|\overrightarrow{AB}\right|\;=\;\sqrt{{(x_1-x_2)}^2\;+\;{(y_1-y_2)}^2}\)
Или можно найти изначально координаты вектора, зная координаты начала и конца, а затем воспользоваться первой формулой.
Возможна ситуация, когда нам неизвестны координаты вектора и координаты его точек. Тогда мы можем воспользоваться теоремой косинусов:
\(\left|\overrightarrow с\right|\;=\;\sqrt{\left|\overrightarrow a\right|^2+\;\left|\overrightarrow b\right|^2-2\left|\overrightarrow a\right|\left|\overrightarrow b\right|\cos\alpha}\)
где α – угол между векторами.
Угол между векторами
В теореме косинусов для нахождения длины вектора нам встретилось понятие угла между векторами.
Угол между двумя векторами – это минимальный угол, на который нужно повернуть один вектор, чтобы его направление совпало с направлением другого вектора. Этот угол всегда находится в диапазоне от 0° до 180°.
Рассмотрим, как будет выглядеть угол между векторами:
Если один из векторов или оба являются нулевыми, то угол между ними 0°.
Скалярное произведение векторов
Скалярное произведение – это мощный инструмент, который позволяет не только вычислять углы между векторами, но и определять их взаимное расположение в пространстве. Разберемся, как находить скалярное произведение и как значение угла α влияет на результат этой операции.
\(Скалярное\;произведение\;векторов\;\overrightarrow a\;и\;\overrightarrow b\;вычисляется\;\\по\;формуле:\\\overrightarrow a\;\times\overrightarrow{\;b}\;=\;\left|\overrightarrow a\right|\;\times\;\left|\overrightarrow{\;b}\right|\;\times\;\cos\alpha\)
где α – угол между векторами.
\(Значение\;угла\;\alpha\;влияет\;на\;результат\;скалярного\;произведения.\;\\Так,\;если\;угол\;равен\;0^\circ,\;\cos\;0^\circ\;=\;1,\;произведение\;векторов\;\\максимально:\;\overrightarrow a\;\times\;\overrightarrow b=\;\left|\overrightarrow a\right|\;\times\;\left|\;\overrightarrow b\right|.\;Если\;угол\;равен\;90^\circ,\;\\\cos\;90^\circ=0,\;произведение\;векторов\;равно\;0:\;\overrightarrow a\;\times\;\overrightarrow b\;=\;0.\;\\Для\;значения\;угла\;180^\circ,\;\cos\;180^\circ\;=\;-1,\;произведение\;\\векторов\;минимально:\\\overrightarrow a\;\times\;\overrightarrow b=\;-\;\left|\overrightarrow a\right|\;\times\;\left|\;\overrightarrow b\right|\\\)
Соответственно, если угол острый, значение его косинуса положительно, произведение векторов тоже. Если угол тупой, то значение скалярного произведения отрицательно.
Из основного определения скалярного произведения можно выразить косинус угла между векторами:
\(\cos\alpha\;=\;\frac{\overrightarrow a\;\times\;\overrightarrow b}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}\)
\(Также\;если\;векторы\;представлены\;через\;координаты\;\\\overrightarrow a\;=\;(a_x;\;a_y),\;\overrightarrow b\;=\;(b_x;\;b_y),\;можно\;найти\;скалярное\;произведение\;\\координатным\;методом:\\\overrightarrow a\;\times\;\overrightarrow b\;=\;a_xb_x\;+\;a_yb_y\)
Задачи по теме «Векторы в математике»
Теперь, когда мы разобрали все основные понятия о векторах, давайте проверим, как вы можете применять эти знания на практике. Решите следующие задачи, используя изученные формулы и методы.
Задача 1
\(Даны\;векторы\;\overrightarrow a\;=\;(2;\;-3),\;\overrightarrow b\;=\;(-1;5).\;\\Найдите:\;\;\\1.\;\overrightarrow а\;+\;\overrightarrow b\;\;\\2.\;2\overrightarrow a\;-\;\overrightarrow b\)
Задача 2
\(Вычислите\;длину\;вектора\;\overrightarrow c\;=\;(6;\;-8).\)
Задача 3
\(Даны\;векторы\;\overrightarrow m\;=\;(1;\;0)\;и\;\overrightarrow n\;=\;(0;\;1).\;\\Найдите:\;\;\\1.\;скалярное\;произведение\;\overrightarrow m\;\times\;\overrightarrow n\;\;\\2.\;угол\;между\;этими\;векторами\)
Задача 4
\(Определите,\;являются\;ли\;векторы\;\overrightarrow d\;=\;(2;\;-1)\;и\\\overrightarrow p\;=\;(-6;\;3)\;коллинеарными.\;Ответ\;обоснуйте.\)
Задача 5
\(Точка\;A\;имеет\;координаты\;(1;2),\;точка\;B\;-\;(4;\;6).\;\\Найдите\;координаты\;вектора\;\overrightarrow{AB}\;и\;его\;длину.\)
Ответы к задачам
Проверьте свои решения и разберите подробные объяснения.
Задача 1
Выполним сложение, вычитание и умножение векторов в координатной форме:
\(1.\;\overrightarrow a\;+\;\overrightarrow b\;=\;(2+(-1);\;-3+5)\;=\;(1;\;2)\;\;\\2.\;2\overrightarrow a\;-\;\overrightarrow b\;=\;(2\times2-(-1);\;2\times(-3)-5)\;=\;(5;\;-11)\)
Ответ: (1; 2); (5; -11)
Задача 2
Вычислим длину вектора:
\(\vert\overrightarrow c\vert\;=\;\sqrt{6^2\;+\;(-8)^2}\;=\;\sqrt{36\;+\;64}\;=\;10\)
Ответ: 10
Задача 3
1. Найдем скалярное произведение координатным методом:
\(\overrightarrow m\;\times\;\overrightarrow n\;=\;1\;\times\;0\;+\;0\;\times\;1\;=\;0\;\)
2. Так как скалярное произведение равно 0, векторы перпендикулярны, угол между векторами равен 90°.
Ответ: 0; 90°
Задача 4
Векторы коллинеарны, так как их координаты пропорциональны.
2 / -6 = -1 / 3
Ответ: да, коллинеарны
Задача 5
\(Найдем\;координаты\;вектора\;\overrightarrow{AB}:\;\\\;\overrightarrow{AB}\;=\;(4-1;\;6-2)\;=\;(3;\;4)\;\;\\Найдем\;длину\;вектора\;\overrightarrow{AB}:\;\;\\\vert\overrightarrow{AB}\vert\;=\;\sqrt{32\;+\;42}\;=\;5\)
Ответ: (3;4); 5
Популярные вопросы и ответы
Отвечает Ольга Комарова, учитель математики:
Какой вектор называется нулевым?
Давайте разберемся с этим понятием по порядку. Для начала вспомним определение вектора: вектор – это направленный отрезок, у которого есть начало и конец. А теперь представьте, что будет, если начало и конец вектора – это одна и та же точка? Такой вектор назовем нулевым, его длина (модуль) равна 0. Направление у нулевого вектора не определено, но формально он может «смотреть» куда угодно.
Посмотрим, как в жизни будет выглядеть нулевой вектор. Если вы вышли из дома и вернулись обратно, то ваше перемещение – нулевой вектор. Вы переместились на 0 метров, и направление вашего движения не имеет значения.
Посмотрим, как в жизни будет выглядеть нулевой вектор. Если вы вышли из дома и вернулись обратно, то ваше перемещение – нулевой вектор. Вы переместились на 0 метров, и направление вашего движения не имеет значения.
Почему тему «Векторы» изучают в 9 классе?
Векторы появляются в программе 9 класса не случайно.
Давайте проверим, знаете ли вы ответы на вопросы:
1. Что такое отрезок и как обозначаются точки на плоскости?
2. Как решить уравнение 3x − 2 = 7?
3. Чему равна гипотенуза треугольника с катетами 3 и 4?
4. Как выглядит график функции y = 2x + 1?
Если да, то вы легко поймете тему векторов, но как раз все эти знания у вас будут приобретены к 9 классу. Наглядно покажу еще раз где и как.
Связь алгебры и геометрии. Векторы помогают «перевести» геометрические задачи на язык чисел. Например, с их помощью можно легко найти расстояние между точками или угол между прямыми.
Подготовка к физике. В 9 классе начинается серьезное изучение физики: сила, скорость, ускорение – все это векторы. Без понимания векторов сложно разбирать даже простые задачи на движение.
База для ЕГЭ и старшей школы. Векторы используются в стереометрии, тригонометрии, физике, экономике и даже в матанализе. Если не освоить их в 9 классе, потом будет сложно.
Развитие абстрактного мышления. Работа с векторами учит мыслить не только числами, но и работать с направлением – это важный шаг к более сложной математике.
Давайте проверим, знаете ли вы ответы на вопросы:
1. Что такое отрезок и как обозначаются точки на плоскости?
2. Как решить уравнение 3x − 2 = 7?
3. Чему равна гипотенуза треугольника с катетами 3 и 4?
4. Как выглядит график функции y = 2x + 1?
Если да, то вы легко поймете тему векторов, но как раз все эти знания у вас будут приобретены к 9 классу. Наглядно покажу еще раз где и как.
Связь алгебры и геометрии. Векторы помогают «перевести» геометрические задачи на язык чисел. Например, с их помощью можно легко найти расстояние между точками или угол между прямыми.
Подготовка к физике. В 9 классе начинается серьезное изучение физики: сила, скорость, ускорение – все это векторы. Без понимания векторов сложно разбирать даже простые задачи на движение.
База для ЕГЭ и старшей школы. Векторы используются в стереометрии, тригонометрии, физике, экономике и даже в матанализе. Если не освоить их в 9 классе, потом будет сложно.
Развитие абстрактного мышления. Работа с векторами учит мыслить не только числами, но и работать с направлением – это важный шаг к более сложной математике.
В каких заданиях ЕГЭ по математике понадобится знание темы «Векторы»?
Векторы встречаются в ЕГЭ профильного уровня. Во второй части они были практически всегда, а в первой появились в 2024 году. Вот конкретные задания, где они нужны: задание №2 первой части, задание №14 второй части, где векторы помогают решать задачи на расстояния и углы между прямыми и плоскостями; задание №17 второй части по планиметрии, где векторы упрощают доказательства в сложных геометрических задачах. Часто с помощью векторов (векторным методом) задача решается в несколько раз быстрее, чем классическим. Даже если в условии нет слова «вектор», их можно использовать для удобного решения.
