Координатная прямая
Разберемся, как устроена координатная прямая, научимся определять координаты точек и наоборот отмечать точки по координатам, а также освоим главное правило сравнения чисел с ее помощью
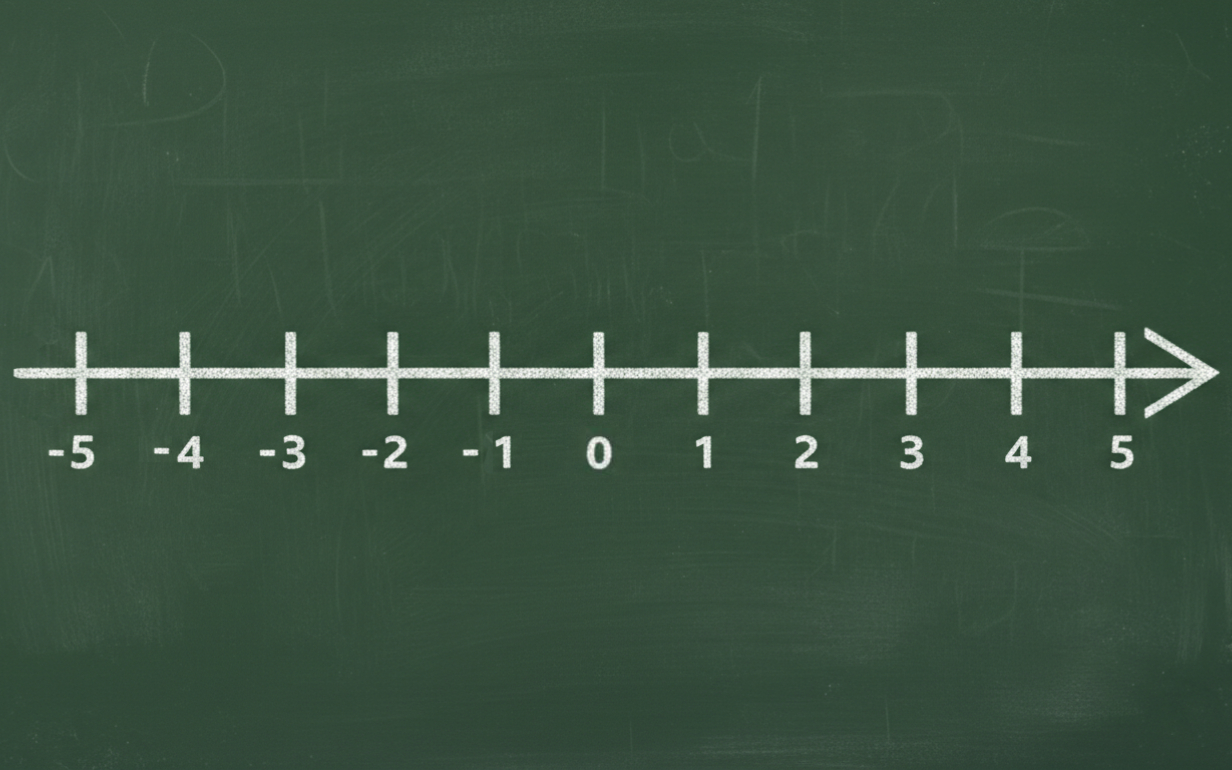
Представьте шкалу термометра. Ноль — это точка отсчета. Каждое деление отмеряет один градус, а числа выше и ниже нуля показывают не только величину температуры, но и ее изменение: движение вверх означает тепло, вниз — холод. Именно так работает координатная прямая. Это простейший и самый наглядный инструмент математики для упорядочивания чисел. Она превращает абстрактные числа в конкретные точки на линии, между которыми можно измерить расстояние и сразу увидеть, какое число больше, а какое меньше.
В этой статье вместе с преподавателем математики разберем, что такое координатная прямая и из каких элементов она состоит, научимся находить координаты точек и отмечать точки по заданным числам.
Что такое координатная прямая в математике
Координатная прямая, или числовая прямая, — это прямая, на которой установлено соответствие между всеми точками и действительными числами.
Иными словами, координатная прямая — это прямая, имеющая:
- начало отсчета,
- заданное направление,
- масштаб.
В результате любому действительному числу на такой прямой соответствует единственная точка, и каждой точке соответствует единственное число — ее координата. Это основа для визуализации числовых множеств и операций с ними.
Ключевые определения и принципы работы с координатной прямой можно найти в учебниках, включенных в Федеральный перечень. 1
Полезная информация о координатной прямой
Чтобы быстро ориентироваться в теме и всегда держать под рукой ключевые определения, сохраните эту таблицу-шпаргалку. В ней собраны основные элементы координатной прямой и их краткие объяснения. Это поможет вам моментально вспомнить нужную информацию при решении задач.
| Элемент координатной прямой | Описание |
|---|---|
| Начало отсчета | Точка, соответствующая числу 0. Является центром отсчета для всех остальных чисел |
| Единичный отрезок | Расстояние от 0 до 1. Задает масштаб прямой: все остальные расстояния измеряются в этих единицах |
| Положительное направление | Направление, в котором откладываются положительные числа. Обычно указывается стрелкой вправо |
| Координата точки | Число, соответствующее точке на прямой. Обозначается как A(x), где x — координата |
| Положительные числа | Располагаются справа от нуля (1; 3; 5,7; 2/5 и другие) |
| Отрицательные числа | Располагаются слева от нуля (-1; -5; -9,5; -3/4 и другие) |
Элементы координатной прямой
Чтобы уверенно работать с координатной прямой, нужно знать, из чего она состоит. Давайте разберем три ее главных элемента: точку отсчета, единичный отрезок и направление. Как только вы их поймете, любая задача с координатами станет простой и понятной.
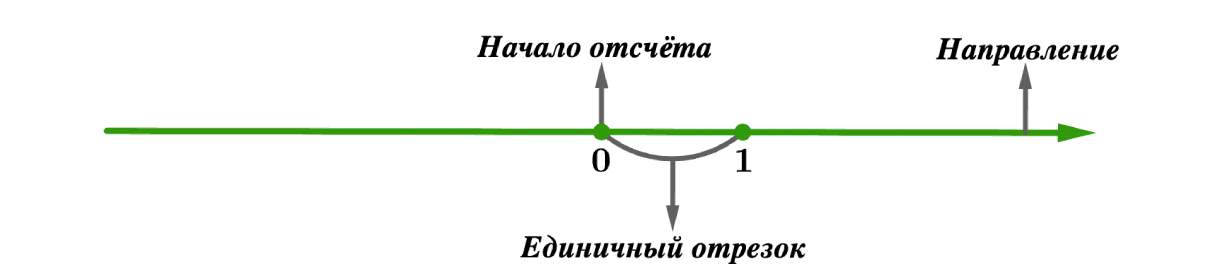
Начало отсчета
Началом отсчета является точка ноль (0), исходная точка для всех измерений. Она делит прямую на два луча: положительный (справа) и отрицательный (слева). Все расстояния до других точек отсчитываются именно от начала отсчета.
Единичный отрезок
Расстояние между точками 0 и 1 называется единичным отрезком. Именно оно задает масштаб всей координатной прямой. Его длину мы используем, чтобы отмерить координаты.
В учебных тетрадях единичный отрезок чаще всего равен одной клетке или двум, но в условии конкретной задачи может быть указана и другая его длина. Всегда обращайте внимание на чертеж и условие.
Положительное и отрицательное направления
Направление всегда задает то, как мы движемся по прямой.
- Положительное направление (чаще всего вправо): двигаясь в этом направлении, мы попадаем к точкам с бóльшими координатами.
- Отрицательное направление (противоположное, чаще всего влево): двигаясь в этом направлении, мы попадаем к точкам с мéньшими координатами.
Стрелка на конце прямой всегда указывает положительное направление.
Координаты точек на координатной прямой
Теперь, когда мы знаем элементы координатной прямой, научимся с ней работать с положительными и отрицательными числами. Есть две главные задачи: найти координату уже отмеченной точки и наоборот отметить точку с заданной координатой. Разберем каждую из них по шагам.
Как найти координату точки
Чтобы определить координату точки на координатной прямой:
- Найдите начало отсчета 0.
- Посмотрите, в какой стороне от нуля находится точка. Справа — координата положительна, слева — отрицательна.
- Измерьте расстояние от точки 0 до точки в единичных отрезках. Это число (со знаком «+» или «–») и будет координатой.
Пример
Если точка A находится справа от нуля на расстоянии трех единичных отрезков, ее координата A(3). Если точка B слева на расстоянии двух с половиной отрезков, ее координата B(-2,5).
Как отметить точку с заданной координатой
Чтобы отметить точку с заданной координатой на координатной прямой:
- Найдите начало отсчета 0.
- Определите направление движения. Если координата положительная, двигайтесь от нуля в положительном направлении (вправо). Если координата отрицательная, двигайтесь от нуля в отрицательном направлении (влево).
- Отложите расстояние. Для этого от точки 0 отсчитайте модуль числа единичных отрезков. Поставьте точку в конце отрезка и подпишите ее.
Пример
Чтобы отметить точку C(4), где координата положительная, от точки 0 нужно пройти вправо на 4 единичных отрезка. Чтобы отметить точку D(-3,7), где координата отрицательная, от точки 0 нужно пройти влево на 3,7 единичных отрезка.
Сравнение чисел на координатной прямой
Координатная прямая будет лучшим помощником для сравнения чисел. На ней наглядно работает простое правило, а именно: чем правее точка на координатной прямой, тем больше ее координата.
Из этого следуют все правила сравнения.
- Любое положительное число больше нуля и любого отрицательного числа.
- Любое отрицательное число меньше нуля и любого положительного числа.
- Из двух положительных чисел больше то, которое расположено правее (дальше от нуля).
- Из двух отрицательных чисел больше то, которое расположено правее (ближе к нулю).
Работа с координатной прямой является обязательным элементом школьного курса, что отражено в Федеральной рабочей программе по математике 2.
Задачи и ответы по теме «Координатная прямая»
Лучший способ закрепить теорию — применить ее на практике. Попробуйте решить эти задачи, чтобы проверить, как хорошо вы разобрались с координатной прямой. Под каждой задачей вы найдете подробное решение и ответ.
Задача 1
Отметьте точки A, B, C на координатной прямой, если известно, что точка A имеет координату 2, точка C координату -3, а координата точки B равна 0.
Решение и ответ к задаче 1
Находим начало отсчета, это точка B(0).
Чтобы отметить A(2), двигаемся от B(0) вправо на 2 единичных отрезка.
Чтобы отметить C(-3), двигаемся от B(0) влево на 3 единичных отрезка.
Ответ: точки отмечены на рисунке
Задача 2
Найдите координаты точек M и N, отмеченных на координатной прямой.
Решение и ответ к задаче 2
Точка M находится справа от нуля. Расстояние от 0 до M равно 5,5 единичным отрезкам. Значит, ее координата M(5,5).
Точка N находится слева от нуля. Расстояние от 0 до N равно 2 единичным отрезкам. Значит, ее координата N(-2).
Ответ: M(5,5), N(-2)
Задача 3
Сравните числа, используя правило сравнения на координатной прямой. Поставьте знак >, < или =.
а) -5 и 2
б) 0 и -1
в) -4 и -6
Решение и ответ к задаче 3
Вспоминаем правило: чем правее точка на прямой, тем больше ее координата.
а) -5 лежит левее 2 → -5 < 2
б) 0 лежит правее -1 → 0 > -1
в) -4 лежит правее -6 → -4 > -6
Ответ: а) -5 < 2; б) 0 > -1; в) -4 > -6
Задача 4
Между какими двумя соседними целыми числами на координатной прямой расположено число -2,7?
Решение и ответ к задаче 4
Число -2,7 — отрицательное. На координатной прямой оно лежит между ближайшими к нему целыми числами: -3 и -2. Проверим: -3 < -2,7 < -2.
Ответ: между целыми числа -3 и -2
Популярные вопросы и ответы
Отвечает Вероника Бороздина, старший преподаватель математики Домашней школы «ИнтернетУрок»:
Для чего нужна координатная прямая в математике?
Координатная прямая нужна для наглядного представления расположения действительных чисел. Также ее можно использовать для лучшего понимания сложения и вычитания чисел. Особенно, когда ученики изучают отрицательные числа. В более старших классах координатную прямую используют также для графического представления решений неравенств. И конечно, благодаря координатной прямой можно лучше понять определение модуля числа.
Сколько точек помещается на координатной прямой?
На координатной прямой нет ограничения по количеству точек, так как каждая точка соответствует определенному числу, а их бесконечное множество. Фактически координатная прямая ограничивается только размером ее изображения и как вы зададите единичный отрезок и сколько точек вы поставите.
Почему тему по математике «Координатная прямая» изучают в 5-6 классах?
Тему «Координатная прямая» изучают в 5-6 классах потому что она является базовым термином, на котором у детей строится представление о числах в целом, об операциях с числами. Она помогает научиться сравнивать числа и понять простейшие арифметические действия.
В каких заданиях ОГЭ и ЕГЭ по математике встречается координатная прямая?
Координатная прямая встречается во многих заданиях государственных экзаменов. В заданиях на решение неравенств, например №7 и №20 из ОГЭ, №18 из ЕГЭ (базовый уровень), №15 из ЕГЭ (профильный уровень). Причем задание №18 из базового уровня ЕГЭ бывает не только на решение неравенств, но и по теме «Числовые промежутки». Это такие задания, где нужно установить соответствие между указанными точками и числами.
Также координатная прямая может пригодиться в заданиях на решение уравнений для определения области допустимых значений. Это задания №20 из ОГЭ, №17 из ЕГЭ (базовый уровень), №6 и №13 из ЕГЭ (профильный уровень). И в других заданиях: в заданиях на поиск наибольшего и наименьшего значения функции, в заданиях с графиками функций, где уже не просто координатная прямая, а координатная плоскость, и так далее.
Для отработки подобных заданий рекомендуется использовать Открытый банк заданий ФИПИ,3 где собраны официальные прототипы задач с экзаменов.
Также координатная прямая может пригодиться в заданиях на решение уравнений для определения области допустимых значений. Это задания №20 из ОГЭ, №17 из ЕГЭ (базовый уровень), №6 и №13 из ЕГЭ (профильный уровень). И в других заданиях: в заданиях на поиск наибольшего и наименьшего значения функции, в заданиях с графиками функций, где уже не просто координатная прямая, а координатная плоскость, и так далее.
Для отработки подобных заданий рекомендуется использовать Открытый банк заданий ФИПИ,3 где собраны официальные прототипы задач с экзаменов.
Источники
Материал подготовлен на основании официальных документов и рекомендаций:
- Министерство просвещения России. Федеральный перечень учебников. URL: https://fpu.edu.ru/
Виленкин Н.Я., Жохов В.И., Чесноков А.С. и другие. «Математика. 5 класс. Базовый уровень»
Виленкин Н.Я., Жохов В.И., Чесноков А.С. и другие. «Математика. 6 класс. Базовый уровень»
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и другие. «Алгебра. 7 класс. Базовый уровень.»
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и другие. «Алгебра. 8 класс. Базовый уровень.» - Министерство просвещения России. Федеральная рабочая программа по учебному предмету «Математика». URL: https://static.edsoo.ru/projects/fop/index.html#/sections/200215
- Федеральный институт педагогических измерений. Открытый банк заданий ОГЭ и ЕГЭ по математике. Методические рекомендации для учителей. URL: https://fipi.ru/
