Линейная функция
Узнаем, что такое линейная функция, научимся строить ее график, понимать смысл ее коэффициентов и анализировать свойства, а также разберемся, как по формуле определить взаимное расположение прямых на плоскости
Представьте, что вы открываете приложение такси. Стоимость поездки складывается из фиксированного тарифа, например 100 рублей за подачу машины, и суммы, которая растет пропорционально расстоянию, например +30 рублей за каждый километр. Итоговая цена зависит от длины маршрута по простому правилу: чем дальше едешь, тем больше платишь. Эта и множество других повседневных зависимостей устроены по единому математическому закону, они описываются линейной функцией.
В этой статье вместе с преподавателем математики и программирования Артемом Островским мы разберем, как устроена линейная функция, научимся строить ее график — прямую линию, и поймем, как два числа в формуле, угловой коэффициент и свободный член, влияют на наклон и положение этой прямой на координатной плоскости.
Что такое линейная функция в алгебре
Согласно определению из учебника Л. С. Атанасяна «Геометрия. 7–9 классы», входящем в Федеральный перечень учебников:1 функция, или функциональная зависимость, — это зависимость одной переменной от другой, где каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Независимую переменную иначе называют аргументом, о зависимой переменной говорят, что она является функцией от этого аргумента, а ее значения называют значениями функции.
Линейная функция — это функция вида y = kx + b, где:
- x — независимая переменная (аргумент),
- y — зависимая переменная (функция),
- k и b — действительные числа, называемые коэффициентами.
Главная особенность линейной функции: ее график всегда является прямой линией. Число k называют угловым коэффициентом, он определяет наклон прямой относительно оси абсцисс (OX), а b — свободным членом, указывающим точку пересечения графика с осью ординат (OY).
Полезная информация о линейной функции
Чтобы быстро ориентироваться в ключевых аспектах линейной функции и всегда держать под рукой главные факты, сохраните эту таблицу-шпаргалку.
| Линейная функция | Описание |
|---|---|
| Общий вид | y = kx + b |
| Переменные | x — независимая переменная (аргумент)y — зависимая переменная (функция) |
| Угловой коэффициент (k) | Определяет угол наклона прямой:k > 0 — функция возрастаетk < 0 — функция убываетk = 0 — прямая параллельна оси OX |
| Свободный член (b) | Ордината точки пересечения с осью OY: (0; b) |
| График | Прямая |
График линейной функции
Графиком линейной функции y = kx + b является прямая.
Из геометрии мы помним важную аксиому: через любые две точки можно провести прямую, и притом только одну. Это свойство лежит в основе построения графика. Чтобы изобразить его, достаточно найти координаты двух любых точек, удовлетворяющих уравнению, и провести через них прямую линию.
Важное следствие: линейная функция полностью определяется своими коэффициентами k и b. Зная их, мы можем предсказать поведение графика, не строя его детально.
это интересно
Пошаговая инструкция по построению графика линейной функции
Следуйте этому алгоритму, чтобы безошибочно строить прямые для любой линейной функции.
1. Запишите формулу функции. Убедитесь, что она приведена к виду y = kx + b.
2. Найдите координаты двух точек.
Выберите два любых, удобных для расчетов значения аргумента x1 и x2. Подставьте их поочередно в формулу y = kx + b, чтобы вычислить соответствующие значения y1 и y2. Вы получите две точки с координатами (x1; y1) и (x2; y2).
Лайфхак
Часто самыми удобными на практике точками являются точки пересечения графика с осями координат. Чтобы найти точку пересечения с осью ординат (OY), подставьте x = 0 — получите точку (0; b). Пересечение с осью абсцисс (OX) происходит при y = 0. Решив уравнение kx + b = 0 относительно x, получим точку (-b/k; 0) при k ≠ 0.
3. Отметьте найденные точки на координатной плоскости.
4. Проведите через эти точки прямую, используя линейку. Продолжите прямую за отмеченные точки в обе стороны, чтобы подчеркнуть, что график функции — бесконечная прямая, а не отрезок.
5. Подпишите график его уравнением.
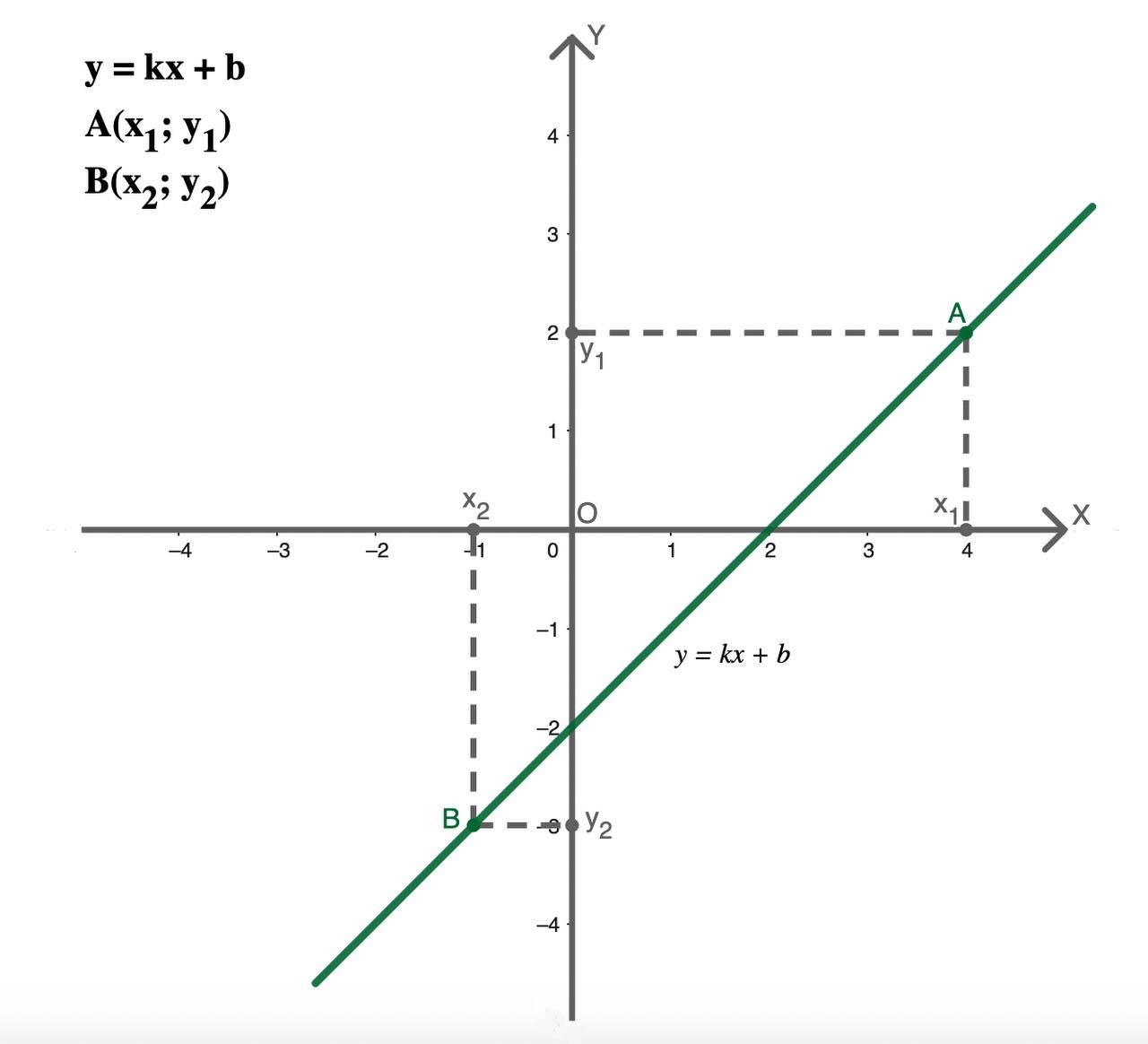
Примеры построения графика линейной функции
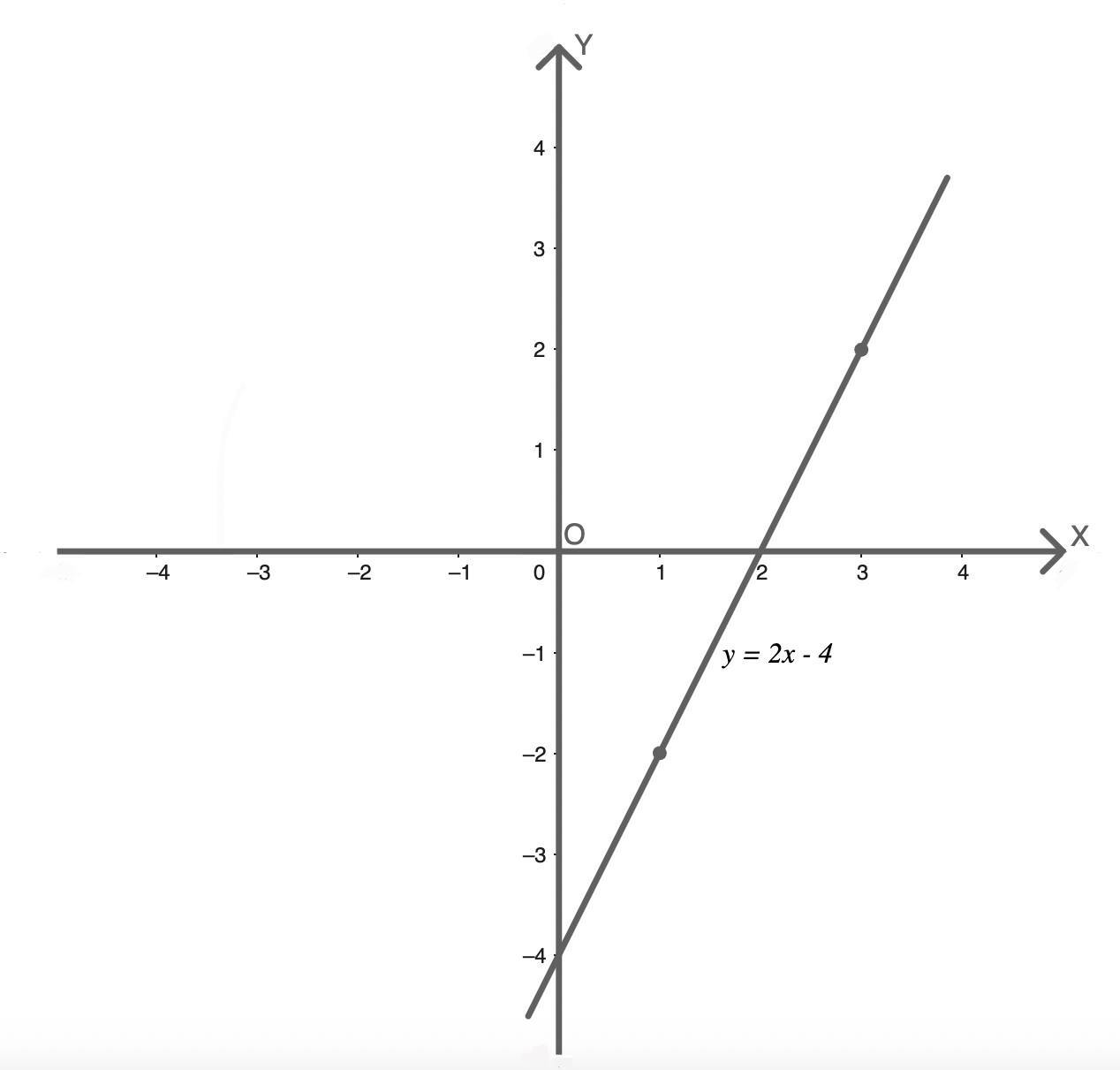
Построим график функции: y = 2x — 4.
1. Находим координаты двух выбранных точек:
При x = 1: y = 2 × 1 — 4 = -2 → A(1; -2).
При x = 3: y = 2 × 3 — 4 = 2 → B(3; 2).
2. Отмечаем точки A и B на координатной плоскости.
3. Проводим прямую через точки A и B и подписываем график.
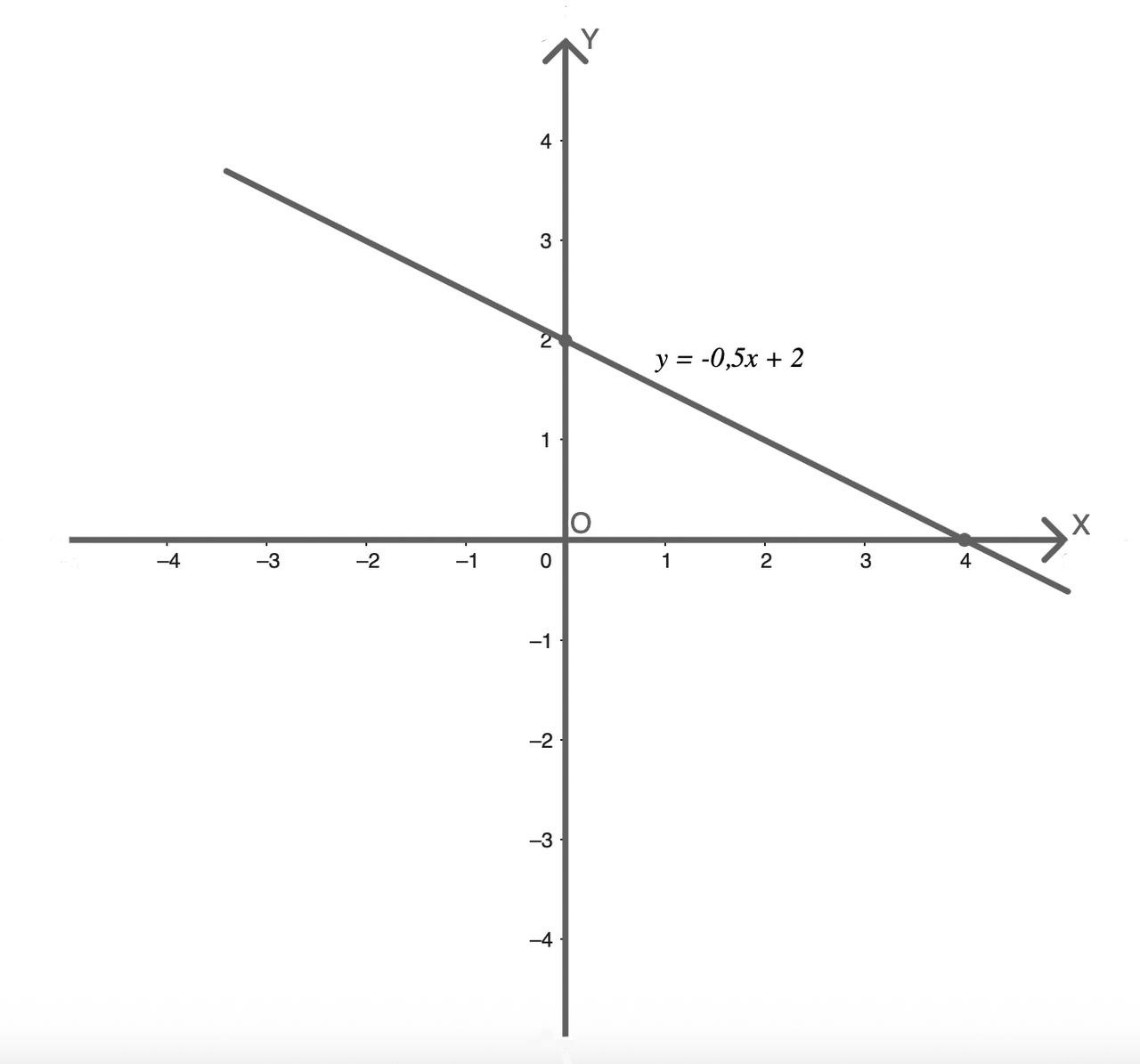
Построим график функции: y = -0,5x + 2.
1. Находим координаты точек пересечения с осями:
При x = 0: y = -0,5 × 0 + 2 = 2 → A(0; 2).
При y = 0: -0,5x + 2 = 0 → x = 4 → B(4; 0).
2. Отмечаем точки A и B на координатной плоскости.
3. Проводим прямую через точки A и B и подписываем график.
Коэффициенты линейной функции
Мы уже выяснили, что линейная функция описывается формулой y = kx + b. Теперь разберемся, за что отвечают коэффициенты k и b. Их главная сила в том, что, просто зная их значения, мы можем предсказать, как будет выглядеть график: куда наклонена прямая и где она пересекает ось OY. И наоборот, взглянув на график, можно с уверенностью сказать, каковы знаки коэффициентов и даже приблизительно оценить их значения.
Угловой коэффициент линейной функции
Угловой коэффициент k определяет наклон прямой относительно оси абсцисс (OX) и, следовательно, характер ее изменения, а именно возрастает функция или убывает.
Если k > 0, угол наклона между прямой и положительным направлением оси OX острый. Прямая наклонена вправо вверх, поднимается при движении слева направо. Чем больше k, тем круче подъем. Функция возрастает.
Если k < 0, угол наклона между прямой и положительным направлением оси OX тупой. Прямая наклонена вправо вниз, опускается при движении слева направо. Чем меньше k (больше по модулю с отрицательным знаком), тем круче спуск. Функция убывает.
Если k = 0, прямая параллельна оси OX. Это случай постоянной функции y = b, которая не возрастает и не убывает.
В старших классах, когда вы начнете изучать тригонометрию, откроется важный геометрический факт. Оказывается, угловой коэффициент k численно равен тангенсу угла α, который данная прямая образует с положительным направлением оси абсцисс OX. То есть справедлива формула k = tg α. Это объясняет, почему при k > 0 угол острый (tg α > 0), а при k < 0 угол тупой (tg α < 0). Таким образом, зная уравнение прямой, вы сможете вычислить точный угол ее наклона, и наоборот.
Свободный член линейной функции
Свободный член b показывает, где прямая встречается с осью ординат (OY). Координата точки пересечения с осью OY всегда равна (0; b). Знак b определяет, выше или ниже начала координат пройдет прямая: b > 0 — пересечение выше нуля, b < 0 — ниже.
Зависимость графика линейной функции от коэффициентов
Давайте наглядно посмотрим, как сочетание знаков коэффициентов k и b определяет положение прямой на координатной плоскости. На одной схеме можно увидеть все ключевые случаи.
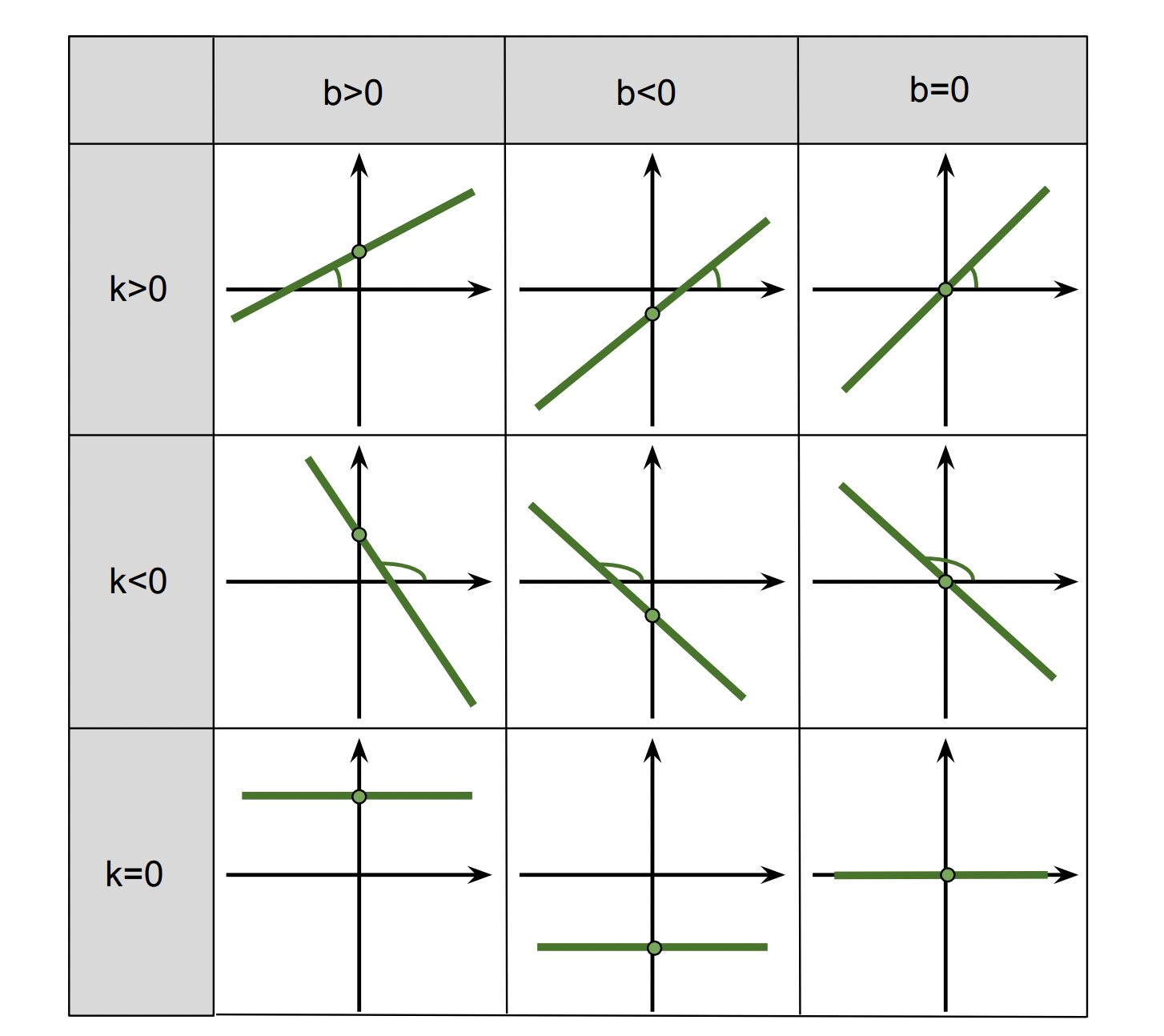
Свойства линейной функции
Любая функция характеризуется набором свойств: где она определена, как меняется, какие особые точки имеет. Зная формулу линейной функции, мы можем сразу, даже без построения графика, описать все ее ключевые особенности. Разберем их по порядку.
Область определения и область значений
Область определения: D(y) = R (все действительные числа). Аргумент x может принимать любое значение.
Область значений: E(y) = R (все действительные числа), если k ≠ 0. Если k = 0, то функция имеет вид y = b (константа), и ее область значений состоит из одного числа b.
Монотонность
Если k > 0, функция возрастает на всей числовой прямой: большему значению x соответствует большее значение y.
Если k < 0, функция убывает на всей числовой прямой: большему значению x соответствует меньшее значение y.
Если k = 0, функция постоянна на всей числовой прямой (y = b).
Нули функции
Нуль функции — это значение аргумента x, при котором значение функции y равно нулю. Для его нахождения решают уравнение kx + b = 0.
При k ≠ 0 существует ровно один нуль функции: x = -b/k. График пересекает ось OX в точке (-b/k; 0).
При k = 0 и b ≠ 0 нулей функции нет (горизонтальная прямая не пересекает ось OX).
При k = 0 и b = 0 функция тождественно равна нулю (y = 0), и любое x является нулем функции.
Наибольшее и наименьшее значение
На всей области определения линейная функция, где k ≠ 0, не имеет ни наибольшего, ни наименьшего значения, так как ее значения неограниченно растут или убывают в зависимости от монотонности.
Если k = 0 (функция y = b), то ее наибольшее и наименьшее значение равны b.
Четность и нечетность
Функция называется четной, если f(-x) = f(x), то есть график симметричен относительно оси OY.
Функция называется нечетной, если f(-x) = -f(x), то есть график симметричен относительно начала координат.
Линейная функция y = kx + b является нечетной только в случае, когда b = 0, то есть y = kx. Во всех остальных случаях функция не является ни четной, ни нечетной.
Взаимное расположение графиков линейных функций
Мы уже разобрались, что такое линейная функция, научились строить ее график и изучили свойства. Но что, если на одной координатной плоскости построить несколько графиков линейных функций? Они могут быть параллельны, пересекаться под разными углами или даже совпадать. Чтобы определить их взаимное расположение, не обязательно строить графики, достаточно сравнить коэффициенты k и b в их уравнениях.
Параллельные прямые
Две прямые, заданные уравнениями y = k1x + b1 и y = k2x + b2, параллельны тогда и только тогда, когда их угловые коэффициенты равны, а свободные члены различны:
k1 = k2 и b1 ≠ b2
Пример
Прямые y = 3x — 1 и y = 3x + 5 параллельны, так как k1 = k2 = 3, но b1 ≠ b2.
Совпадающие прямые
Частный (предельный) случай параллельности, когда прямые не просто параллельны, а полностью совпадают. Это происходит, когда равны и угловые коэффициенты, и свободные члены:
k1 = k2 и b1 = b2
В этом случае оба уравнения описывают одну и ту же прямую.
Пересекающиеся прямые
Две прямые, заданные уравнениями y = k1x + b1 и y = k2x + b2, пересекаются, если их угловые коэффициенты различны:
k1 ≠ k2
Чтобы найти координаты единственной точки пересечения, нужно приравнять правые части уравнений и решить полученное уравнение относительно x:
k1x + b1 = k2x + b2
Найденная абсцисса x подставляется в любое из исходных уравнений для вычисления ординаты y.
Пример
Прямые y = 4x — 3 и y = x + 6 пересекаются, так как k1 = 4, а k2 = 1. Найдем точку пересечения. Приравниваем 4x — 3 = x + 6 →3x = 9 → x = 3. Подставляем x = 3 в первое уравнение: y = 4 × 3 — 3 = 9. Точка пересечения (3; 9).
Перпендикулярные прямые
Две прямые, заданные уравнениями y = k1x + b1 и y = k2x + b2, перпендикулярны, если произведение их угловых коэффициентов равно -1:
k1 × k2 = -1
Пример
Прямые y = 2x + 1 и y = -0.5x + 4 перпендикулярны, так как k1 × k2 = 2 × (-0.5) = -1.
Задачи и ответы по теме «Линейная функция»
Решим несколько задач по изученной теме.
Задача 1
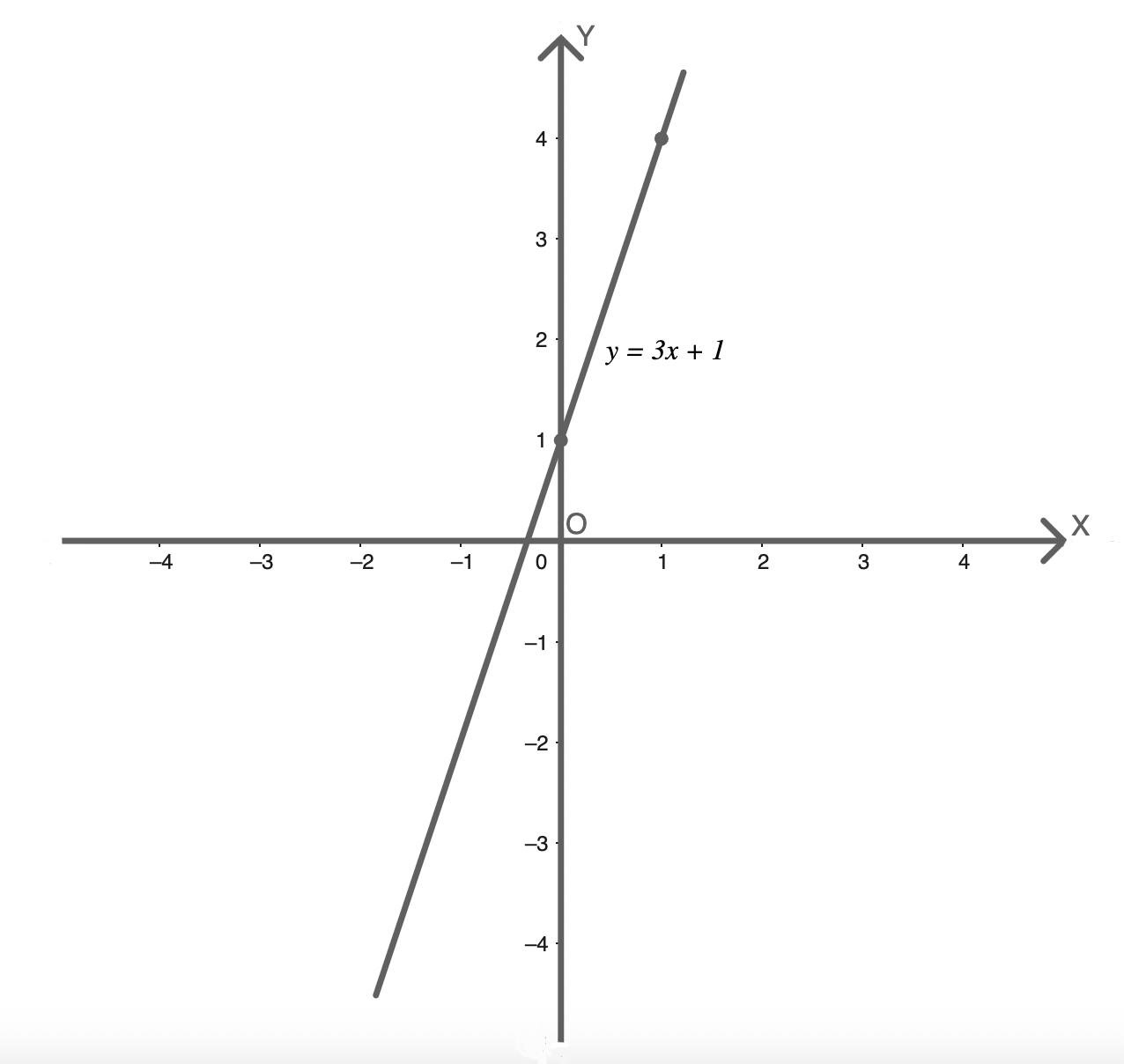
Постройте график функции y = 3x + 1.
Решение и ответ к задаче 1
Находим координаты двух выбранных точек:
При x = 0: y = 3 × 0 + 1 = 1 → A(0; 1).
При x = 1: y = 3 × 1 + 1 = 4 → B(1; 4).
Отмечаем точки A и B на координатной плоскости и проводим прямую через точки A и B.
Задача 2
Найдите координаты точек пересечения графика функции y = −x + 4 с осями координат, не строя его.
Решение и ответ к задаче 2
Точкe пересечения с осью OX находим при y = 0:
-x + 4 = 0, x = 4 → (4; 0)
Точку пересечения с осью OY находим при x = 0:
y = -0 + 4 = 4 → (0; 4)
Ответ: (4; 0); (0; 4)
Задача 3
Найдите нуль функции y = 0,5x — 2.
Решение и ответ к задаче 3
Нуль функции находим при y = 0:
0,5x — 2 = 0
0,5x = 2
x = 4
Ответ: 4
Задача 4
Известно, что график линейной функции y = kx + 3 проходит через точку A(−1;5). Найдите коэффициент k и запишите уравнение функции. Какое значение принимает функция при x = 1? При каком значении x функция принимает значение −7?
Решение и ответ к задаче 4
Так как график заданной функции проходит через точку A(−1;5), то при подстановке координат точки в формулу должно выполняться верное равенство:
k × (-1) + 3 = 5
Решим полученное уравнение относительно k:
-k + 3 = 5
-k = 2
k = -2
Получим уравнение функции:
y = -2x + 3
Найдем значение функции при x = 1:
y = -2 × 1 + 3 = 1
Найдем x, при котором значение функции y = -7:
-2x + 3 = -7
-2x = -10
x = 5
Ответ: k = -2; y = -2x + 3; y = 1; x = 5
Задача 5
Определите взаимное расположение прямых, заданных уравнениями, не строя их графики:
а) y = 5x − 2 и y = 5x + 4;
б) y = ⅔x + 1 и y = −1,5x − 2.
Решение и ответ к задаче 5
а) Для функции y = 5x — 2 определяем коэффициенты:
k1 = 5, b1 = -2
Для функции y = 5x + 4 определяем коэффициенты:
k2 = 5, b2 = 4
Так как k1 = k2 и b1 ≠ b2, прямые параллельны.
б) Для функции y = ⅔x + 1 определяем коэффициенты:
k1 = ⅔, b1 = 1
Для функции y = −1,5x − 2 определяем коэффициенты:
k2 = -1,5, b2 = -2
Произведение коэффициентов k1 × k2 = ⅔ × (-1,5) = -1, значит, прямые перпендикулярны.
Ответ: а) прямые параллельны; б) прямые перпендикулярны
Популярные вопросы и ответы
Отвечает Артем Островский, преподаватель курсов программирования и машинного обучения Московского физико-технического института, куратор заочной физико-технический школы МФТИ по физике и математике:
Как найти точку пересечения графиков двух линейных функций, не строя их?
Чтобы найти точку пересечения, можно, конечно, построить оба графика и визуально определить координаты. Однако быстрее и, что важнее, гораздо точнее поможет простой аналитический метод. Он основан на ключевом свойстве: искомая точка лежит на обеих прямых одновременно, а значит, ее координаты (x; y) должны удовлетворять уравнениям обеих функций. Это значит, что значения y, рассчитанные по каждой из формул для одного и того же x, обязаны быть равны.
Для этого нужно приравнять правые части формул k1x + b1 и k2x + b2. Получившееся уравнение k1x + b1 = k2x + b2 решается относительно x — это и будет абсцисса точки. Затем найденный x подставляется в любую из исходных формул, чтобы получить ординату y.
Например, для функций y = 2x + 1 и y = -x + 7 получим уравнение 2x + 1 = -x + 7. Решив его, находим x = 2, а затем y = 5. Ответ: точка пересечения (2; 5). Кстати, если в процессе решения получается неверное равенство (например, 5 = 0), значит, прямые параллельны и не пересекаются.
Для этого нужно приравнять правые части формул k1x + b1 и k2x + b2. Получившееся уравнение k1x + b1 = k2x + b2 решается относительно x — это и будет абсцисса точки. Затем найденный x подставляется в любую из исходных формул, чтобы получить ординату y.
Например, для функций y = 2x + 1 и y = -x + 7 получим уравнение 2x + 1 = -x + 7. Решив его, находим x = 2, а затем y = 5. Ответ: точка пересечения (2; 5). Кстати, если в процессе решения получается неверное равенство (например, 5 = 0), значит, прямые параллельны и не пересекаются.
Почему тему по алгебре «Линейная функция» изучают в 7 классе?
Тема «Линейная функция» — это не случайный выбор, а продуманная основа, на которую будет опираться вся дальнейшая школьная алгебра. К 7 классу ученики уже уверенно работают с числами, переменными и простейшими уравнениями. Линейная функция становится первой моделью, где они видят закон, связывающий две переменные, и его графическое представление.
Это отличная тема, чтобы на понятном примере ввести ключевые абстрактные понятия: что такое функция, аргумент, коэффициент, область определения, график. Прямая линия является самым наглядным графиком. Работая с ней, дети в комфортном режиме осваивают навык перехода от формулы к графику и обратно, учатся анализировать зависимость по коэффициентам. Без этого уверенного старта невозможно двигаться дальше к квадратичным, показательным или тригонометрическим функциям, которые будут казаться слишком сложными.
Таким образом, это отличная тема, чтобы на понятном примере ввести ключевые абстрактные понятия, обязательные к освоению согласно Федеральной рабочей программе по математике.2
Это отличная тема, чтобы на понятном примере ввести ключевые абстрактные понятия: что такое функция, аргумент, коэффициент, область определения, график. Прямая линия является самым наглядным графиком. Работая с ней, дети в комфортном режиме осваивают навык перехода от формулы к графику и обратно, учатся анализировать зависимость по коэффициентам. Без этого уверенного старта невозможно двигаться дальше к квадратичным, показательным или тригонометрическим функциям, которые будут казаться слишком сложными.
Таким образом, это отличная тема, чтобы на понятном примере ввести ключевые абстрактные понятия, обязательные к освоению согласно Федеральной рабочей программе по математике.2
В каких заданиях ОГЭ и ЕГЭ встречаются задачи на линейную функцию?
Тема «Линейная функция» важна как на ОГЭ в 9 классе, так и на ЕГЭ в 11 классе, но проявляется она на этих экзаменах по-разному. На ОГЭ линейная функция часто выступает прямым объектом заданий, например, в задачах на чтение графиков, где требуется определять знаки коэффициентов, сопоставлять формулы с соответствующими графиками, а также может встретиться в задаче повышенного уровня во второй части, где требуется построить самостоятельно график функции или выполнить более глубокий анализ.
На ЕГЭ профильного уровня линейная зависимость становится частью более сложных конструкций. Она используется в экономических моделях, в задачах с параметром, где нужно анализировать взаимное расположение прямых, и в теме производной, поскольку уравнение касательной — это тоже линейная функция. Для эффективной подготовки к такого рода заданиям настоятельно рекомендуется обращаться к заданиям из Открытого банка ФИПИ3, где можно найти актуальные прототипы экзаменационных задач.
На ЕГЭ профильного уровня линейная зависимость становится частью более сложных конструкций. Она используется в экономических моделях, в задачах с параметром, где нужно анализировать взаимное расположение прямых, и в теме производной, поскольку уравнение касательной — это тоже линейная функция. Для эффективной подготовки к такого рода заданиям настоятельно рекомендуется обращаться к заданиям из Открытого банка ФИПИ3, где можно найти актуальные прототипы экзаменационных задач.
Источники
Материал подготовлен на основании официальных документов и рекомендаций:
1. Министерство просвещения России. Федеральный перечень учебников. URL: https://fpu.edu.ru/
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. «Геометрия. 7-9 классы. Базовый уровень»
- Смирнов В.А., Смирнова И.М. «Геометрия. 7 класс»
- Смирнов В.А., Смирнова И.М. «Геометрия. 8 класс»
- Смирнов В.А., Смирнова И.М. «Геометрия. 9 класс»
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. «Геометрия. 10-11 классы. Базовый и углубленный уровни»
- Мерзляк А.Г., Номировский Д.А., Поляков В.М. «Геометрия. 10 класс. Углубленный уровень»
- Мерзляк А.Г., Номировский Д.А., Поляков В.М. «Геометрия. 11 класс. Углубленный уровень»
2. Министерство просвещения России. Федеральная рабочая программа по учебному предмету «Математика». URL: https://static.edsoo.ru/projects/fop/index.html#/sections/200215
3. Федеральный институт педагогических измерений. Открытый банк заданий ОГЭ и ЕГЭ по математике. Методические рекомендации для учителей. URL: https://fipi.ru/
