Описанная окружность
Разберемся, что такое описанная окружность, около каких фигур ее можно построить и как ее свойства помогают находить углы, стороны и площади вписанных многоугольников
Мы знакомы с различными многоугольниками в геометрии. Некоторые из них позволяют разместить окружность так, чтобы она проходила через все их вершины. Такая окружность не просто описана вокруг фигуры, она находится с ней в строгом геометрическом соответствии, где положение ее центра и величина радиуса подчиняются конкретным законам. И называется такая окружность описанной.
Вместе с преподавателем математики Артемом Островским разберемся что такое описанная окружность, около каких фигур ее можно описать, какими свойствами она обладает и чем она отличается от вписанной окружности.
Что такое описанная окружность в геометрии
Согласно определению из учебника Л. С. Атанасяна «Геометрия. 7–9 классы», входящем в Федеральный перечень учебников:1 описанная окружность — это окружность, которая проходит через все вершины многоугольника. Сам многоугольник в таком случае называется вписанным в окружность.
Центр описанной окружности равноудален от всех вершин многоугольника. Это прямо следует из определения окружности как множества точек, равноудаленных от центра.
Возможность описать окружность является особым свойством фигуры. Например, это всегда возможно для любого треугольника, но для четырехугольника и других многоугольников необходимо соблюдение строгих условий. Подробно разберем каждый случай ниже.
Полезная информация об описанной окружности
Чтобы уверенно работать с описанной окружностью, важно помнить ее основные элементы и отличия. Эта таблица поможет быстро освежить в памяти ключевые факты.
| Описанная окружность | Описание |
|---|---|
| Центр | Точка, равноудаленная от всех вершин вписанного многоугольника |
| Радиус (R) | Расстояние от центра до любой вершины многоугольника |
| Основное свойство | Окружность проходит через все вершины фигуры |
| Отличие от вписанной окружности | Вписанная окружность касается всех сторон, а описанная проходит через все вершины |
Описанная окружность около треугольника
Вокруг любого треугольника можно описать окружность, и притом только одну. Центр этой окружности является одной из замечательных точек треугольника, называемый центром описанной окружности, или циркумцентром.
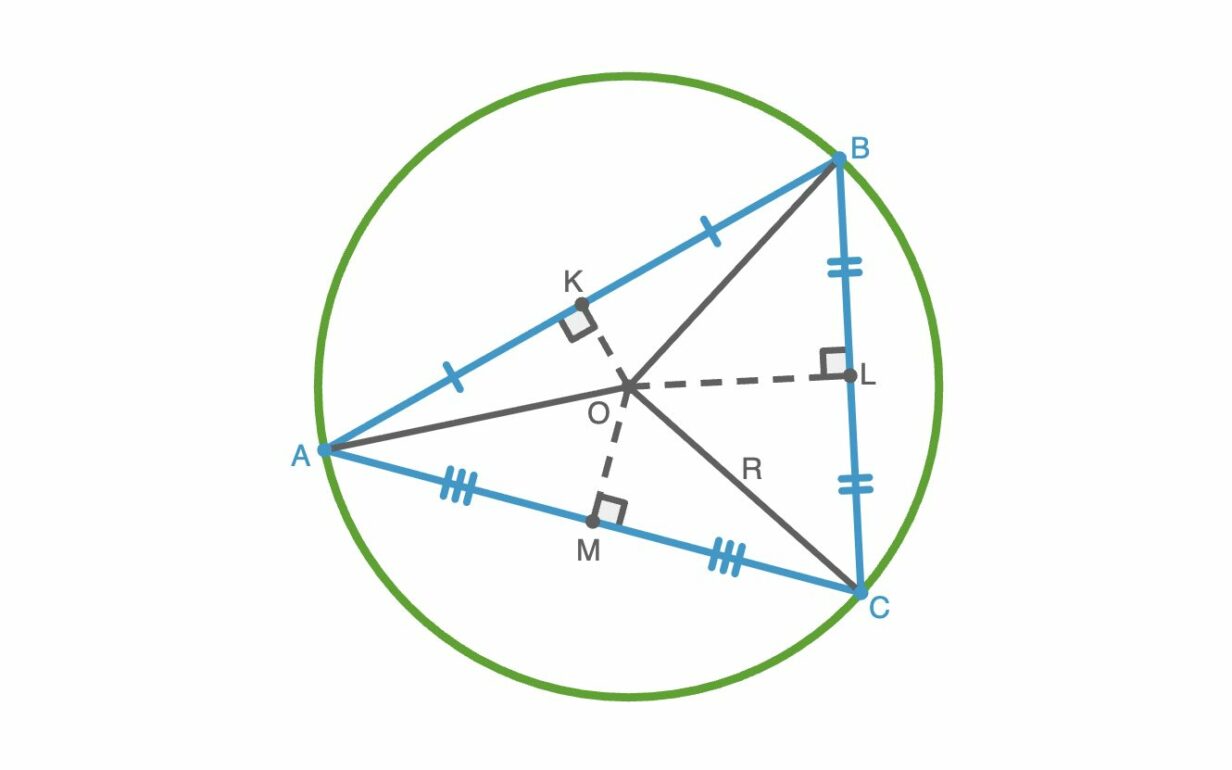
Свойства описанной окружности около треугольника
Описанная около треугольника окружность подчиняется закономерностям, которые связывают ее центр и радиус со сторонами и углами фигуры. Эти свойства, в свою очередь, лежат в основе других важных теорем и полезных формул.
1. Центр лежит на пересечении серединных перпендикуляров к сторонам. Это главное свойство, позволяющее построить описанную окружность.
2. Центр окружности по-разному расположен относительно треугольника: в остроугольном — внутри, в прямоугольном — на середине гипотенузы, в тупоугольном — вне треугольника.
3. Площадь вписанного треугольника равна произведению длин его сторон, деленное на четыре радиуса описанной окружности:
4. Радиус описанной окружности около треугольника можно найти, поделив произведение длин сторон треугольника на четыре площади треугольника.
Это прямое следствие из предыдущего свойства. Площадь треугольника при этом можно найти различными способами, используя длину сторон треугольника, высоты, радиус вписанной окружности и другие.
5. Радиус описанной окружности около равностороннего треугольника можно найти по формуле:
6. Радиус описанной окружности около прямоугольного треугольника можно найти по формуле:
Медиана, проведенная к гипотенузе, равна ее половине и совпадает с радиусом описанной окружности.
7. Теорема синусов является ключевым следствием описанной окружности. Из нее можно выразить равенства, помогающие найти сторону треугольника или радиус окружности:
Описанная окружность около четырехугольника
Не около каждого четырехугольника можно описать окружность. Для этого необходимо и достаточно выполнение особого условия, которое называют признаком вписанного четырехугольника: сумма противоположных углов четырехугольника должна быть равна 180 градусам.
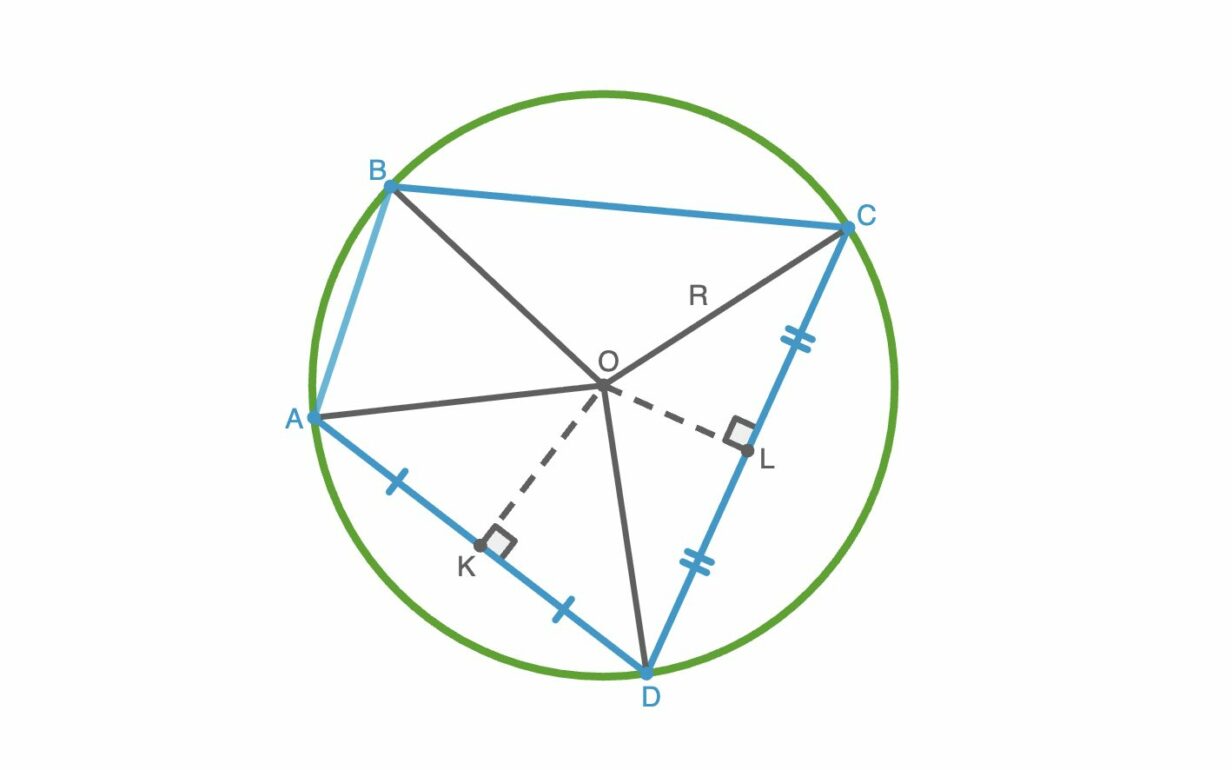
Свойства описанной окружности около четырехугольника
Описанная окружность накладывает на четырехугольник строгие ограничения, которые порождают несколько важных свойств и соотношений.
1. У описанного около окружности четырехугольника суммы противоположных углов равны 180°. Это основное и необходимое условие, позволяющее определить, можно ли описать окружность.
2. Окружность всегда можно описать около прямоугольника, квадрата и равнобедренной трапеции. Это следствие вытекает из предыдущего свойства.
3. Центр описанной окружности лежит на пересечении серединных перпендикуляров к любым двум сторонам четырехугольника.
4. Для вписанного четырехугольника верна теорема Птолемея: произведение длин его диагоналей равно сумме произведений длин противоположных сторон.
5. Диагонали вписанного четырехугольника разбивают его на четыре треугольника, которые образуют две пары подобных друг другу треугольников.
6. Если вписанный четырехугольник является квадратом, то радиус описанной окружности равен половине его диагонали:
7. Величина внешнего угла вписанного четырехугольника равна величине внутреннего угла, не смежного с ним. Это прямое следствие из основного свойства.
это интересно
Описанная окружность около многоугольника
Описать окружность можно не около любого многоугольника. Однако около любого правильного многоугольника окружность описать можно всегда. Для произвольного неправильного многоугольника с количеством сторон больше четырех это возможно только при соблюдении специальных условий. В школьном курсе и на экзаменах подробно изучается только случай правильных многоугольников, поэтому далее мы сосредоточимся именно на них.
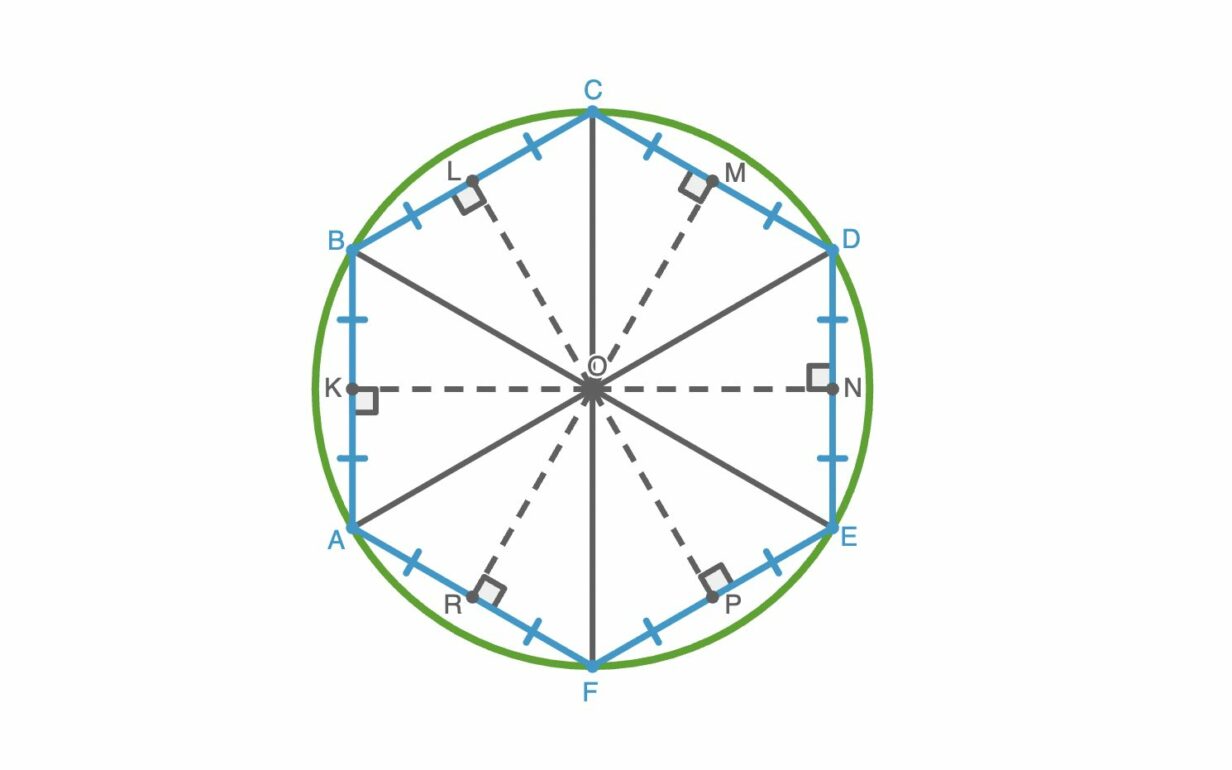
Свойства описанной окружности около правильного n-угольника
Рассмотрим все основные свойства описанной около правильного многоугольника окружности. В данном случае свойства проявляются в наиболее полной и симметричной форме.
1. Центр описанной окружности совпадает с центром правильного многоугольника. Это точка, равноудаленная от всех вершин.
2. Радиус описанной окружности, проведенный в вершину правильного многоугольника, является биссектрисой его внутреннего угла.
3. Площадь правильного многоугольника, вписанного в описанную окружность, можно найти по формуле, связывающей ее с радиусом и числом сторон:
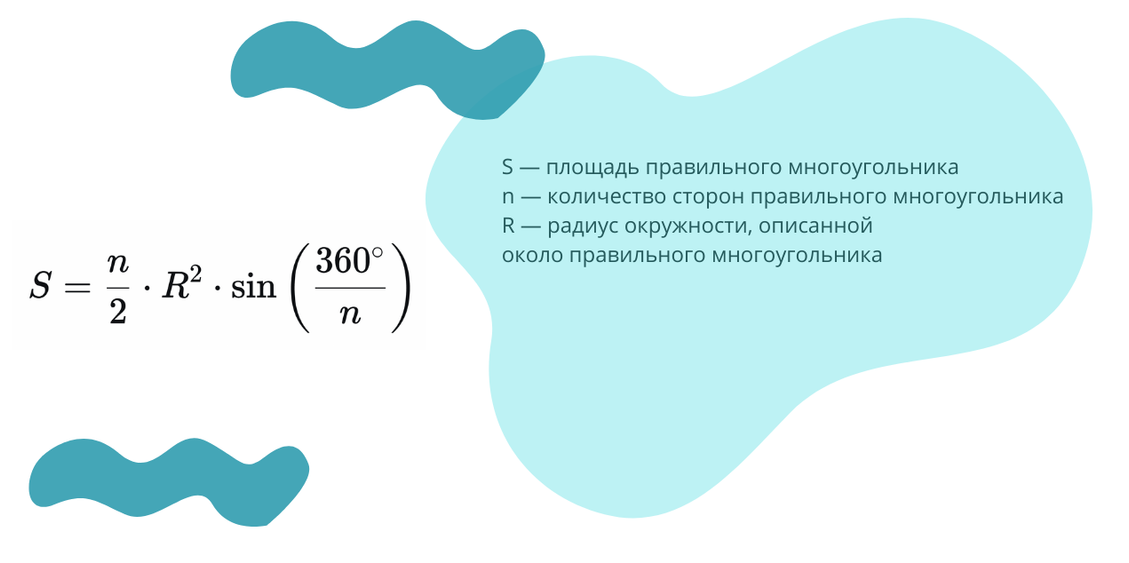
4. Радиус окружности, описанной около правильного многоугольника, можно найти через его сторону и число сторон:
Две последние формулы легко выводятся при рассмотрении равнобедренного треугольника, образованного двумя радиусами R, проведенными в соседние вершины, и стороной a многоугольника. Центральный угол этого треугольника равен 360°/n. Если провести высоту в этом треугольнике к основанию, то образуется прямоугольный треугольник с углом 180°/n. Из него и получается связь между радиусом, стороной и углом 180°/n.
Описанная окружность в архитектуре и искусстве
Правильные многоугольники, вписанные в окружность, издревле служили основой для создания гармоничных пропорций в архитектуре и искусстве. Знаменитый римский Пантеон, увенчанный совершенным полусферическим куполом, в своей основе имеет цилиндр, который можно представить как правильный многоугольник с очень большим числом сторон, вписанный в окружность. Эта геометрическая чистота рождает ощущение космического порядка и равновесия.
В эпоху Возрождения Леонардо да Винчи в своем знаменитом рисунке «Витрувианский человек» буквально вписал фигуру человека в круг и квадрат, исследуя идеальные пропорции. Круг (описанная окружность) здесь символизирует божественное, космическое начало и совершенство формы, к которому стремились архитекторы и художники, используя точные геометрические построения.
Задачи и ответы по теме «Описанная окружность»
Проверим, как хорошо вы усвоили теорию. Решение задач является лучшим способом закрепить формулы и научиться видеть, какое свойство описанной окружности нужно применить в конкретной ситуации. Начнем с простых упражнений и постепенно перейдем к более сложным.
Задача 1
Гипотенуза прямоугольного треугольника равна 26 см. Найдите радиус окружности, описанной около этого треугольника.
Решение и ответ к задаче 1
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, следовательно, радиус равен ее половине:
R = c / 2
R = 26 / 2 = 13 (см)
Ответ: 13 см
Задача 2
Один из углов вписанного в окружность четырехугольника равен 83°. Найдите величину противоположного ему угла.
Решение и ответ к задаче 2
По основному свойству вписанного в окружность четырехугольника, сумма противоположных углов равна 180°, следовательно, искомый угол равен:
180° — 83° = 97°
Ответ: 97°
Задача 3
Стороны треугольника равны 4 см, 13 см и 15 см. Найдите радиус окружности, описанной около этого треугольника.
Решение и ответ к задаче 3
Найдем площадь треугольника по формуле Герона:
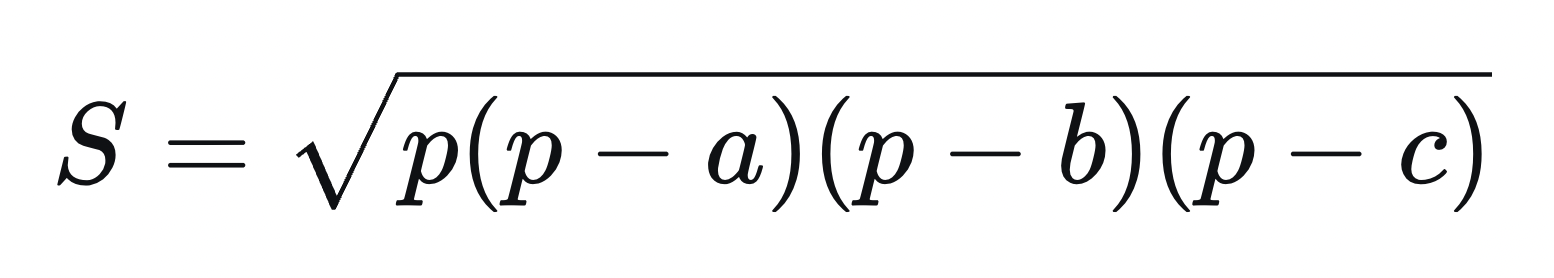
Для этого найдем полупериметр треугольника:
p = P / 2 = (a + b + c) / 2
p = (4 + 13 + 15) / 2 = 16 (см)
Тогда площадь:
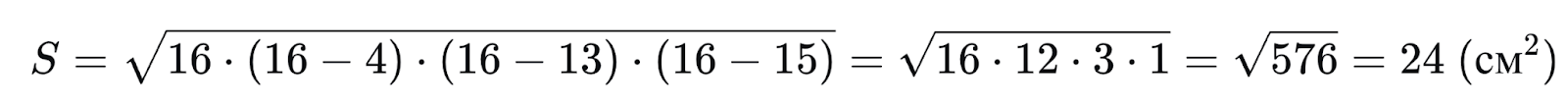
Используем формулу радиуса через стороны и площадь:
R = abc / 4S
R = (4 × 13 × 15) / (4 × 24) = 780 / 96 = 8,125 (см)
Ответ: 8,125 см
Задача 4
Найдите сторону правильного треугольника, если радиус описанной около него окружности равен 10 см.
Решение и ответ к задаче 4
Для равностороннего треугольника радиус описанной окружности и сторона связаны формулой:
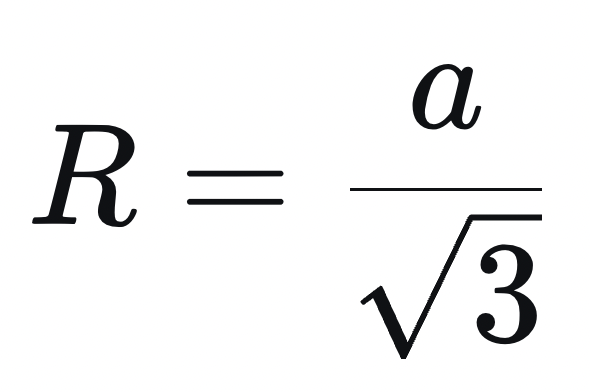
Выразим сторону:
a = R√3
a = 10√3 (см)
Ответ: 10√3 см
Задача 5
Около правильного шестиугольника описана окружность. Сторона шестиугольника равна 8 см. Найдите радиус этой окружности.
Решение и ответ к задаче 5
Для правильного n-угольника радиус описанной окружности выражается через сторону по формуле:
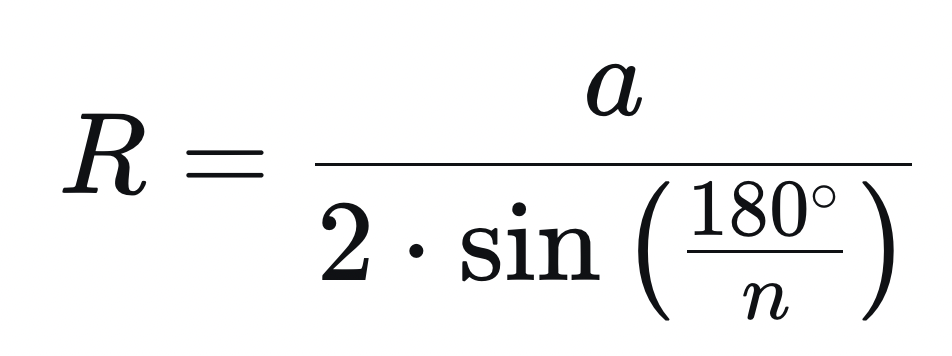
Для шестиугольника n = 6:
sin(180°/6) = sin(30°) = 1/2
Подставляем значения в формулу:
R = 8 / (2 * (1/2)) = 8 / 1 = 8 (см)
Ответ: 8 см
Популярные вопросы и ответы
Отвечает Артем Островский, преподаватель курсов программирования и машинного обучения Московского физико-технического института, куратор заочной физико-технический школы МФТИ по физике и математике:
Как связаны между собой радиусы вписанной и описанной окружностей в прямоугольном треугольнике?
С радиусом описанной окружности все довольно просто. Прямой угол, равный 90°, в прямоугольном треугольнике опирается на дугу в 180°, то есть на диаметр окружности. Поэтому сторона, лежащая против прямого угла, — гипотенуза c, является диаметром описанной окружности. Отсюда следует простая формула: R = c / 2.
С радиусом вписанной окружности ситуация чуть менее очевидна, но тоже достаточно простая. Площадь любого треугольника можно выразить как произведение радиуса вписанной окружности на полупериметр: S = r × (a + b + c) / 2, где r — радиус вписанной окружности. С другой стороны, площадь прямоугольного треугольника равна S = ab / 2, где a и b — катеты.
Приравнивая эти выражения для площади и сокращая, получаем формулу радиуса вписанной окружности: r = (a + b − c) / 2.
Таким образом, радиусы вписанной и описанной окружностей в прямоугольном треугольнике напрямую связаны между собой. Поскольку R = c / 2, а r = (a + b — c) / 2, их сумму можно выразить через катеты: r + R = (a + b) / 2. Это означает, что сумма радиусов вписанной и описанной окружностей равна среднему арифметическому длин катетов.
С радиусом вписанной окружности ситуация чуть менее очевидна, но тоже достаточно простая. Площадь любого треугольника можно выразить как произведение радиуса вписанной окружности на полупериметр: S = r × (a + b + c) / 2, где r — радиус вписанной окружности. С другой стороны, площадь прямоугольного треугольника равна S = ab / 2, где a и b — катеты.
Приравнивая эти выражения для площади и сокращая, получаем формулу радиуса вписанной окружности: r = (a + b − c) / 2.
Таким образом, радиусы вписанной и описанной окружностей в прямоугольном треугольнике напрямую связаны между собой. Поскольку R = c / 2, а r = (a + b — c) / 2, их сумму можно выразить через катеты: r + R = (a + b) / 2. Это означает, что сумма радиусов вписанной и описанной окружностей равна среднему арифметическому длин катетов.
Как изменится радиус описанной окружности, если все стороны треугольника увеличить в 3 раза?
Радиус описанной окружности изменится также в 3 раза. Это следует из свойства подобия: при увеличении всех сторон треугольника в k раз (в данном случае k=3) получается подобный ему треугольник. Все линейные элементы подобных фигур, включая радиусы описанной и вписанной окружностей, медианы, биссектрисы и высоты, изменяются с тем же коэффициентом подобия k.
Почему тему по геометрии «Описанная окружность» изучают в 8 классе?
Тему «Описанная окружность» изучают в 8 классе, так как к этому времени у учащихся уже сформирован необходимый фундамент. К восьмому классу школьники последовательно осваивают:
• треугольники и их свойства,
• четырехугольники и их признаки,
• основные понятия, связанные с окружностью.
Именно на этом базисе строится доказательство ключевой теоремы о том, что центр описанной окружности лежит на пересечении серединных перпендикуляров, и выводятся важные следствия, такие как теорема синусов.
Эта тема является обязательной в соответствии с Федеральной рабочей программой по математике2.
• треугольники и их свойства,
• четырехугольники и их признаки,
• основные понятия, связанные с окружностью.
Именно на этом базисе строится доказательство ключевой теоремы о том, что центр описанной окружности лежит на пересечении серединных перпендикуляров, и выводятся важные следствия, такие как теорема синусов.
Эта тема является обязательной в соответствии с Федеральной рабочей программой по математике2.
В каких заданиях ОГЭ и ЕГЭ встречаются задачи на описанную окружность?
В ОГЭ задачи на эту тему чаще всего встречаются в первой части экзамена. Это, как правило, задания на работу с прямоугольным треугольником и описанной окружность, где требуется найти радиус окружности, зная гипотенузу, или наоборот. Встречаются задачи на свойство вписанного угла, опирающегося на диаметр (такой угол всегда прямой). Могут быть простые расчеты, связывающие стороны треугольника с радиусами вписанной или описанной окружности.
В ЕГЭ профильного уровня задачи могут встречаться как в первой, так и во второй (сложной) части. В первой части это обычно прямые вычисления по формулам: найти радиус R по сторонам треугольника или используя теорему синусов. Во второй части (например, в планиметрической задаче) описанная окружность часто выступает как ключевой элемент. С ее помощью доказывают равенства углов, находят отношения сторон или площади фигур, комбинируя ее свойства с другими геометрическими теоремами.
Для успешной подготовки к таким заданиям рекомендуется активно использовать задания из Открытого банка ФИПИ,3 где можно найти множество прототипов экзаменационных задач по этой теме.
В ЕГЭ профильного уровня задачи могут встречаться как в первой, так и во второй (сложной) части. В первой части это обычно прямые вычисления по формулам: найти радиус R по сторонам треугольника или используя теорему синусов. Во второй части (например, в планиметрической задаче) описанная окружность часто выступает как ключевой элемент. С ее помощью доказывают равенства углов, находят отношения сторон или площади фигур, комбинируя ее свойства с другими геометрическими теоремами.
Для успешной подготовки к таким заданиям рекомендуется активно использовать задания из Открытого банка ФИПИ,3 где можно найти множество прототипов экзаменационных задач по этой теме.
Источники
Материал подготовлен на основании официальных документов и рекомендаций:
1. Министерство просвещения России. Федеральный перечень учебников. URL: https://fpu.edu.ru/
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. «Геометрия. 7-9 классы. Базовый уровень»
- Смирнов В.А., Смирнова И.М. «Геометрия. 7 класс»
- Смирнов В.А., Смирнова И.М. «Геометрия. 8 класс»
- Смирнов В.А., Смирнова И.М. «Геометрия. 9 класс»
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. «Геометрия. 10-11 классы. Базовый и углубленный уровни»
- Мерзляк А.Г., Номировский Д.А., Поляков В.М. «Геометрия. 10 класс. Углубленный уровень»
- Мерзляк А.Г., Номировский Д.А., Поляков В.М. «Геометрия. 11 класс. Углубленный уровень»
2. Министерство просвещения России. Федеральная рабочая программа по учебному предмету «Математика». URL: https://static.edsoo.ru/projects/fop/index.html#/sections/200215
3. Федеральный институт педагогических измерений. Открытый банк заданий ОГЭ и ЕГЭ по математике. Методические рекомендации для учителей. URL: https://fipi.ru
