Показательные неравенства
Показательные неравенства: что такое и как решать. Пошагово разбираем все методы решения, учимся избегать частых ошибок и применяем знания на практике

Представьте, что вы наблюдаете за стремительным ростом числа зараженных во время эпидемии или за распадом радиоактивного вещества. Все эти процессы описываются показательной функцией, а чтобы их анализировать и прогнозировать, необходимо уметь работать с показательными неравенствами. Это важный инструмент для сравнения скоротечных изменений в науке, экономике и IT.
В отличие от линейных и квадратных неравенств, здесь переменная находится не в основании степени, а в ее показателе — это и определяет особые правила и методы их решения.
Что такое показательные неравенства в алгебре
Показательное неравенство — это неравенство, в котором неизвестная переменная содержится в показателе степени.
В таких неравенствах всегда сравниваются:
- показательная функция и число
- две показательные функции
Знаком сравнения может быть любой из символов: >, <, ≥, ≤.
Выделяют три основных вида показательных неравенств.
Простейшие показательные неравенства
Неравенства, где с одной стороны неравенства стоит показательная функция, а с другой — число.
af(x) > b,
где:
- a — основание степени, положительное число, не равное 1 (a > 0, a ≠ 1),
- f(x) — выражение, зависящие от переменной x,
- b — заданное число.
Пример: 2(x + 1) > 8
Стандартные показательные неравенства
Неравенства, где сравниваются две степени, основания которых могут быть равны или приводиться к одному значению.
af(x) > ag(x),
где:
- a — основание степени, положительное число, не равное 1 (a > 0, a ≠ 1),
- f(x) и g(x) — выражения, зависящие от переменной x.
Пример: 9x ≤ 27(x — 1)
Показательно-степенные неравенства
Неравенства, где переменная есть и в основании, и в показателе степени.
f(x)g(x) > f(x)h(x),
где:
- f(x), g(x) и h(x) — выражения, зависящие от переменной x (f(x) > 0).
Пример: (3x — 1)(x — 5) > 1
Полезная информация о показательных неравенствах
Поняв общую классификацию показательных неравенств, полезно запомнить несколько ключевых характеристик, которые определяют подход к решению всех типов показательных неравенств. Эти свойства объясняют, почему методы решения работают именно так, а не иначе.
| Характеристика показательных неравенств | Описание |
|---|---|
| Область определения | Основание степени a > 0, a ≠ 1; показатель степени может быть любым действительным числом |
| Монотонность | При a>1 функция возрастает, при 0<a<1 — убывает. Это определяет правило смены знака неравенства |
| Частые ошибки при решении | Неучет ОДЗ основания, неправильная смена знака при 0 < a < 1, логарифмирование отрицательных чисел |
Что такое решение неравенства
Решить показательное неравенство — значит найти все значения переменной x, при которых неравенство становится верным.
В отличие от показательных уравнений, которые часто имеют конечное число корней, решения показательных неравенств обычно представляют собой бесконечное множество значений — числовой промежуток или объединение нескольких промежутков.
Рассмотрим два примера:
- Уравнение 3x = 9 → x = 2
- Неравенство 3x > 9 → x > 2 → x ∈ (2; +∞)
Типы решений неравенств
Результат показательного неравенства может быть записан различными способами. Существует три основные формы записи решений.
1. Запись в виде неравенства. Является самым простым способом представить решение. Типы записи:
- x > a, x < a — строгий ответ
- x ≥ a, x ≤ a — нестрогий ответ
- a < x < b, a ≤ x ≤ b, a < x ≤ b, a ≤ x < b — двойное неравенств
Примеры:
3(x + 1) ≥ 9 → x ≥ 1
2 < 2x < 8 → 1 < x < 3
2. Запись в виде числового промежутка. Является более формальной математической записью.
Типы промежутков:
- (a; b) — интервал (a < x < b)
- (a; b] — полуинтервал (a < x ≤ b)
- [a; b) — полуинтервал (a ≤ x < b)
- [a; b] — отрезок (a ≤ x ≤ b)
- (-∞; a) — открытый луч (x < a)
- (a; +∞) — открытый луч (x > a)
- (-∞; a] — закрытый луч (x ≥ a)
- [a; +∞) — закрытый луч (x ≥ a)
Примеры:
5x < 125 → x ∈ (-∞; 3)
2(x-2) ≥ ½ → x ∈ [1; +∞)
3. Графическое представление. Наглядный способ изображения решения на числовой прямой.
Правила обозначений:
- ● — точка включается (для знаков ≥ или ≤)
- ○ — точка не включается (для знаков > или <)
- → или ← — направление решения
Примеры:
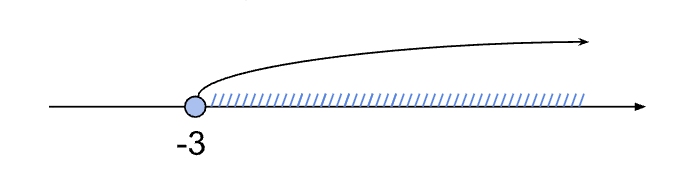
4(-x) ≤ 64 → x ∈ [-3; +∞)
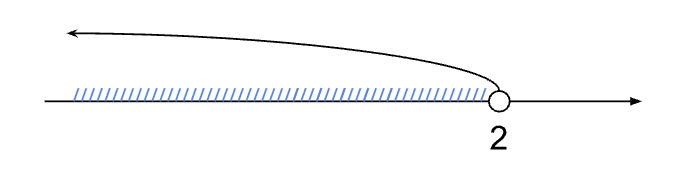
2(2x — 3) < 2 → x ∈ (-∞; 2)
Все три формы записи решений являются равнозначными и используются в зависимости от конкретной задачи или требований. В школьной практике часто требуется представлять решение всеми тремя способами.

Методы решения показательных неравенств
Для решения показательных неравенств используется несколько ключевых методов, выбор которых зависит от вида неравенства. Все они делятся на три основные типа.
Методы логарифмирования и приведения к одному основанию для неравенств вида af(x) > b (или <, ≥, ≤)
Алгоритм решения:
1. Проанализируйте правую часть неравенства b.
Если b ≤ 0:
- неравенство af(x) > b (или ≥ b) верно при всех x,
- неравенство af(x) < b (или ≤ b) не имеет решений.
Если b > 0, переходите к шагу 2.
2. Сравните показатель степени f(x) со специальным значением: нам нужно найти такое число, при подстановке которого вместо f(x) выполняется равенство af(x) = b. Выберите один из двух способов перехода к более простому неравенству.
- Логарифмирование. Прологарифмируйте число b по основанию a.
Ключевой момент: значение основания a определяет, сохранится ли знак неравенства или изменится.
Если a > 1, знак неравенства сохраняется:
af(x) > b ⇔ f(x) > logab
af(x) < b ⇔ f(x) < logab
Если 0 < a < 1, знак неравенства меняется на противоположный:
af(x) > b ⇔ f(x) < logab
af(x) < b ⇔ f(x) > logab
- Приведение к одному основанию. Подберите такую степень c, чтобы ac = b.
Исходное неравенство принимает вид: af(x) > ac. Значение основания степени a влияет на сохранение или изменение знака неравенства. Если а > 1, знак неравенства сохраняется:
af(x) > b ⇔ f(x) > c
af(x) < b ⇔ f(x) < c
Если 0 < a < 1, знак неравенства меняется на противоположный:
af(x) > b ⇔ f(x) < c
af(x) < b ⇔ f(x) > c
3. Решите полученное неравенство относительно x.
Примеры
Решим неравенство: 3(x+2) < 81.
Основание 3 > 1, значит, знак сохраняется:
x + 2 < log381
Так как 81 = 34, то log381 = 4.
Получаем: x + 2 < 4 → x < 2.
Ответ: x ∈ (-∞; 2)
Решим неравенство: (½)(2x-1) ≥ 4.
Основание 0 < ½ < 1, значит, знак меняется на противоположный:
2x — 1 ≤ log ½4
Так как 4 = (½)-2, то log½4 = -2.
Получаем: 2x — 1 ≤ -2 → 2x ≤ -1 → x ≤ -0,5.
Ответ: x ∈ (-∞; -0,5]
Решим неравенство: 5x > -10
Выражение 5x всегда положительно, а число -10 отрицательно. Положительное число всегда больше отрицательного. Следовательно, неравенство верно при любом x.
Формально, по алгоритму: основание 5 > 1, знак сохраняется: x > log5(-10). Но логарифм от отрицательного числа не определен. Это сигнализирует о том, что классический метод не нужен, а ответ — все действительные числа.
Ответ: x ∈ x ∈ (-∞; +∞)
Метод сравнения показателей степени для неравенств вида af(x) > ag(x) (или <, ≥, ≤)
Этот метод является частным случаем предыдущего, где b = ag(x). Алгоритм решения:
- Убедитесь, что основания равны. Если основания не равны, представьте все степени в неравенстве как степени с одним основанием, используя свойства степеней.
- Сравните показатели, учитывая основание a. Если a > 1, знак неравенства сохраняется: af(x) > ag(x) ⇔ f(x) > g(x).
Если 0 < a < 1, знак неравенства меняется на противоположный:
af(x) > ag(x) ⇔ f(x) < g(x). - Решите полученное неравенство относительно x.
Примеры
Решим неравенство: 5(3x — 1) > 5(x + 2).
Основание 5 > 1, знак сохраняется.
Переходим к показателям: 3x — 1 > x + 2.
Решаем: 3x — x > 2 + 1 → 2x > 3 → x > 1,5.
Ответ: x ∈ (1,5; +∞)
Решим неравенство: 9(x+1) ≤ 27(x-2).
Приводим обе части к основанию 3:
9(x+1) = (32)(x+1) = 3(2x + 2)
27(x-2) = (33)(x-2) = 3(3x — 6)
Получаем: 3(2x + 2) ≤ 3(3x — 6)
Основание 3 > 1, знак сохраняется.
Переходим к показателям: 2x + 2 ≤ 3x — 6.
Решаем: 2x — 3x ≤ -6 — 2 → -x ≤ -8 → x ≥ 8.
Ответ: x ∈ [8; +∞)
Метод замены переменной для неравенств с повторяющимся выражением af(x)
Этот метод является универсальным приемом для упрощения сложных показательных неравенств, которые сводятся к алгебраическим, чаще всего квадратным. Данный способ работает для тех неравенств, в которых можно выделить повторяющееся выражение af(x). Алгоритм решения:
- Преобразуйте неравенство, чтобы выделить повторяющееся выражение вида af(x).
- Введите новую переменную. Чаще всего заменяют t = af(x). Важно: поскольку af(x) > 0, то t > 0.Решите полученное алгебраическое
- неравенство относительно t с учетом условия t > 0.
- Вернитесь к исходной переменной, подставив t в замену.
- Решите полученное простейшее показательное неравенство.
Примеры
Решим неравенство: 4x — 3 × 2x — 4 > 0.
Преобразуем: 4x — 3 × 2x — 4 > 0 → (2 × 2)x — 3 × 2x — 4 > 0 → 22x — 3 × 2x — 4 > 0.
Выполним замену: t = 2x, t > 0.
Получаем: t2 — 3t — 4 > 0 — квадратное неравенство.
Решаем полученное выражение любым способом решения квадратных неравенств и получаем решение: t < -1 и t > 4.
Учитывая, что t > 0, остается t > 4
Возвращаемся обратно к переменной x: 2x > 4
Решаем простейшее неравенство: 2x > 4 → 2x > 22 → x > 2.
Ответ: x ∈ (2; +∞)
Решим неравенство: 5(x + 1) + 5(2 — x) > 30.
Используем свойства степеней:
5(x + 1) = 5 × 5x
5(2 — x) = 25/5x
Неравенство принимает вид: 5 × 5x + 25/5x > 30.
Выполним замену: t = 5x, t > 0.
Получаем: 5t + 25/t > 30 — дробно-рациональное неравенство.
Перенесем все слагаемые в левую часть и приведем к общему знаменателю:
5t2/t + 25/t — 30t/t > 0.
Домножаем полученное неравенство на неизвестную t. Мы можем выполнить данное действие, так как по условию t > 0, знак неравенства остается неизменным.
Получаем: 5t2 + 25 — 30t > 0.
Решаем полученное выражение любым способом решения квадратных неравенств и получаем решение: t < 1 и t > 5.
Учитывая, что t > 0, остается 0 < t < 1 и t > 5.
Возвращаемся обратно к переменной x и решаем два простейших неравенства:
0 < 5x < 1 → 5x < 50 → x < 0
5x > 5 → 5x > 51 → x > 1
Оба решения входят в ответ.
Ответ: x ∈ (-∞; 0) ∪ (1; +∞)
Классический метод для неравенств вида f(x)g(x) > f(x)h(x) (или <, ≥, ≤)
Алгоритм решения:
- Найдите область допустимых значений (ОДЗ): основание степени должно быть строго положительным: f(x) > 0.
- Разберите два случая:
f(x) > 1, знак неравенства сохраняется: f(x)g(x) > f(x)h(x) ⇔ g(x) > h(x).
0 < f(x) < 1, знак неравенства меняется на противоположный:
f(x)g(x) > f(x)h(x) ⇔ g(x) < h(x). - Решите системы неравенств для каждого случая, учитывая их условия.
- Если исходное неравенство строгое (> или <), то значения x, в которых f(x) = 1, не включатся в ответ. Если неравенство нестрогое (≥ или ≤), то точки, в которых f(x) = 1 включаются в ответ.
- Объедините решения, найденные в первом и во втором случаях, а также, при необходимости, граничные точки.
- Определите решения, удовлетворяющие ОДЗ.
Примеры
Решим неравенство: (x — 2)(x + 1) > 1.
ОДЗ: x — 2 > 0 → x > 2
Заметим, что справа стоит 1, единицу можно представить в виде (x — 2)0.
Неравенство принимает вид: (x — 2)(x + 1) > (x — 2)0. При x — 2 > 1 знак сохраняется: x + 1 > 0.
Решаем систему двух неравенств:
x — 2 > 1 → x > 3
x + 1 > 0 → x > -1
Объединяем x > 3 и x > -1: x ∈ (3; +∞).
При 0 < x — 2 < 1 знак меняется на противоположный: x + 1 < 0.
Решаем систему двух неравенств:
0 < x — 2 < 1 → 2 < x < 3
x + 1 < 0 → x < -1
Объединяем 2 < x < 3 и x < -1: x ∈ ∅
Так как исходное неравенство строгое, то точка, в которой x — 2 = 1 → x = 3, не включается в ответ.
Объединяем решения двух случаев, учитывая ОДЗ: x ∈ (3; +∞)
Ответ: x ∈ (3; +∞)
Решим неравенство: (x + 1)(2x — 5) ≥ (x + 1)(x — 1)
ОДЗ: x + 1 > 0 → x > -1
При x + 1 > 1 знак сохраняется: 2x — 5 ≥ x -1.
Решаем систему двух неравенств:
x + 1 > 1 → x > 0
2x — 5 ≥ x -1 → x ≥ 4
Объединяем x > 0 и x ≥ 4: x ∈ [4; +∞).
При 0 < x + 1 < 1 знак меняется на противоположный: 2x — 5 ≤ x -1.
Решаем систему двух неравенств:
0 < x + 1 < 1 → -1 < x < 0
2x — 5 ≤ x -1 → x ≤ 4
Объединяем -1 < x < 0 и x ≤ 4: x ∈ (−1; 0).
Так как исходное неравенство нестрогое, то точка, в которой x + 1 = 1 → x = 0, включается в ответ.
Объединяем решения двух случаев и граничную точку, учитывая ОДЗ: x ∈ (-1; 0] ∪ [4; +∞).
Ответ: x ∈ (-1; 0] ∪ [4; +∞)
Метод рационализации для неравенств вида f(x)g(x) > f(x)h(x) (или <, ≥, ≤)
Алгоритм решения:
- Найдите ОДЗ: основание степени должно быть строго положительным: f(x) > 0.
- Перенесите все слагаемые в одну сторону: f(x)g(x) — f(x)h(x) > 0.
- Замените неравенство на равносильное:
f(x)g(x) — f(x)h(x) > 0 ⇔ (f(x) — 1)(g(x) — h(x)) > 0. - Решите полученное алгебраическое неравенство.
- Если исходное неравенство строгое (> или <), то значения x, в которых f(x) = 1, не включаются в ответ. Если неравенство нестрогое (≥ или ≤), то точки, в которых f(x) = 1, включаются в ответ.
- Определите решения, удовлетворяющие ОДЗ.
Примеры
Решим неравенство: (x — 2)(x + 1) > 1.
ОДЗ: x — 2 > 0 → x > 2
Заметим, что справа стоит 1, единицу можно представить в виде (x — 2)0.
Неравенство принимает вид: (x — 2)(x + 1) > (x — 2)0.
Переносим значение из правой части в левую: (x — 2)(x + 1) — (x — 2)0 > 0.
Применяем рационализацию: ((x — 2) — 1)((x + 1) — 0) > 0.
Решаем неравенство методом интервалов:
((x — 2) — 1)((x + 1) — 0) > 0 → (x — 3)(x+1) > 0 → x ∈ (−∞; −1) ∪ (3; +∞).
Так как исходное неравенство строгое, то точка, в которой x — 2 = 1 → x = 3, не включается в ответ.
Накладываем на полученное решение ОДЗ: x ∈ (3; +∞).
Ответ: x ∈ (3; +∞)
Решим неравенство: (x + 1)(2x — 5) ≥ (x + 1)(x — 1)
ОДЗ: x + 1 > 0 → x > -1
Переносим значение из правой части в левую: (x + 1)(2x — 5) — (x + 1)(x — 1) ≥ 0.
Применяем рационализацию: ((x + 1) — 1)((2x — 5) — (x — 1)) ≥ 0.
Решаем неравенство методом интервалов:
((x + 1) — 1)((2x — 5) — (x — 1)) ≥ 0 → x(x — 4) ≥ 0 → x ∈ (−∞; 0] ∪ [4; +∞).
Так как исходное неравенство нестрогое, то точка, в которой x + 1 = 1 → x = 0, включается в ответ.
Накладываем на полученное решение ОДЗ: x ∈ (−1; 0] ∪ [4; +∞).
Ответ: x ∈ (−1; 0] ∪ [4; +∞)
Системы показательных неравенств
Системы показательных неравенств — это набор из двух или более неравенств, которые должны выполняться одновременно для одних и тех же значений переменной. Система может содержать только однотипные неравенства — показательные, так и разнотипные — сочетать показательные неравенства с линейными, квадратными, дробно-рациональными и другими типами неравенств.
Алгоритм:
- Решить каждое неравенство отдельно любым методом.
- Найти пересечение всех решений — общую область, где выполняются все неравенства системы одновременно.
При решении систем с разнотипными неравенствами особенно внимательно нужно учитывать области определения каждого неравенства и находить их общую часть.
Примеры
Решим систему неравенств:
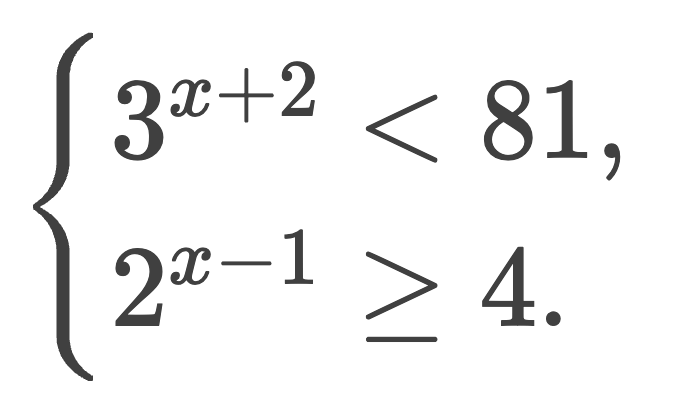
Решаем первое неравенство: 3(x + 2) < 81 → 3(x + 2) < 34 → x + 2 < 4 → x < 2.
Решаем второе неравенство: 2(x — 1) ≥ 4 → 2(x — 1) ≥ 22 → x — 1 ≥ 2 → x ≥ 3.
Находим пересечение x < 2 и x ≥ 3. Общих решений нет.
Ответ: x ∈ ∅
Решим систему неравенств:
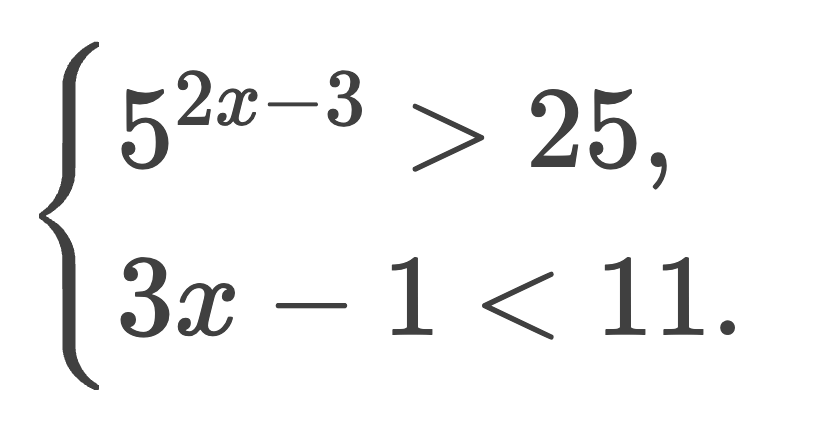
Решаем первое неравенство: 5(2x — 3) > 25 → 5(2x — 3) > 52 → 2x — 3 > 2 → x > 2,5.
Решаем второе неравенство: 3x — 1 < 11 → x < 4.
Находим пересечение x > 2,5 и x < 4. Общее решение: x ∈ (2,5; 4).
Ответ: x ∈ (2,5; 4)
Задачи по теме «Показательные неравенства»
Закрепите изученные методы на практике. Попробуйте решить эти задачи, подобрав для каждой подходящий способ решения. Не забывайте про ОДЗ и правило смены знака.
Задача 1
Решите неравенство: 2(x + 3) > 16.
Задача 2
Решите неравенство: ½(3x — 5) ≤ ½(x + 7).
Задача 3
Решите неравенство: (2x — 4)(x+1) < (2x — 4)(3x — 5).
Задача 4
Решите неравенство: 9x − 4 × 3x + 3 ≥ 0.
Задача 5
Решите систему:
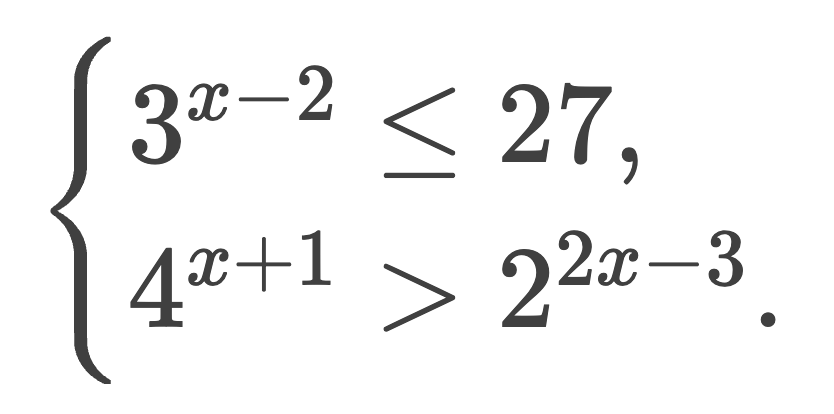
Ответы к задачам
Сверьте свои решения и ответы. Если что-то не сходится — вернитесь к соответствующему методу и разберитесь в ошибке.
Задача 1
Решим неравенство: 2(x + 3) > 16.
Основание 2 > 1, значит, знак сохраняется: x + 3 > log216.
Так как 16 = 24, то log216 = 4.
Получаем: x + 3 > 4 → x > 1.
Ответ: x ∈ (1; +∞)
Задача 2
Решим неравенство: ½(3x — 5) ≤ ½(x + 7)
Основание 0 < ½ < 1, знак меняется на противоположный.
Переходим к показателям: 3x — 5 ≤ x + 7.
Решаем: 3x — x ≤ 7 + 5 → 2x ≤ 12 → x ≤ 6
Ответ: x ∈ (-∞; 6]
Задача 3
Решим неравенство: (2x — 4)(x+1) < (2x — 4)(3x — 5)
ОДЗ: 2x — 4 > 0 → x > 2
Переносим значение из правой части в левую: (2x — 4)(x+1) — (2x — 4)(3x — 5) < 0.
Применяем рационализацию: ((2x — 4) — 1)((x + 1) — (3x — 5)) < 0.
Решаем неравенство методом интервалов:
((2x — 4) — 1)((x + 1) — (3x — 5)) < 0→ (2x — 5)(-2x + 6) < 0 → x ∈ (−∞; 2,5) ∪ (3; +∞).
Так как исходное неравенство строгое, то точка, в которой 2x — 4 = 1 → x = 2,5, не включается в ответ.
Накладываем на полученное решение ОДЗ: x ∈ (2; 2,5) ∪ (3; +∞).
Ответ: x ∈ (2; 2,5) ∪ (3; +∞)
Задача 4
Решим неравенство: 9x − 4 × 3x + 3 ≥ 0.
Преобразуем: 9x − 4 × 3x + 3 ≥ 0 → (3 × 3)x — 4 × 3x + 3 ≥ 0 → 32x — 4 × 3x + 3 > 0.
Выполним замену: t = 3x, t > 0.
Получаем: t2 — 4t + 3 ≥ 0 — квадратное неравенство.
Решаем полученное выражение любым способом решения квадратных неравенств и получаем решение: t ≤ 1 и t ≥ 3.
Учитывая, что t > 0, остается 0 < t ≤ 1 и t ≥ 3.
Возвращаемся обратно к переменной x и решаем два простейших неравенства:
0 < 3x ≤ 1 → 3x ≤ 30 → x ≤ 0
3x ≥ 3 → 3x ≥ 31 → x ≥ 1
Оба решения входят в ответ.
Ответ: x ∈ (-∞; 0] ∪ [1; +∞)
Задача 5
Решаем первое неравенство: 3(x — 2) ≤ 27 → 3(x — 2) ≤ 33 → x — 2 ≤ 3 → x ≤ 5.
Решаем второе неравенство: 4(x + 1) > 2(2x — 3) → 22(x + 1) > 2(2x — 3) → 2(x + 1) > (2x — 3) → 2x + 2 > 2x — 3 → 2 > -3 — верно при всех x.
Так как решение первого неравенства x ≤ 5, а второго любое значение x, то общее решение: x ∈ (-∞; 5].
Ответ: x ∈ (-∞; 5]
Популярные вопросы и ответы
Отвечает Ольга Комарова, учитель математики:
Как меняется знак в показательных неравенствах?
Почему показательные неравенства изучают в 10–11 классах?
В каких заданиях ЕГЭ по математике понадобится умение решать показательные неравенства?
В первую очередь, показательные неравенства могут попасться в задании №13 и №15, которые нацелены на решение уравнений и неравенств, включая показательные и логарифмические. Также этот тип неравенств может встречаться и в задачах с параметрами — задание №18, особенно если нужно рассуждать, при каких условиях выражение становится больше или меньше заданного значения.
Важно отметить, что в базовом ЕГЭ показательные неравенства не встречаются. А вот в профильном уровне они считаются частью обязательной алгебраической подготовки, и решение таких неравенств входит в компетенцию, обозначенную как «уметь решать уравнения и неравенства» (см. спецификацию КИМ ЕГЭ 2025 профильного уровня, табл. 3).
Таким образом, умение решать показательные неравенства — это не просто отдельная тема, это билет в понимание целого класса задач: от алгебры до параметров и даже математического анализа. Без нее невозможно уверенно чувствовать себя на профильном экзамене. Кроме того, умение работать с такими неравенствами помогает избежать потерь баллов там, где важно правильно обосновать переход от одного шага к другому. То есть это не просто задача на технику, это проверка на понимание.