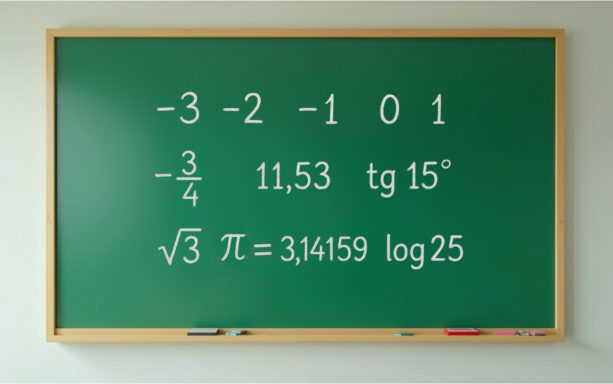Прямоугольная система координат
Прямоугольная система координат — это основа аналитической геометрии, позволяющая точно определять положение точек на плоскости. Как она устроена и как с ней работать? Разберем основные элементы, правила и применение в задачах
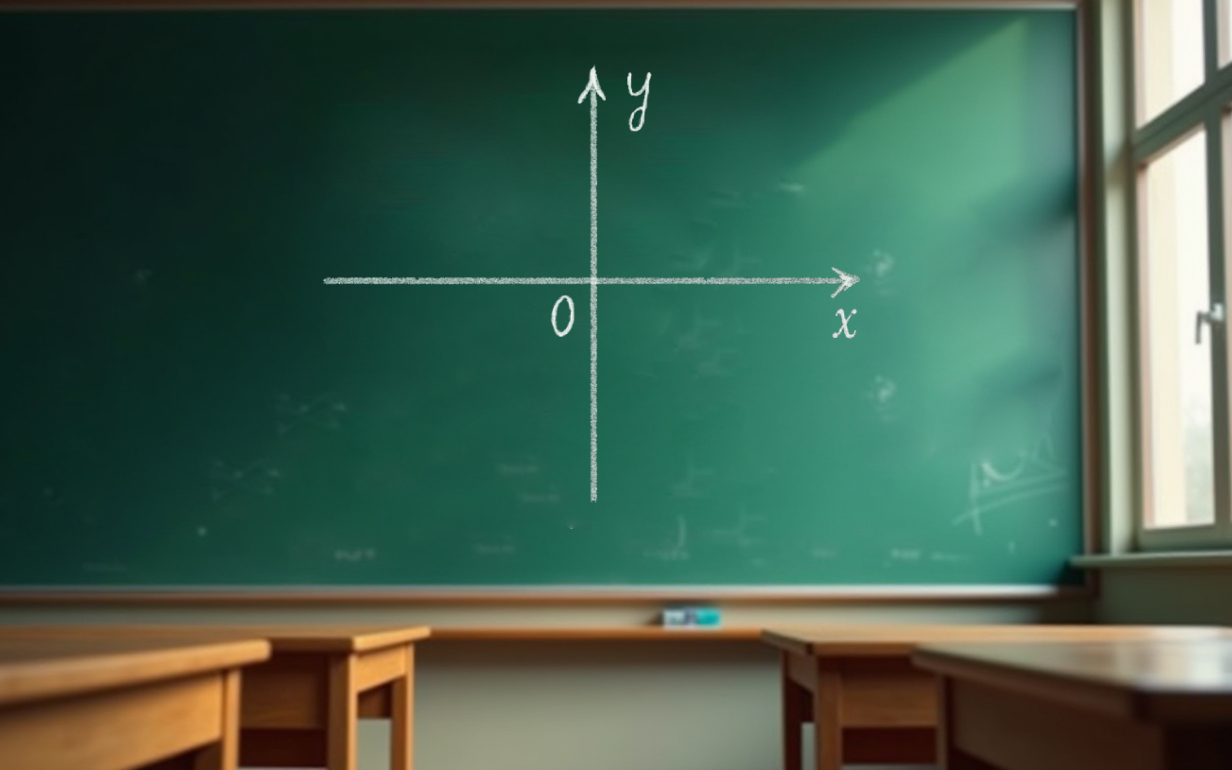
Прямоугольная система координат — это удивительный мост между алгеброй и геометрией, который открыл новые возможности для решения математических задач. Благодаря системе координат мы можем описывать положение точек с помощью чисел, преобразовывать геометрические задачи в алгебраические, строить точные графики функций и решать сложные пространственные задачи.
Прямоугольные координаты используются повсеместно: от школьных уроков математики до сложных инженерных расчетов, от компьютерной графики до систем навигации. Разберем подробно, как устроена эта система, научимся правильно определять координаты точек и применять эти знания на практике.
Что такое прямоугольная система координат в математике
Прямоугольная система координат (декартова система координат) — это система, состоящая из двух взаимно перпендикулярных осей — координатных прямых: горизонтальной и вертикальной.
Горизонтальную ось принято называть ось абсцисс, или OX, вертикальную — ось ординат, или OY. Точка пересечения осей называется началом координат и обозначается как O(0; 0).
Координатные прямые OX и OY обладают всеми свойствами числовых прямых: имеют положительное и отрицательное направление, разбиты на равные единичные отрезки и бесконечны в обоих направлениях.
Любая точка на плоскости задается парой чисел (x; y), где:
- x — координата по оси OX (абсцисса),
- y — координата по оси OY (ордината).
Полезная информация о прямоугольной системе координат
Прежде чем работать с прямоугольной системой координат, важно разобраться с ее основными составляющими. В таблице ниже собраны все базовые элементы, которые необходимо знать для уверенной работы с координатной плоскостью.
| Элемент прямоугольной системы координат | Описание |
|---|---|
| Ось OX (ось абсцисс) | Горизонтальная числовая прямая. Положительные значения откладываются вправо от начала координат, отрицательные — влево |
| Ось OY (ось ординат) | Вертикальная числовая прямая. Положительные значения откладываются вверх от начала координат, отрицательные — вниз |
| Начало координат O | Точка пересечения осей с координатами (0; 0). Является точкой отсчета для всех измерений на плоскости |
| Координаты точки (x; y) | Пара чисел, определяющая положение точки, где: x — расстояние по горизонтали от точки до оси OY с учетом знакаy — расстояние по вертикали от точки до оси OX с учетом знака |
| Четверти плоскости | Четыре области, на которые оси делят плоскость |
Оси прямоугольной системы координат
Оси координат — это элементы системы, представляющие собой координатные прямые, которые задают основу для измерения и определения положения точек на плоскости. Оси пересекаются под прямым углом и в точке пересечения образуют начало координат.
Ось абсцисс
Ось абсцисс, обозначаемая как OX, представляет собой горизонтальную координатную прямую, которая является основой для отсчета положения точек по горизонтали. Эта ось перпендикулярна оси OY и проходит через начало координат, деля плоскость на верхнюю и нижнюю половины.
Ключевые характеристики оси OX:
- расположена горизонтально,
- положительное направление — вправо от начала координат,
- отрицательное направление — влево от начала координат,
- служит для определения абсциссы точек — x-координаты.
Ось ординат (OY)
Ось ординат, обозначаемая как OY, представляет собой вертикальную координатную прямую, которая определяет положение точек по вертикали. Эта ось перпендикулярна оси OX и также проходит через начало координат, деля плоскость на левую и правую половины.
Ключевые характеристики оси OY:
- расположена вертикально,
- положительное направление — вверх от начала координат,
- отрицательное направление — вниз от начала координат,
- служит для определения ординаты точек — y-координаты.
Четверти прямоугольной системы координат
Пересекающиеся оси OX и OY делят координатную плоскость на четыре области, которые называются координатными четвертями. Каждая четверть имеет свой уникальный набор знаков координат и играет важную роль при анализе графиков функций и решении геометрических задач.
Нумерация и характеристики четвертей.
I четверть (верхняя правая)
x > 0 (положительные абсциссы)
y > 0 (положительные ординаты)
Пример: точка A(3; 2)
II четверть (верхняя левая)
x < 0 (отрицательные абсциссы)
y > 0 (положительные ординаты)
Пример: точка B(-4; 1)
III четверть (нижняя левая)
x < 0 (отрицательные абсциссы)
y < 0 (отрицательные ординаты)
Пример: точка C(-2; -3)
IV четверть (нижняя правая)
x > 0 (положительные абсциссы)
y < 0 (отрицательные ординаты)
Пример: точка D(5; -2)
Существуют особые случаи, когда точки не принадлежат ни одной четверти, а именно точки на оси OX (y = 0), точки на оси OY (x = 0) и начало координат (x = 0, y = 0).
это интересно
Пошаговая инструкция по построению точек на координатной плоскости и нахождению их координат
Работа с координатной плоскостью включает два взаимосвязанных процесса: построение точек по заданным координатам и определение координат уже отмеченных точек. Оба навыка необходимы для уверенного владения системой координат.
Алгоритм построения точки по заданным координатам
- Проанализируйте координаты (x; y). Для этого определите знаки обеих координат, установите, в какой четверти должна находиться точка. Запомните: первое число — положение по горизонтали, второе — по вертикали.
- Начните отсчет от начала координат O(0; 0). Важно не забыть проконтролировать масштаб: какие единичные отрезки заданы на каждой числовой прямой.
- Отложите значение по оси OX. Если x > 0, то необходимо двигаться вправо от начала координат, если x < 0 — влево. Отсчитайте ровно |x| единиц вдоль горизонтальной оси.
- Отложите значение по оси OY. Если y > 0, то необходимо двигаться вверх от начала координат, если y < 0 — вниз. Отсчитайте ровно |y| единиц вдоль вертикальной оси.
- Найдите точку пересечения значений, отложенных по оси OX и OY. Отметьте ее, подписав название и координаты.
Алгоритм нахождения координат отмеченной точки
- Найдите начало координат O(0; 0). Определите точку пересечения осей. Уточните масштаб: сколько единиц в одной клетке или делении.
- Определите проекцию точки на ось OX. Мысленно опустите перпендикуляр от искомой точки на горизонтальную ось. Если проекция справа точки O, то x > 0, если слева — x < 0. Посчитайте количество единиц от начала координат до проекции, определив значение координаты x.
- Определите проекцию точки на ось OY. Мысленно опустите перпендикуляр от искомой точки на вертикальную ось. Если проекция выше точки O, то y > 0, если ниже — y < 0. Посчитайте количество единиц от начала координат до проекции, определив значение координаты y.
- Укажите полученные значения с соответствующими знаками в формате (x; y).
Задачи на тему «Прямоугольная система координат»
Пришло время применить знания на практике. Решение задач поможет закрепить понимание системы координат, научиться работать с осями и четвертями, а также избежать распространенных ошибок. Попробуйте решить эти задачи самостоятельно, а затем проверьте свои ответы.
Задача 1
Определите, в каких четвертях координатной плоскости расположены точки:
а) A(2; 5)
б) D(−5; −2)
в) L(0; −1)
г) F(−3; 4)
д) P(4; −3)
Задача 2
Постройте точки на координатной плоскости: F(3; 4), G(−2; 1), H(−1; −3), I(4; −2), J(0; 3).
Задача 3
Определите, на каких осях координат расположены точки:
а) K(0; 4)
б) L(−3; 0)
в) M(0; −2)
г) N(5; 0).
Ответы к задачам
Проверьте свои решения. Если вы где-то ошиблись — не страшно. Проанализируйте ошибки и повторите соответствующий раздел статьи.
Задача 1
а) Точка A(2; 5): x > 0, y > 0 → I четверть
б) Точка D(−5; −2): x < 0, y < 0 → III четверть
в) Точка L(0; −1): x = 0 → лежит на оси OY, не принадлежит ни одной четверти
г) Точка F(−3; 4): x < 0, y > 0 → II четверть
д) Точка P(4; −3): x > 0, y < 0 → IV четверть
Ответ: а) I четверть; б) III четверть; в) лежит на оси OY, не принадлежит ни одной четверти; г) II четверть; д) IV четверть
Задача 2
Задача 3
Точка K(0; 4): x = 0 → лежит на оси OY
Точка L(−3; 0): y = 0 → лежит на оси OX
Точка M(0; −2): x = 0 → лежит на оси OY
Точка N(5; 0): y = 0 → лежит на оси OX
Ответ: а) OY; б) OX; в) OY; г) OX
Популярные вопросы и ответы
Отвечает Артем Островский, преподаватель курсов программирования и машинного обучения Московского физико-технического института:
Как легко запомнить, как читать координаты?
Представьте, что вы заходите в зал в кинотеатре и ищете свое место. На билете указано: ряд 5, место 3. Логично, что сначала нужно найти свой ряд — вертикаль, а уже потом — нужное место, горизонталь.
С координатами точки, например (3; 5), действует абсолютно тот же принцип. Первое число 3 — это x, он же абсцисса. Это ваше движение по горизонтальной оси, словно вы ищете номер своего места. Второе число 5 — это y, он же ордината. Это движение по вертикальной оси, которое указывает на нужный «ряд».
С координатами точки, например (3; 5), действует абсолютно тот же принцип. Первое число 3 — это x, он же абсцисса. Это ваше движение по горизонтальной оси, словно вы ищете номер своего места. Второе число 5 — это y, он же ордината. Это движение по вертикальной оси, которое указывает на нужный «ряд».
Почему прямоугольную систему координат изучают в 6 классе?
К 6 классу ученики уже хорошо знакомы с числами: не только с положительными, но и с отрицательными и дробными. Изучение координатной плоскости становится логичным следующим шагом, который позволяет «увидеть» числа в пространстве. Это как выучить буквы, а потом научиться складывать из них слова. Координатная система — это новый язык, который позволяет описывать положение объектов и связывать алгебру с геометрией.
В каких заданиях ОГЭ и ЕГЭ по математике может понадобиться знание темы «Прямоугольная система координат»?
В ОГЭ это задания с графиками функций: построить график, найти точки пересечения графиков, определить значение функции по графику — все выполняется на координатной плоскости. А также геометрические задачи на клетчатой бумаге: найти расстояние между точками, вычислить длину вектора, найти площадь фигуры — все это также довольно легко решить, если ввести систему координат.
В ЕГЭ:
• задания с функциями (первая часть): вычисление производных, нахождение точек максимума и минимума на графике функции;
• планиметрия (вторая часть, профиль): метод координат — это хороший инструмент для решения геометрических задач, с его помощью можно аналитически найти длины сторон, углы, площади фигур;
• стереометрия (вторая часть, профиль): это «высший пилотаж» — с помощью введения трехмерной системы координат (добавляется ось Z) можно аналитически решать задачи на нахождение углов между прямыми и плоскостями или расстояний в пространстве;
• параметр (вторая часть, профиль): довольно часто решение сводится к анализу взаимного расположения графиков функций в координатной плоскости.
В ЕГЭ:
• задания с функциями (первая часть): вычисление производных, нахождение точек максимума и минимума на графике функции;
• планиметрия (вторая часть, профиль): метод координат — это хороший инструмент для решения геометрических задач, с его помощью можно аналитически найти длины сторон, углы, площади фигур;
• стереометрия (вторая часть, профиль): это «высший пилотаж» — с помощью введения трехмерной системы координат (добавляется ось Z) можно аналитически решать задачи на нахождение углов между прямыми и плоскостями или расстояний в пространстве;
• параметр (вторая часть, профиль): довольно часто решение сводится к анализу взаимного расположения графиков функций в координатной плоскости.
