Центральные и вписанные углы
Разберемся, что такое центральные и вписанные углы, какими свойствами они обладают и как эти знания помогают решать задачи по геометрии
Окружность — одна из самых гармоничных геометрических фигур, а ее изучение было бы неполным без понимания ключевых элементов: центральных и вписанных углов. Именно они образуют «каркас», связывающий дуги, хорды и радиусы в единую систему. Знание их свойств открывает путь к решению множества геометрических задач. В этой статье мы разберем, чем отличаются эти углы, сформулируем их главные свойства и научимся применять теоремы на практике.
Что такое центральные и вписанные углы в геометрии
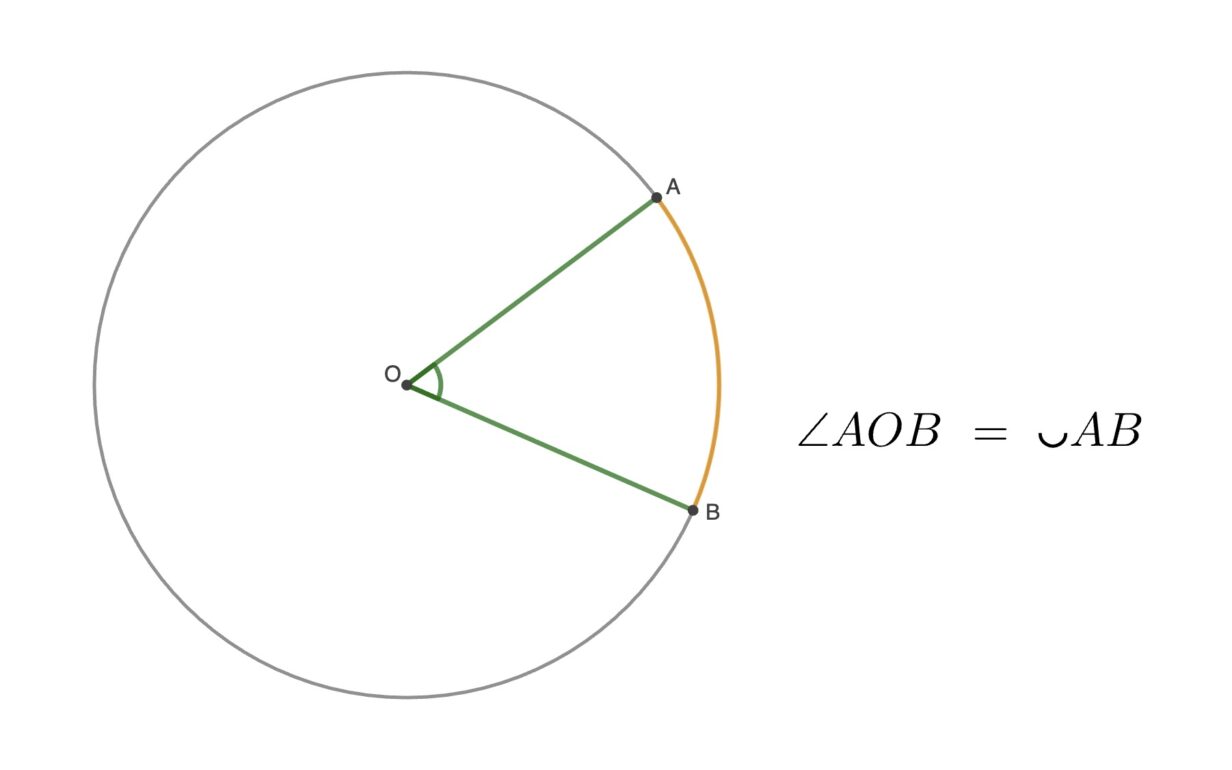
Центральный угол — это угол, вершина которого находится в центре окружности, а стороны являются радиусами.
Стороны центрального угла выделяют на окружности дугу. Говорят, что угол опирается на эту дугу. Центральный угол равен градусной мере дуги, на которую он опирается.
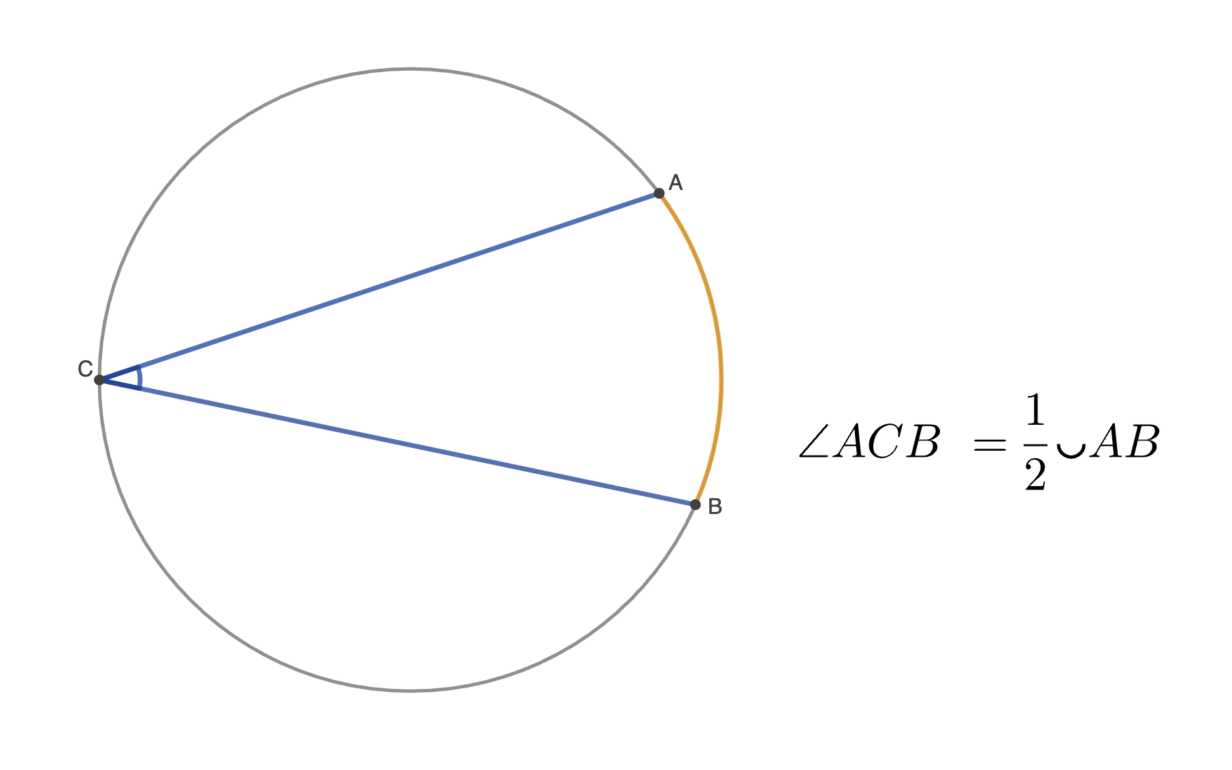
Вписанный угол — это угол, вершина которого лежит на окружности, а стороны являются хордами. Стороны вписанного угла также выделяют на окружности дугу, на которую данный угол опирается.
Вписанный угол равен половине градусной меры дуги, на которую он опирается.
Полезная информация о центральных и вписанных углах
Центральные и вписанные углы — это парные элементы окружности. Их сравнение помогает лучше понять геометрические закономерности. В таблице собраны их ключевые характеристики.
| Центральный угол | Вписанный угол |
|---|---|
| Вершина находится в центре окружности | Вершина лежит на самой окружности |
| Стороны являются радиусами | Стороны являются хордами |
| Градусная мера равна градусной мере дуги, на которую он опирается | Градусная мера равна половине градусной мере дуги, на которую он опирается |
Свойства центральных и вписанных углов
Работа с данными углами строится на нескольких фундаментальных правилах. Мы уже знаем, что центральный угол равен градусной мере дуги, на которую он опирается, а вписанный угол равен половине градусной меры дуги, на которую он опирается. Благодаря этим свойствам строится еще одна важная теорема и два ее следствия, которые открывают путь к решению огромного количества задач.
это интересно
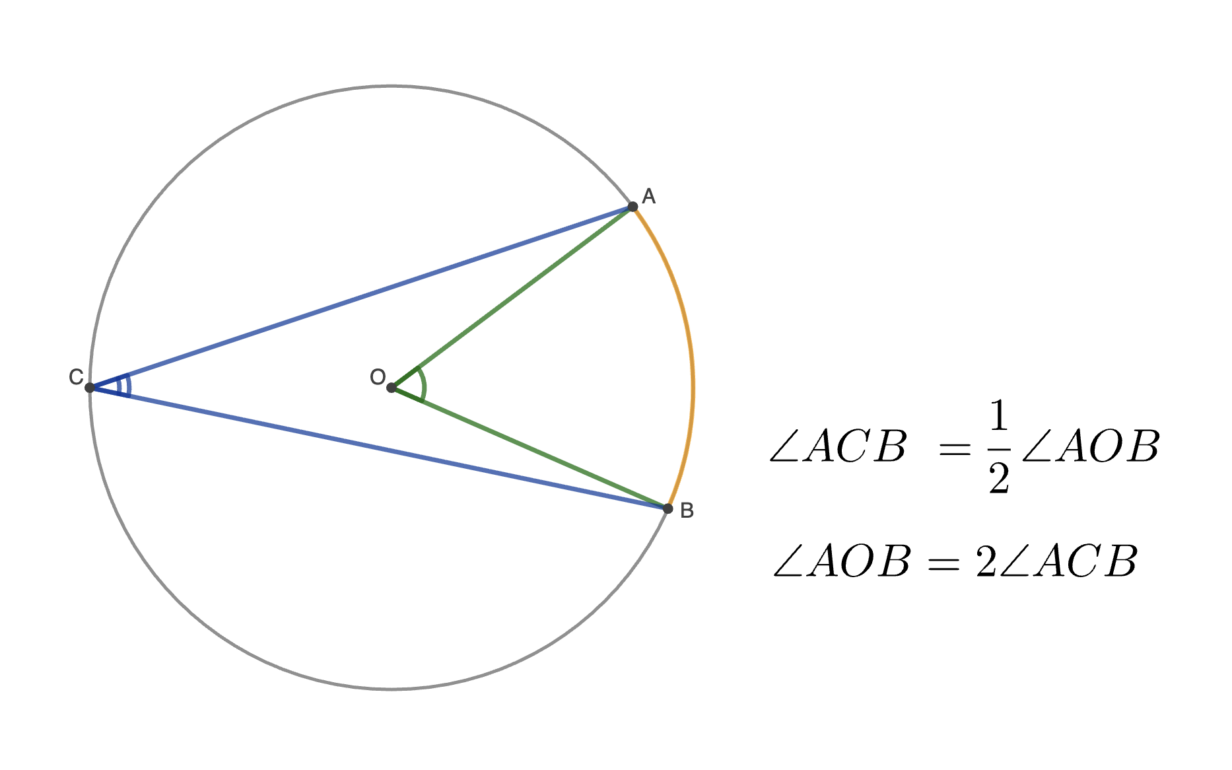
Основная теорема о вписанном угле
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, и наоборот.
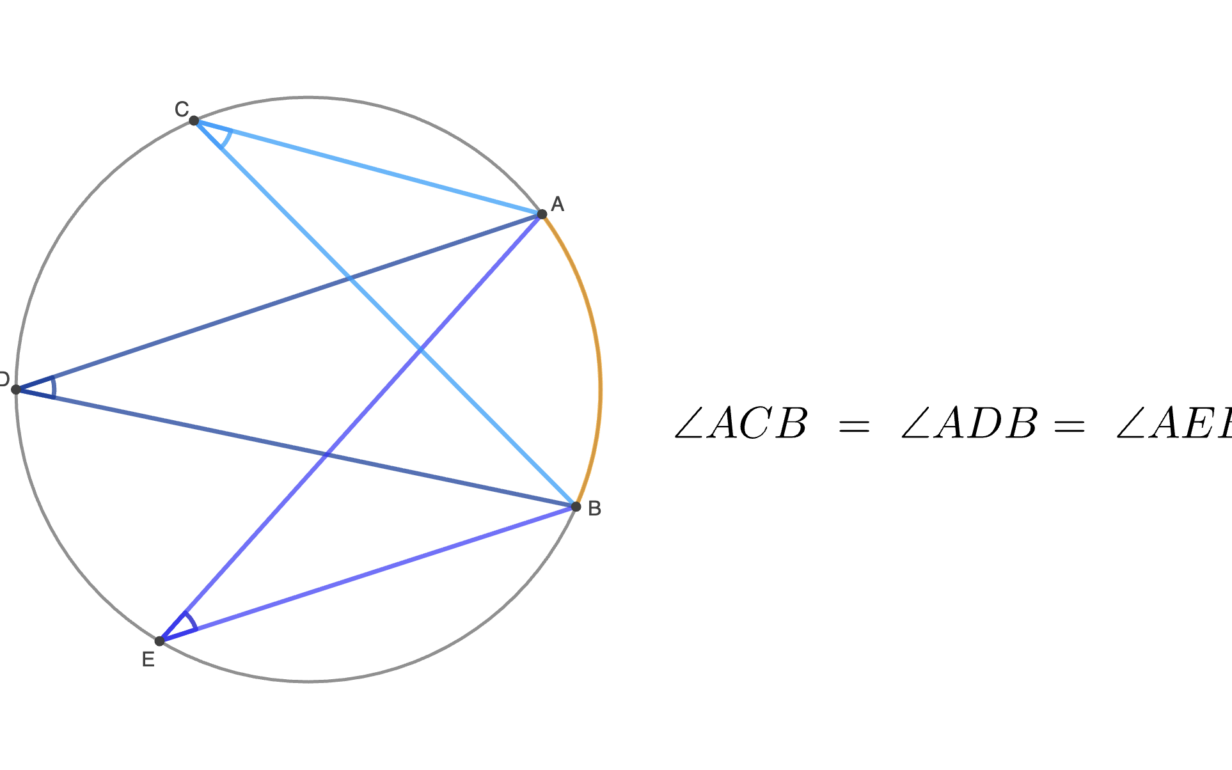
Следствие 1 из теоремы о вписанном угле
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Следствие 2 из теоремы о вписанном угле
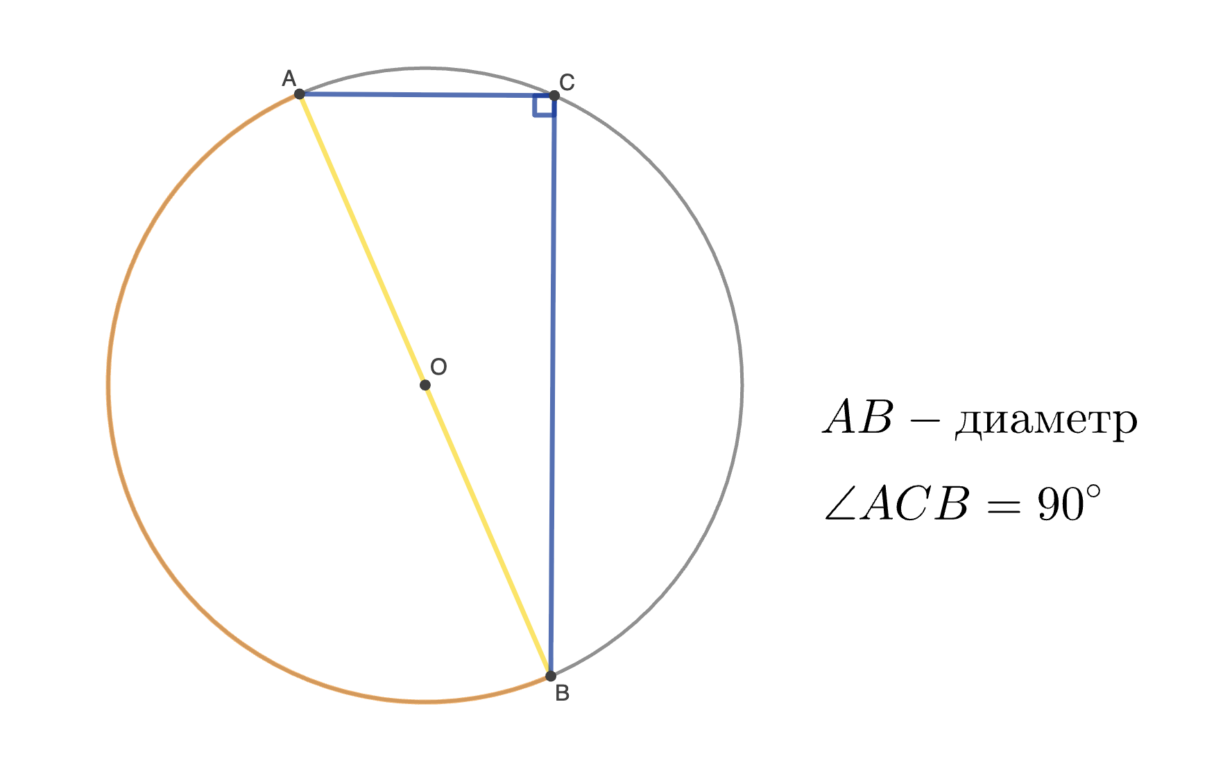
Вписанный угол, опирающийся на диаметр, прямой. И наоборот, вписанный угол, равный 90°, опирается на полуокружность.
Задачи и ответы по теме «Центральные и вписанные углы»
Теория становится по-настоящему полезной, когда применяется на практике. Решите эти задачи, чтобы закрепить понимание свойств углов в окружности и научиться видеть изученные закономерности.
Под каждой задачей представлено подробное решение — сверьтесь с ним, чтобы убедиться в правильности своих рассуждений или разобраться в допущенных ошибках
Задача 1
В окружности центральный угол AOB равен 84°. Найдите величину вписанного угла ACB, опирающегося на ту же дугу AB.
Решение и ответ к задаче 1
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу: ∠ACB = ∠AOB/2 = 84°/2 = 42°.
Ответ: 42°
Задача 2
В окружности проведен диаметр АВ. Найдите величину вписанного угла ACB, опирающегося на этот диаметр.
Решение и ответ к задаче 2
Вписанный угол, опирающийся на диаметр, всегда прямой: ∠ACB = 90°.
Ответ: 90°
Задача 3
В окружности проведены хорды AB и AC. Найдите угол ABC, если дуга AC равна 76°.
Решение и ответ к задаче 3
Угол, образованный хордами, является вписанным. Вписанный угол равен половине дуги, на которую он опирается: ∠ABC = ◡AC/2 = 76°/2 = 38°.
Ответ: 38°
Задача 4
Точки A, B, C лежат на окружности. Известно, что ∠ABC = 41°, ∠BAC = 73°. Найдите величину дуги AB.
Решение и ответ к задаче 4
Точки A, B, C образуют треугольник. Сумма углов треугольника 180°, тогда:
∠BCA = 180° — (∠ABC + ∠BAC) = 180° — (41° + 73°) = 66°
Угол BCA является вписанным, значит, дуга AB, на которую он опирается, в два раза больше: ◡AB = 2 × ∠BCA = 2 × 66° = 132°.
Ответ: 132°
Задача 5
На окружности отмечены точки A, B, C, D. Найдите угол ABD, если угол ACD равен 28°.
Решение и ответ к задаче 5
Углы ACD и ABD являются вписанными и опираются на одну дугу, а значит, они равны: ∠ABD = ∠ACD = 28°.
Ответ: 28°.
Популярные вопросы и ответы
Отвечает Андрей Маракулин, заведующий кафедрой математики и логики школы «Новый взгляд»:
Могут ли центральный и вписанный угол, опирающиеся на одну дугу, быть равны?
Центральный и вписанный углы, опирающиеся на одну дугу, не могут быть равны. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу. Это ключевая теорема о вписанном угле.
Почему тему по геометрии «Центральные и вписанные углы» изучают в 8 классе?
К этому моменту у школьников уже сформирован базовый аппарат геометрии: они знают, что такое треугольники и четырехугольники, их свойствах и формулы, связанные с ними. Эти знания необходимы для доказательства теорем, связанных с темой «Центральные и вписанные углы».
Данная тема требует понимания, аналитического мышления и построения доказательств. Это фундаментальная тема, на которой строятся более сложные и содержательные геометрические задачи.
Данная тема требует понимания, аналитического мышления и построения доказательств. Это фундаментальная тема, на которой строятся более сложные и содержательные геометрические задачи.
В каких заданиях ОГЭ и ЕГЭ по математике понадобятся знания свойств центральных и вписанных углов?
Знание свойств центральных и вписанных углов необходимо для решения заданий на вычисление углов и дуг окружности, а также в задачах, связанных с вписанными и описанными фигурами.
В ОГЭ они встречаются в задании №16 и задачах второй части: №23, №24, №25. В ЕГЭ практически любая задача по геометрии может включать в себя центральные и вписанные углы.
В ОГЭ они встречаются в задании №16 и задачах второй части: №23, №24, №25. В ЕГЭ практически любая задача по геометрии может включать в себя центральные и вписанные углы.
