Вписанная окружность
Разберемся, что такое вписанная окружность, в какие фигуры ее можно вписать, какими уникальными свойствами она обладает и как ее элементы связаны с площадью и периметром фигуры
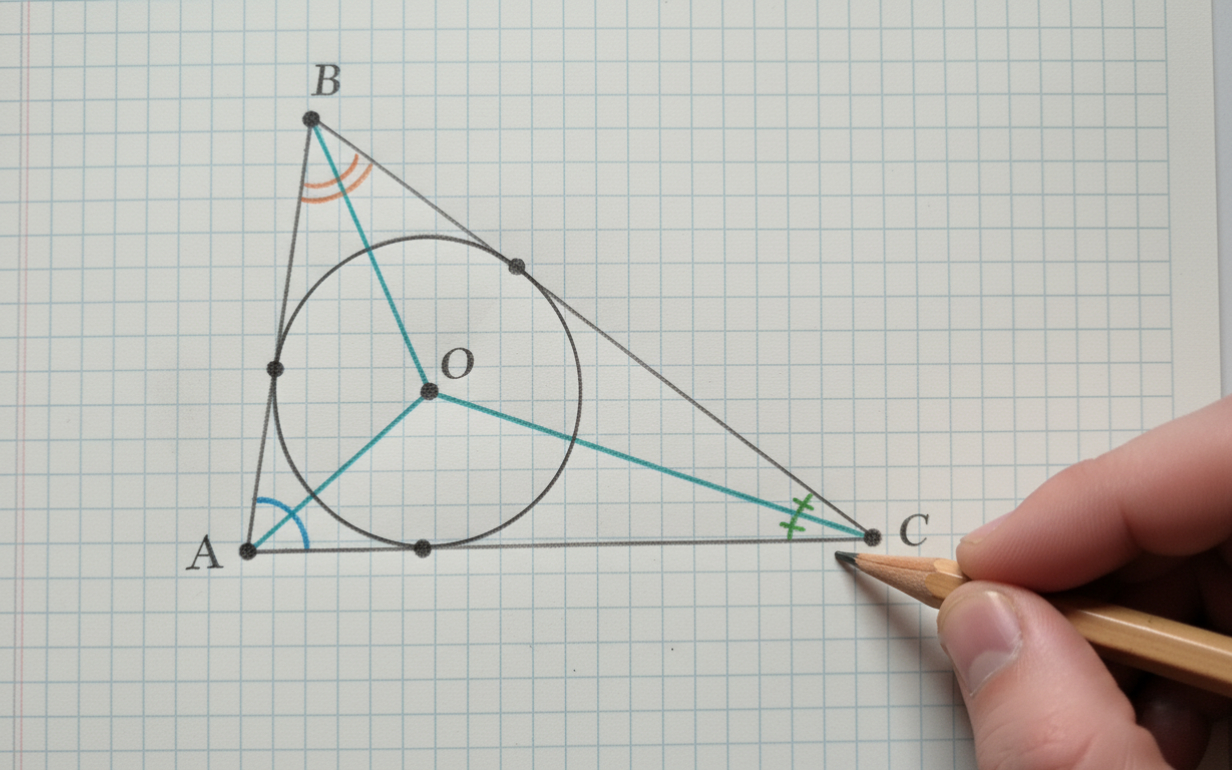
Мы уже знакомы с различными фигурами в геометрии. Некоторые из них обладают особыми свойствами, позволяющими разместить внутри окружность, которая будет касаться всех сторон. Такая окружность не просто вписана в фигуру, она находится с ней в строгом геометрическом соответствии, где положение ее центра и величина радиуса подчиняются точным законам. А называется такая окружность вписанной. Разберемся, что это, в какие фигуры ее можно вписать и какими свойствами она обладает.
Что такое вписанная окружность в геометрии
Как указано в учебнике Атанасяна Л.С. «Геометрия. 7-9 классы», входящем в Федеральный перечень учебников:1 вписанная окружность — это окружность, которая находится внутри многоугольника и касается всех его сторон. При этом стороны многоугольника являются касательными к данной окружности. Многоугольник, для которого это выполняется, называется описанным около окружности.
Центр вписанной окружности всегда равноудален от всех сторон многоугольника. Это свойство следует из самого определения окружности.
Возможность вписать окружность является не общим правилом, а особым свойством фигуры. Например, это всегда возможно для любого треугольника и правильного многоугольника, но для произвольного четырехугольника необходимо соблюдение строгих условий. Детально все эти случаи мы разберем ниже.
Полезная информация о вписанной окружности
Чтобы легко оперировать понятием вписанной окружности, важно понимать ее ключевые характеристики. Следующая таблица поможет систематизировать основные факты.
| Вписанная окружность | Описание |
|---|---|
| Центр | Точка, равноудаленная от всех сторон описанного многоугольника. |
| Радиус (r) | Перпендикуляр от центра до любой стороны многоугольника. |
| Точка касания | Точка, в которой окружность касается стороны многоугольника |
| Основное свойство | Касается всех сторон фигуры |
| Отличие от описанной окружности | Описанная окружность проходит через все вершины многоугольника, а вписанная касается всех его сторон |
Вписанная окружность в треугольник
В любой треугольник можно вписать окружность, притом только одну. Центр этой окружности, называемый инцентром, является одной из замечательных точек треугольника и всегда расположен внутри фигуры.
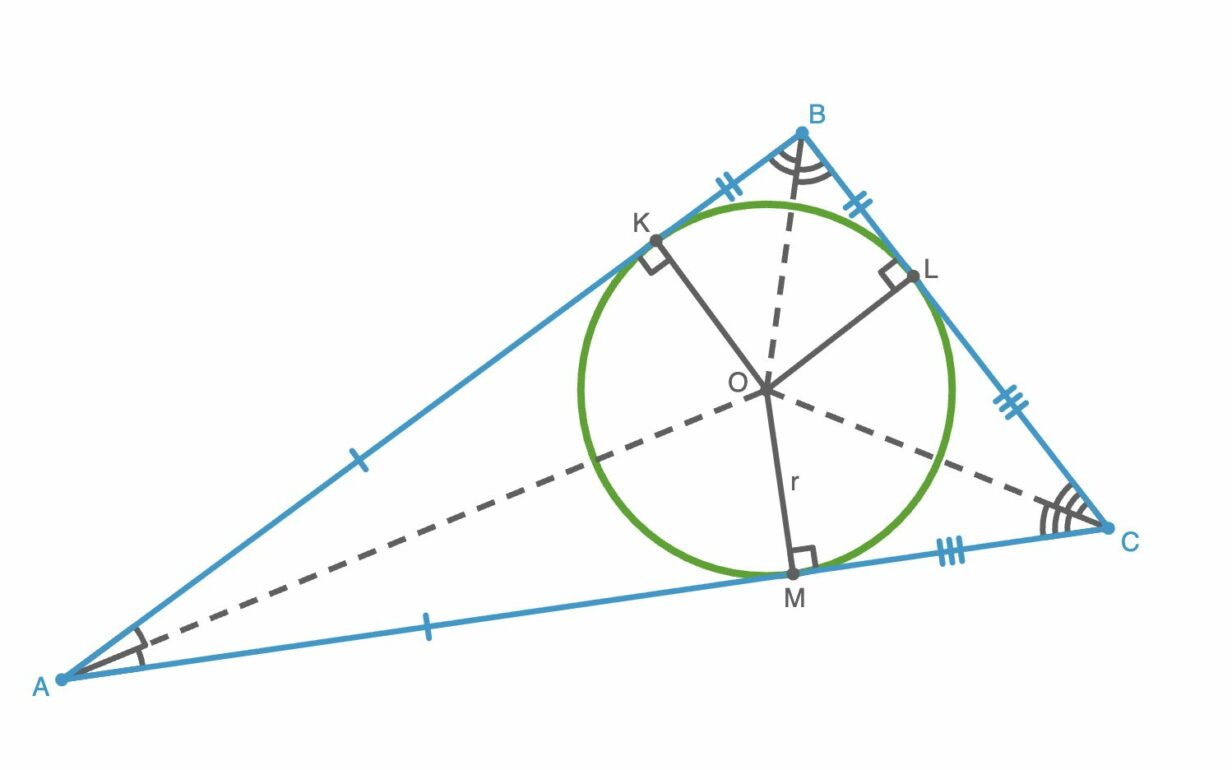
Свойства вписанной окружности в треугольник
Окружность, вписанная в треугольник, проявляется в строгих геометрических законах, которые связывают ее центр, радиус и точки касания с элементами треугольника. Эти свойства помогают не только строить окружность, но и создают удобные формулы для вычислений. Рассмотрим их.
1. Центр лежит на пересечении биссектрис треугольника. Это главное свойство, позволяющее легко построить вписанную окружность.
2. Отрезки сторон треугольника, проведенных из одной вершины к точкам касания, равны. Это свойство является прямым следствием теоремы о равенстве отрезков касательных, проведенных из одной точки к окружности.
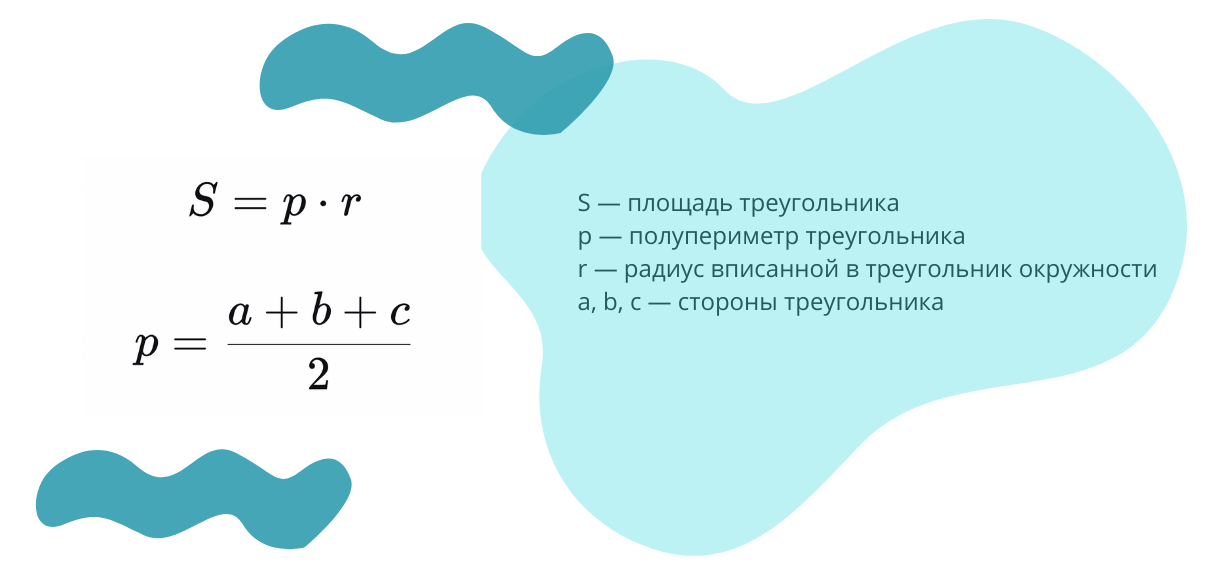
3. Площадь описанного треугольника равна произведению его полупериметра на радиус вписанной окружности:
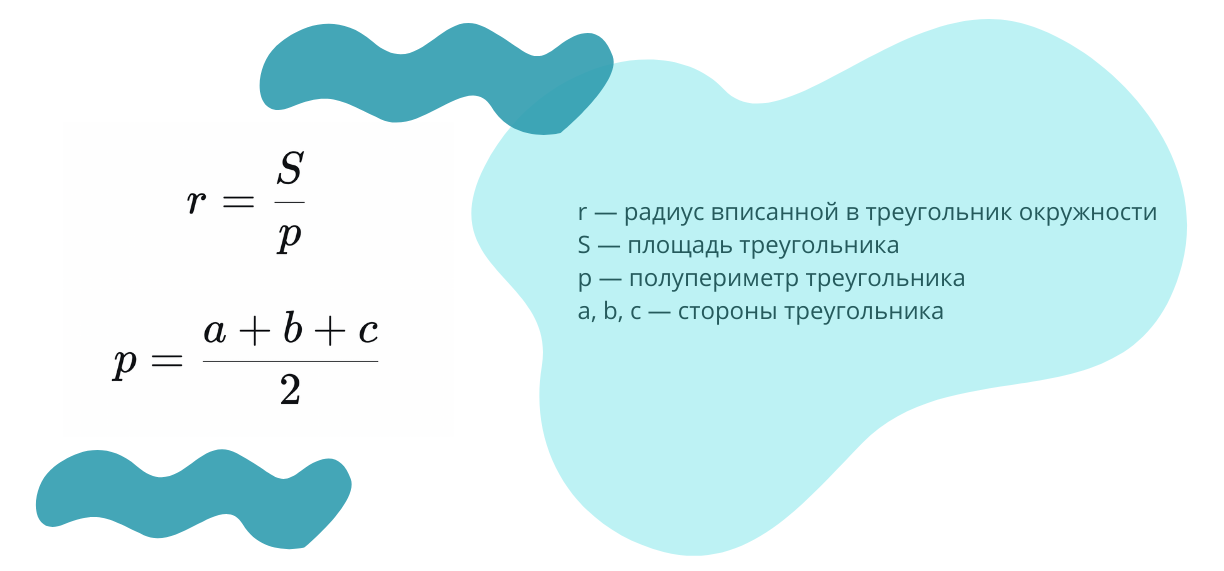
4. Радиус вписанной в треугольник окружности можно найти, поделив площадь треугольника на полупериметр:
Это прямое следствие из предыдущего свойства. Площадь треугольника при этом можно найти различными способами, используя длину сторон треугольника, высоты, радиус описанной окружности и другие.
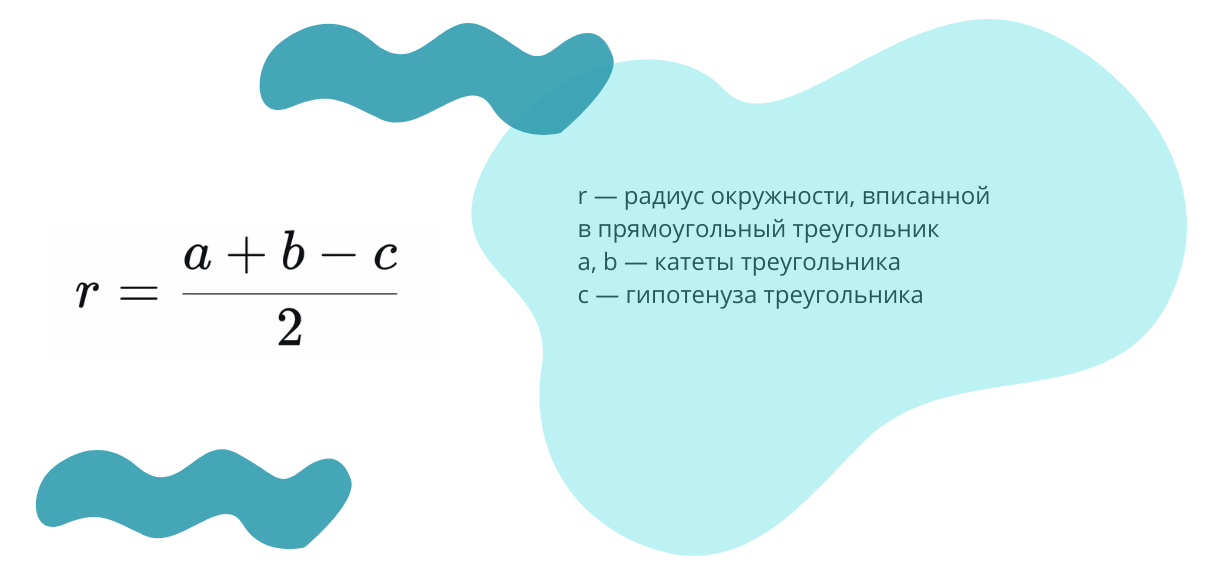
5. Радиус вписанной окружности в прямоугольный треугольник можно найти по формуле:
6. Радиус вписанной окружности в равносторонний треугольник можно найти через его сторону по формуле:
Формула Эйлера
Для любого треугольника существует удивительная связь между радиусами вписанной (r) и описанной (R) окружностей и расстоянием d между их центрами. Она выражается формулой Эйлера:
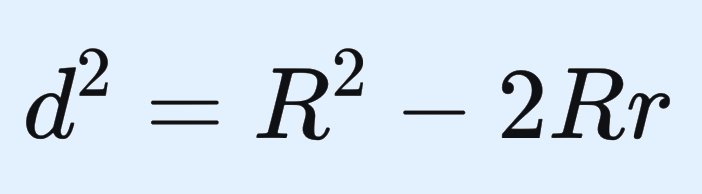
Из нее следует важное наблюдение: квадрат расстояния всегда больше нуля, а значит, радиус описанной окружности R всегда не меньше удвоенного радиуса вписанной 2r. Равенство R = 2r достигается только для правильного треугольника.
Эта формула наглядно показывает взаимное расположение двух важнейших окружностей треугольника: чем ближе расстояние между их центрами к нулю, тем ближе фигура к равносторонней.
Вписанная окружность в четырехугольник
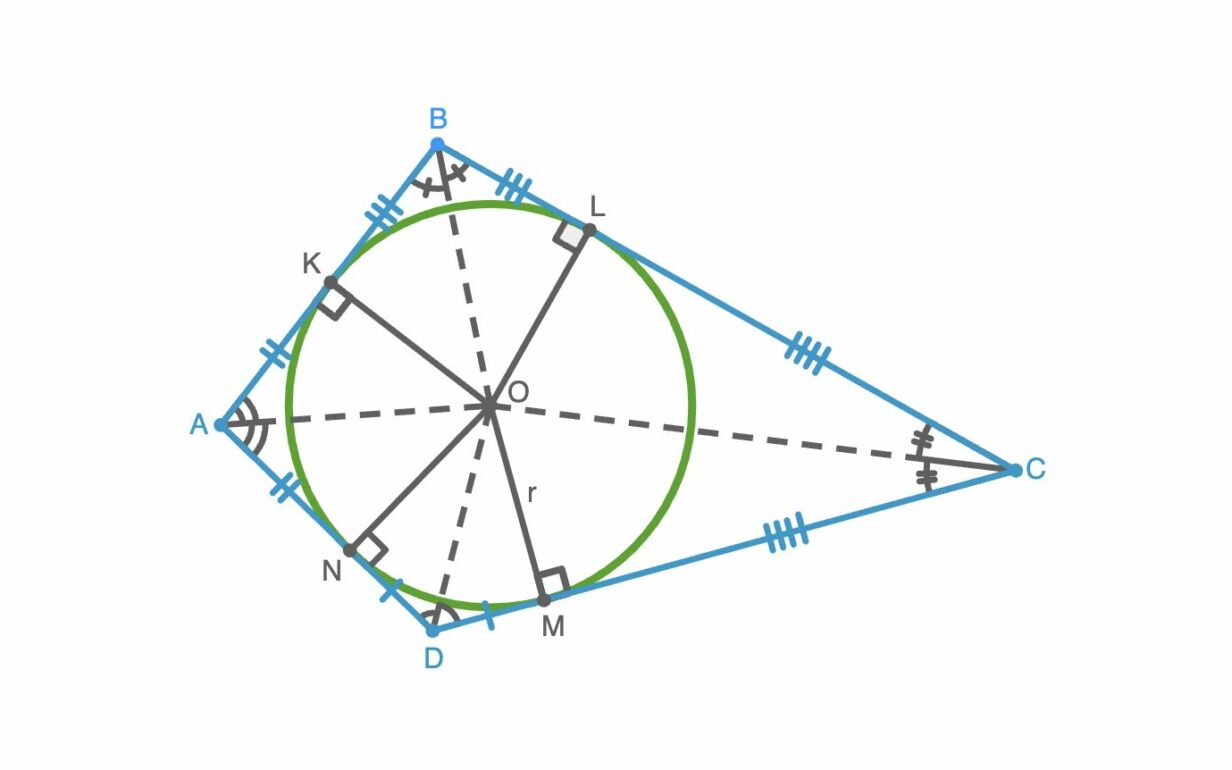
В отличие от треугольника, не в каждый четырехугольник можно вписать окружность. Для этого необходимо и достаточно выполнение определенного условия, которое называют признаком описанного четырехугольника: чтобы окружность можно было вписать в четырехугольник, суммы длин его противоположных сторон должны быть равны.
Свойства вписанной окружности в четырехугольник
Помимо ключевого признака существования, вписанная окружность наделяет четырехугольник рядом других важных характеристик. Рассмотрим их.
1. У описанного около окружности четырехугольника суммы длин противоположных сторон равны. Это основное и необходимое условие, позволяющее определить, можно ли вписать окружность в четырехугольник.
2. Центр вписанной окружности лежит на пересечении биссектрис всех углов четырехугольника.
3. Площадь описанного четырехугольника равна произведению его полупериметра на радиус вписанной окружности:
4. Радиус вписанной в четырехугольник окружности можно найти, поделив площадь четырехугольника на полупериметр:
5. Если четырехугольник является ромбом, то радиус окружности, вписанной в него, можно найти, поделив его высоту на два или заменив высоту на произведение стороны на синус угла:
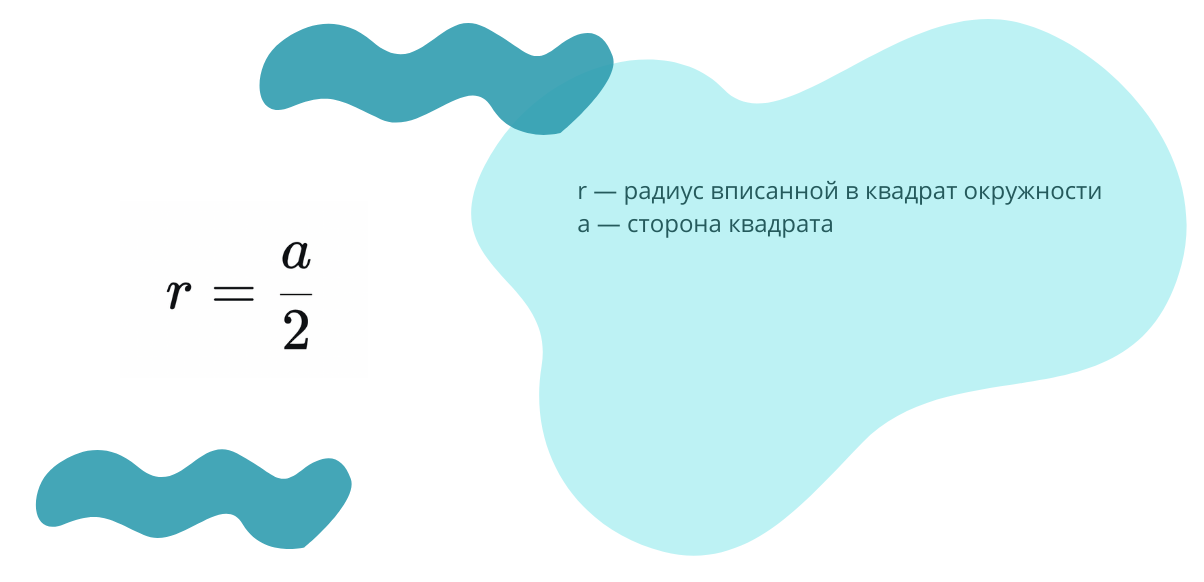
6. Если четырехугольник является квадратом, то радиус окружности, вписанной в него можно найти поделив его сторону на два:
это интересно
Вписанная окружность в многоугольник
Вписать окружность можно не только в треугольник и некоторые четырехугольники, но и в любой правильный многоугольник. Для произвольного неправильного многоугольника с количеством сторон больше четырех это возможно только при соблюдении специальных условий, связанных с равенством сумм расстояний от центра до сторон. В школьном курсе и на экзаменах подробно изучается только случай правильных многоугольников, поэтому далее мы сосредоточимся именно на них.
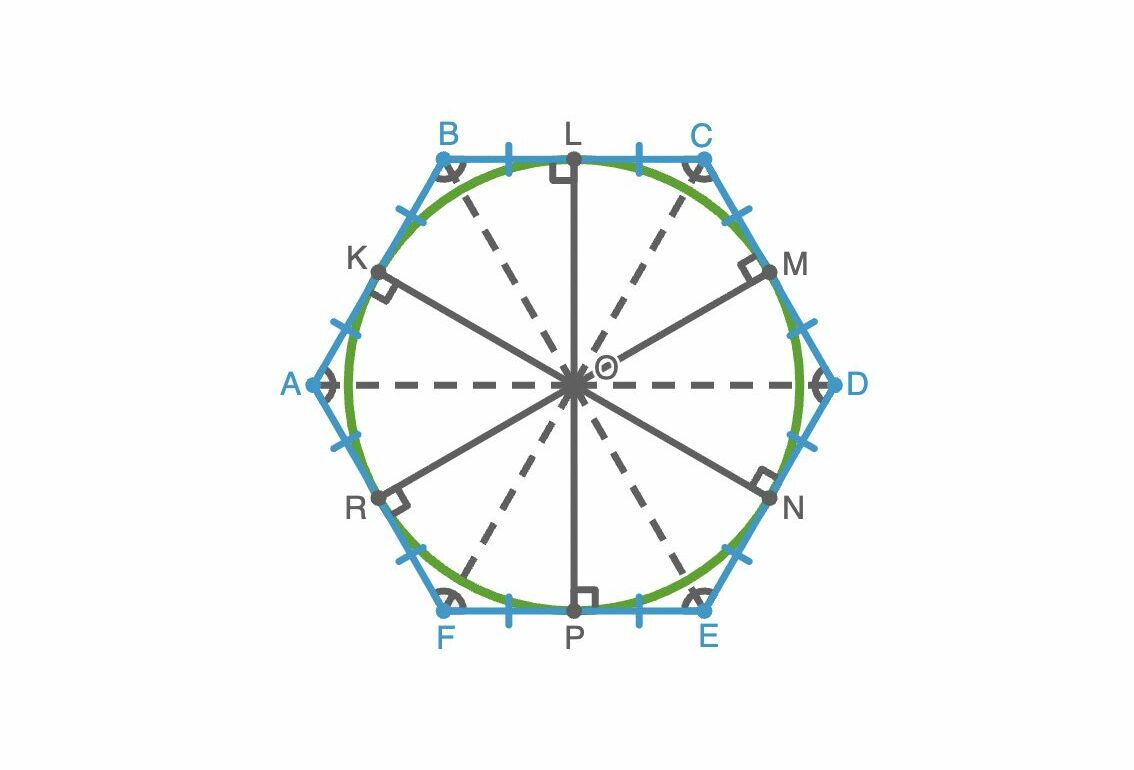
Свойства вписанной окружности в правильный n-угольник
Рассмотрим все основные свойства вписанной в правильный многоугольник окружности. В данном случае свойства проявляются в наиболее полной и симметричной форме.
1. Центр вписанной окружности совпадает с центром правильного многоугольника. Это точка, равноудаленная от всех вершин и всех сторон правильного многоугольника.
2. Каждая сторона правильного многоугольника касается окружности в своей середине.
3. Площадь описанного правильного многоугольника равна произведению его полупериметра на радиус вписанной окружности:
4. Радиус вписанной окружности в правильный многоугольник можно найти, разделив площадь многоугольника на его полупериметр:
5. Радиус вписанной окружности в правильный многоугольник можно найти через его сторону по формуле:
6. Радиус вписанной окружности в правильный многоугольник можно найти через радиус описанной окружности по формуле:
Эти формулы выводятся из рассмотрения прямоугольного треугольника, образованного радиусом вписанной окружности (апофемой), половиной стороны многоугольника и радиусом описанной окружности.
Задачи и ответы по теме «Вписанная окружность»
Решение задач помогает не только закрепить формулы, но и увидеть, как свойства вписанной окружности связывают воедино элементы описанной фигуры. Попробуйте решить задачи разного уровня сложности, чтобы уверенно применять изученные законы.
Задача 1
В треугольнике ABC известно, что AB = 13 см, BC = 14 см, AC = 15 см. Найдите радиус окружности, вписанной в этот треугольник.
Решение и ответ к задаче 1
Найдем полупериметр треугольника:
p = (AB + BC + AC) / 2
p = (13 + 14 + 15) / 2 = 21 (см)
Найдем площадь треугольника по формуле Герона:
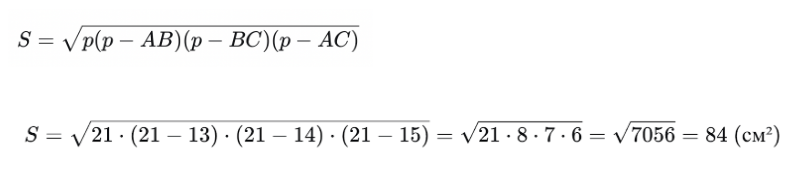
Найдем радиус окружности, вписанной в треугольник по формуле:
r = S / p
r = 84 / 21 = 4 (см)
Ответ: 4 см
Задача 2
Стороны выпуклого четырехугольника, взятые последовательно, равны 7 см, 8 см, 9 см и 10 см. Можно ли в этот четырехугольник вписать окружность? Ответ обоснуйте.
Решение и ответ к задаче 2
Чтобы окружность можно было вписать в четырехугольник, суммы противоложных сторон этого четырехугольника должны быть равны.
Проверяем:
7 + 9 = 16 (см)
8 + 10 = 18 (см)
16 см ≠ 18 см
Условие не выполняется.
Ответ: нет, в такой четырехугольник нельзя вписать окружность
Задача 3
Найдите сторону квадрата, если радиус вписанной в него окружности равен 5√2 см.
Решение и ответ к задаче 3
Для квадрата радиус вписанной окружности равен половине стороны:
r = a / 2
Следовательно, сторона квадрата вычисляется по формуле:
a = 2r
a = 2 × 5√2 = 10√2 (см)
Ответ: 10√2 см
Задача 4
Периметр правильного шестиугольника равен 72 см. Найдите радиус вписанной в него окружности.
Решение и ответ к задаче 4
Периметр правильного шестиугольника вычисляется по формуле:
P = 6a
Тогда сторону можно найти разделив периметр на 6:
a = P / 6
a = 72 / 6 = 12 (см)
Радиус вписанной окружности находим по формуле:
r = a / 2tg(180°/n)
r = 12 / 2tg(180°/6) = 12 / (2 × (√3/3)) = 6√3 (см)
Ответ: 6√3 см
Решение данных задач на вписанную окружность соответствует требованиям Федеральной рабочей программы по математике2 и проверяется на государственной итоговой аттестации.
Популярные вопросы и ответы
Отвечает Михаил Ушаков, преподаватель математики онлайн-школы ЕГЭLand:
Как найти радиус окружности, вписанной в прямоугольный треугольник, если известны только его катеты?
Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле: r = (a + b – c) / 2, где a и b — катеты, c — гипотенуза. Если же нужно использовать только катеты, гипотенузу выражают через теорему Пифагора, где она равняется квадратному корню из суммы квадратов катетов. Формула получается длиннее, но позволяет обойтись без дополнительных данных.
Как меняется радиус вписанной окружности, если все стороны треугольника увеличить в два раза?
При увеличении всех сторон в 2 раза треугольник остается подобным исходному. Коэффициент подобия (k = 2) влияет на все линейные размеры. Площадь при этом увеличится в четыре раза, а полупериметр — в два. Поскольку радиус вписанной окружности находится по формуле r = S / p, он также увеличится в два раза (4/2 = 1). Эта закономерность сохраняется для любых подобных фигур.
Почему нельзя вписать окружность в прямоугольник, если он не является квадратом?
Чтобы окружность считалась вписанной, она должна касаться всех сторон четырехугольника. Это возможно только тогда, когда суммы противоположных сторон равны.
У прямоугольника это выполняется лишь в одном случае — когда он квадрат. Если стороны разные, окружность коснется максимум трех сторон и уже не будет вписанной.
У прямоугольника это выполняется лишь в одном случае — когда он квадрат. Если стороны разные, окружность коснется максимум трех сторон и уже не будет вписанной.
Что такое вневписанная окружность треугольника?
Вневписанная окружность касается одной стороны треугольника и продолжений двух других. Таких окружностей у треугольника три.
Любопытный факт: если окружность касается стороны AC треугольника ABC, то отрезок BM, где M — точка касания продолжения стороны BA с окружностью, равен полупериметру треугольника. А точки касания вписанной и вневписанной окружностей со стороной симметричны относительно ее середины.
Любопытный факт: если окружность касается стороны AC треугольника ABC, то отрезок BM, где M — точка касания продолжения стороны BA с окружностью, равен полупериметру треугольника. А точки касания вписанной и вневписанной окружностей со стороной симметричны относительно ее середины.
Почему тему по геометрии «Вписанная окружность» изучают в 8 классе?
Эта тема входит в базовый курс планиметрии 7–9 классов. В 7 классе ученики знакомятся с самим понятием вписанной и описанной окружностей. В 8 классе, после изучения признаков равенства треугольников, свойств биссектрисы и основных теорем, школьники уже имеют достаточную базу для глубокого анализа: доказательства свойств, вывода формул для радиуса и решения прикладных задач.
В каких заданиях ОГЭ и ЕГЭ встречаются задачи на вписанную окружность?
На ОГЭ подобные задачи чаще всего попадаются в номере 16 первой части и номерах 23, 24, 25 второй части, где нужно оформить полное решение. В ЕГЭ базового уровня по математике знания свойств вписанной окружности может понадобиться для решения следующих заданий: №8, №10, №12. На ЕГЭ по профильной математике элементы этой темы могут встретиться в заданиях №1, №14, №17.
Структура КИМ (контрольных измерительных материалов) и распределение тем по заданиям периодически корректируются Федеральным институтом педагогических измерений (ФИПИ)3. Поэтому выпускникам и педагогам каждый учебный год необходимо обращаться к актуальным спецификациям, кодификаторам и демонстрационным вариантам на официальном сайте ФИПИ, чтобы отслеживать возможные изменения.
Таким образом, главная задача ученика — не заучивать номера заданий, а глубоко понимать свойства вписанной окружности, формулы и принципы их применения. Владея теорией, вы сможете распознать и решить соответствующую задачу в любом формате и под любым номером в экзаменационной работе.
Структура КИМ (контрольных измерительных материалов) и распределение тем по заданиям периодически корректируются Федеральным институтом педагогических измерений (ФИПИ)3. Поэтому выпускникам и педагогам каждый учебный год необходимо обращаться к актуальным спецификациям, кодификаторам и демонстрационным вариантам на официальном сайте ФИПИ, чтобы отслеживать возможные изменения.
Таким образом, главная задача ученика — не заучивать номера заданий, а глубоко понимать свойства вписанной окружности, формулы и принципы их применения. Владея теорией, вы сможете распознать и решить соответствующую задачу в любом формате и под любым номером в экзаменационной работе.
Источники
Материал подготовлен на основании официальных документов и рекомендаций:
1. Министерство просвещения России. Федеральный перечень учебников. URL: https://fpu.edu.ru/
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. «Геометрия. 7-9 классы. Базовый уровень»
- Смирнов В.А., Смирнова И.М. «Геометрия. 7 класс»
- Смирнов В.А., Смирнова И.М. «Геометрия. 8 класс»
- Смирнов В.А., Смирнова И.М. «Геометрия. 9 класс»
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. «Геометрия. 10-11 классы. Базовый и углубленный уровни»
- Мерзляк А.Г., Номировский Д.А., Поляков В.М. «Геометрия. 10 класс. Углубленный уровень»
- Мерзляк А.Г., Номировский Д.А., Поляков В.М. «Геометрия. 11 класс. Углубленный уровень»
2. Министерство просвещения России. Федеральная рабочая программа по учебному предмету «Математика». URL: https://static.edsoo.ru/projects/fop/index.html#/sections/200215
3. Федеральный институт педагогических измерений. Открытый банк заданий ОГЭ и ЕГЭ по математике. Методические рекомендации для учителей. URL: https://fipi.ru/
