Высота треугольника: что такое, формулы, свойства, задачи с ответами по геометрии для 7 класса и подготовки к ЕГЭ по математике, геометрии

Одна из фундаментальных фигур геометрии — треугольник, а его свойства находят применение в различных областях науки и техники. Одним из ключевых элементов треугольника является высота, которая не только связана с вычислением площади, но и играет важную роль в геометрических построениях и доказательствах теорем.

Что такое высота треугольника в геометрии

Высота треугольника — это перпендикуляр, опущенный из любой вершины треугольника на прямую, содержащую противоположную сторону.

Высота треугольника. Изображение: Ирина Соколова

Важно понимать, что высота всегда образует прямой угол с основанием. Это ключевое свойство отличает высоту от других элементов треугольника, таких как медиана и биссектриса.

Каждый треугольник имеет три высоты, по одной из каждой вершины. Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром. Расположение ортоцентра зависит от типа треугольника и может находиться внутри фигуры, на ее границе или вне треугольника.

Полезная информация о высоте треугольника

Высота треугольника обладает рядом важных геометрических свойств. В таблице собраны основные характеристики, позволяющие быстро вспомнить наиболее важные факты о высотах треугольника, которые пригодятся при изучении геометрии и решении практических задач.

Высота треугольника	Описание
Количество высот	В любом треугольнике ровно три высоты, по одной из каждой вершины
Геометрические свойства	Всегда образует прямой угол с основанием. Может лежать внутри и вне треугольника. Наименьшая сторона соответствует наибольшей стороне
Ортоцентр	Точка пересечения высот. Может находиться внутри, на стороне или вне треугольника
Связь с площадью	Основная формула: h = 2S/a, где h – высота, S – площадь, a – сторона, к которой проведена высота

Высота в остроугольном треугольнике

В остроугольном треугольнике все углы меньше 90°, поэтому все три высоты проходят внутри треугольника. Каждая высота опускается на сторону треугольника, не пересекая ее продолжение.

Ортоцентр остроугольного треугольника располагается внутри фигуры. Это единственный тип треугольника, где точка пересечения высот находится внутри самого треугольника.

Высоты в остроугольном треугольнике. Изображение: Ирина Соколова

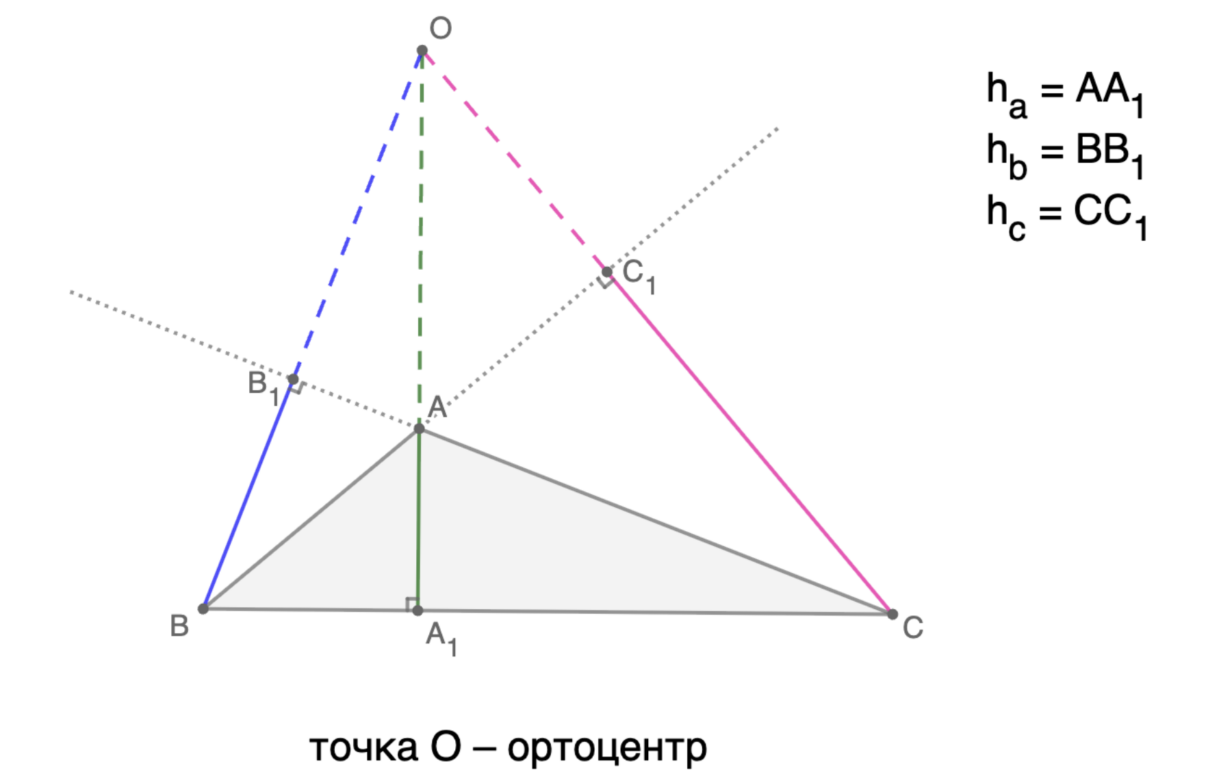
Возьмем остроугольный треугольник ABC. Из вершины A опустим перпендикуляр на сторону BC — это будет высота h_a. Аналогично строим высоты h_b и h_c из вершин B и C соответственно. Все три высоты пересекаются в точке O внутри треугольника.

Высота в тупоугольном треугольнике

В тупоугольном треугольнике один угол больше 90°. Высота, опущенная из вершины тупого угла, проходит внутри треугольника, а две другие высоты опускаются на продолжения сторон и проходят вне треугольника.

Ортоцентр тупоугольного треугольника находится за пределами фигуры, со стороны, противоположной тупому углу.

Высоты в тупоугольном треугольнике. Изображение: Ирина Соколова

В треугольнике ABC с тупым углом при вершине A высота h_a опускается на сторону BC внутри треугольника. Высоты h_b и h_c опускаются на продолжения сторон AC и AB соответственно, проходя вне треугольника.

Высота в прямоугольном треугольнике

Прямоугольный треугольник имеет особые свойства относительно высот. Две высоты совпадают с катетами треугольника, а третья высота опускается из вершины прямого угла на гипотенузу.

Ортоцентр прямоугольного треугольника находится в вершине прямого угла. Это объясняется тем, что катеты перпендикулярны друг другу и являются высотами треугольника.

Высоты в прямоугольном треугольнике. Изображение: Ирина Соколова

В треугольнике ABC с прямым углом при вершине C высота h_с опускается на гипотенузу AB внутри треугольника. Высоты h_a и h_b совпадают с катетами AC и BC соответственно.

Высота, проведенная к гипотенузе, обладает важными свойствами:

делит прямоугольный треугольник на два треугольника, подобных исходному;
равна произведению катетов, деленному на гипотенузу;
равна среднему геометрическому проекций катетов на гипотенузу.

Свойство высоты, проведенной к гипотенузе. Подобие треугольников. Изображение: Ирина Соколова

Свойство высоты, проведенной к гипотенузе. Нахождение высоты через катеты и гипотенузу. Изображение: Ирина Соколова

Свойство высоты, проведенной к гипотенузе. Нахождение высоты через проекции катетов на гипотенузу. Изображение: Ирина Соколова

Формулы нахождения высоты в треугольнике

Высоту треугольника можно вычислить различными способами в зависимости от известных параметров. Рассмотрим основные формулы.

Через площадь и длину стороны, к которой опущена высота

Это основная и наиболее часто используемая формула для нахождения высоты треугольника:

\(\mathrm h\;=\frac{2\mathrm S}{\mathrm a},\;\mathrm{где}:\;\)

h — высота, проведенная к стороне a;
S — площадь треугольника;
a — длина стороны, к которой проведена высота.

Данная формула работает для треугольников любого типа.

Эта фундаментальная формула является основой для всех остальных способов вычисления высоты. Если значение площади неизвестно, то ее можно выразить через значения других параметров треугольника.

Через другую высоту и стороны, к которым проведены высоты

Если известна одна высота треугольника и требуется найти другую, можно использовать соотношение:

\({\mathrm h}_{\mathrm a}\;\;=\;\frac{{\mathrm{bh}}_{\mathrm b}}{\mathrm a},\;\mathrm{где}:\;\)

h_a – высота, проведенная к стороне a;
h_b – высота, проведенная к стороне b;
a – длина стороны, к которой проведена высота h_a;
b – длина стороны, к которой проведена высота h_b.

Это соотношение следует из формулы площади (S = ½ ah_a = ½ bh_b) и позволяет выразить одну высоту через другую.

Через длины всех сторон треугольника

Когда известны все три стороны треугольника, высоту можно найти, используя формулу Герона:

\(\mathrm h\;=\;\frac{2\sqrt{\mathrm p(\mathrm p-\mathrm a)(\mathrm p-\mathrm b)(\mathrm p-\mathrm c)}}{\mathrm a},\;\mathrm{где}:\)

h — высота, проведенная к стороне a;
p = a+b+c / 2 — полупериметр треугольника;
a, b, c — длины сторон треугольника.

С помощью формулы Герона мы находим площадь, а затем применяем основную формулу h = 2S/a.

это интересно

Средняя линия треугольника

Что такое средняя линия треугольника и для чего она нужна

Подробнее

Через сторону и прилежащий угол

Если известна сторона треугольника и прилежащий к ней угол, высоту можно найти с помощью тригонометрической функции:

h_a = b × sinC, где:

h_a — высота, проведенная к стороне a
b — другая сторона треугольника
sinC — угол между сторонами a и b.

Данное формула выводится из тригонометрического выражения площади S = ½ absinC, которое подставляется в основную формулу h = 2S/a.

В прямоугольном треугольнике

Для прямоугольного треугольника существуют специальные формулы нахождения высоты:

\(\mathrm h\;=\;\frac{\mathrm{ab}}{\mathrm с},\;\mathrm{где}:\)

h — высота, проведенная к гипотенузе
a, b — катеты;
c — гипотенуза.

\(\mathrm h\;=\;\sqrt{{\mathrm c}_{\mathrm a}{\mathrm c}_{\mathrm b}},\;\mathrm{где}:\)

h — высота, проведенная к гипотенузе;
c_a — проекция катета a на гипотенузу;
c_b – проекция катета b на гипотенузу.

Эти формулы являются следствием свойств подобных треугольников и теоремы Пифагора.

В равнобедренном треугольнике

Для равнобедренного треугольника можно вывести дополнительную формулу нахождения высоты:

\(\mathrm h\;=\;\sqrt{\mathrm a^2-\frac{\mathrm b^2}4},\;\mathrm{где}:\)

h — высота, опущенная к основанию;
a — длина боковой стороны;
b — длина основания.

Формула следует из теоремы Пифагора, примененной к прямоугольному треугольнику, образованному высотой, боковой стороной и половиной основания.

В равностороннем треугольнике

Для равностороннего треугольника все высоты равны и вычисляются по формуле:

\(\mathrm h\;=\;\frac{\mathrm a\sqrt3}2,\;\mathrm{где}:\)

h — любая из трех равных высот треугольника;
a — длина стороны треугольника.

Формула является частным случаем формулы для равнобедренного треугольника, где все стороны равны.

Свойства высоты треугольника

Высоты треугольника обладают рядом уникальных характеристик, которые широко применяются в геометрических задачах.

Перпендикулярность
Высота всегда перпендикулярна стороне, на которую опущена.
Пересечение в одной точке
Все три высоты треугольника пересекаются в одной точке — ортоцентре.
Наименьшая и наибольшая высота
В любом треугольнике наименьшая высота опущена на наибольшую сторону и наоборот.
Связь с медианой и биссектрисой
В равнобедренном треугольнике высота, опущенная на основание, является также медианой и биссектрисой.
Деление на подобные треугольники
Высота, опущенная на гипотенузу прямоугольного треугольника, делит его на два подобных исходному треугольника.

Задачи на тему «Высота треугольника»

Мы разобрали основные свойства и формулы, связанные с высотой треугольника, — пришло время применить эти знания на практике.

Задача 1

В треугольнике ABC площадь равна 36 см², сторона AB = 9 см. Найдите высоту, опущенную на сторону AB.

Задача 2

У треугольника со сторонами 2 м и 10 м проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 5 м. Чему равна высота, проведенная ко второй стороне?

Задача 3

Стороны треугольника равны 5 см, 12 см и 13 см. Найдите высоту, опущенную на сторону длиной 13 см.

Задача 4

В равнобедренном треугольнике основание равно 16 см, а боковая сторона – 10 см. Найдите высоту, опущенную на основание.

Ответы к задачам

Проверьте, правильно ли вы выполнили задания. Ниже приведены подробные решения с ответами.

Задача 1

Используем формулу связи площади и высоты:

\(\mathrm h\;=\;\frac{2\mathrm S}{\mathrm a}\;=2\times\frac{36}9\;=\;8\;\mathrm{см}\)

Ответ: 8 см

Задача 2

Нам известно, что найти площадь треугольника мы можем с помощью формулы S = ¹/₂ ah_a или S = ¹/₂ bh_b

Тогда ah_a = bh_b

Выразим искомую высоту

\({\mathrm h}_{\mathrm b}\;=\;\frac{{\mathrm{ah}}_{\mathrm a}}{\mathrm b}\;=\;2\;\times\;\frac5{10}\;=\;1\mathrm м\)

Ответ: 1 м

Задача 3

Проверяем тип треугольника:

5² + 12²= 25 + 144 = 169 = 13²

Сумма квадратов длин двух сторон равна квадрату длины третьей, значит, треугольник прямоугольный. Соответственно, стороны с длинами 5 см и 12 см являются катетами, а гипотенуза равна 13 см.

Найдем длину высоты, проведенной к гипотенузе, по формуле:

\(\mathrm h=\frac{\mathrm{ab}}{\mathrm c}\;=\;5\;\times\frac{12}{13}\;=\frac{60}{13}\mathrm{см}\;\approx4,5\;\mathrm{см}\)

Ответ: ⁶⁰/₁₃ см

Задача 4

Высота, проведенная к основанию, боковая сторона и половина основания образуют прямоугольный треугольник. Соответственно, мы можем рассчитать высоту с помощью теоремы Пифагора.

Половина основания равна 16 : 2 = 8 см

Тогда:

\(\mathrm h\;=\;\sqrt{10^2-\;8^2}\;=\;\sqrt{36}\;=\;6\mathrm{см}\)

Ответ: 6 см

Популярные вопросы и ответы

Отвечает Ольга Комарова, учитель математики:

Что такое высота, проведенная к гипотенузе?

Давайте вспомним определение: высота треугольника — это перпендикуляр, который проведен из вершины треугольника к прямой, содержащей противоположную сторону.

В прямоугольном треугольнике одна из самых интересных высот — та, что опускается на гипотенузу из вершины прямого угла. Она разбивает треугольник на два новых, и все три оказываются подобными друг другу — это основа для многих задач на нахождение отрезков, построение отношений, работу с пропорциями.

При этом важно понимать, что в прямоугольном треугольнике две стороны, образующие прямой угол, уже являются высотами. И это часто вводит школьников в заблуждение, особенно в задачах, где нужно построить все три высоты. Кажется, что ничего не дано, а на самом деле две высоты уже есть — это стороны треугольника.

А еще высота — пожалуй, единственный элемент треугольника, который может выходить за его пределы. Например, в тупоугольном треугольнике высоту приходится опускать на продолжение стороны. Такие задачи в геометрии учат важному: что иногда надо мыслить за пределами фигуры — буквально.

Почему тему по геометрии «Высота треугольника» изучают в 7 классе?

К этому моменту у школьников уже достаточно геометрического опыта. Ученики умеют строить треугольники, знают свойства углов, могут работать с прямыми и так далее. А значит, готовы изучить что может находится внутри фигур. Высота — это и перпендикуляр, и средство вычисления площади, и начало логических построений. Через нее удобно формулировать и доказывать свойства, применять теорему Пифагора, изучать подобие фигур.

Именно в 7 классе закладывается важный навык — видеть в чертеже больше, чем просто линии. Понимать, что каждая из них может быть не просто стороной, а одновременно и высотой, и медианой, и элементом рассуждения.

В каком задании ЕГЭ по математике может понадобиться знание темы «Высота в треугольнике»?

Знание темы «Высота в треугольнике» может понадобиться практически в любом задании ЕГЭ, где есть геометрия, базовый ли уровень или профильный. Это задачи на площади, нахождение длин, построение перпендикуляров, деление треугольников. В задачах на доказательство часто опираются на свойства высоты: как перпендикуляра, как линии, проходящей через ортоцентр, или как ключевого элемента построения. В базовой части — в задачах на нахождение площади и работы с формулами.
По сути, умение работать с высотой — это один из базовых геометрических инструментов для решения задач.