Дифракция света
Замечали ли вы, как в полутьме уличные фонари окутаны мягким сиянием? Этот красивый оптический эффект — проявление дифракции света. Расскажем, что это такое

Вы наверняка видели, как солнечный свет, проходя через полуприкрытые жалюзи, создает на стене причудливые полосы или как радужные переливы появляются на поверхности компакт-диска. Эти удивительные явления объясняются дифракцией света — фундаментальным свойством волновой природы света, которое мы наблюдаем чаще, чем кажется. В этой статье мы разберемся, почему свет способен огибать препятствия, как это свойство используют в современных технологиях и где можно наблюдать дифракцию в повседневной жизни.
Что такое дифракция света в физике
Дифракция света — это физическое явление, при котором световая волна, встречая на своем пути препятствие или проходя через отверстие малых размеров, отклоняется от первоначального направления распространения.
Это фундаментальное проявление волновой природы света, наблюдаемое в случаях, когда размеры препятствий или отверстий оказываются сравнимы с длиной световой волны. В отличие от простого преломления или отражения, дифракция приводит к сложному перераспределению световой энергии в пространстве, создавая характерные картины распределения интенсивности с чередующимися светлыми и темными областями.
Дифракционные эффекты играют важную роль как в природных оптических явлениях, так и в современных технологиях, начиная от простых оптических приборов и заканчивая сложными научными установками.
Полезная информация о дифракции света
Дифракция света проявляется в различных физических явлениях и технических устройствах. Для лучшего понимания этого явления полезно знать его ключевые характеристики и параметры. В таблице ниже собраны основные сведения о дифракции, которые помогут систематизировать знания.
| Характеристика дифракции света | Описание |
|---|---|
| Условие четкого наблюдения | Размер препятствия ≈ λ (400–700 нм для видимого света) |
| Ключевой принцип | Принцип Гюйгенса-Френеля (огибание препятствий вторичными волнами) |
| Закон для дифракционной решетки | dsinθ = mλ (где d — период решетки, m — порядок спектра, θ — угол наблюдения, λ — длина световой волны) |
| Характерные картины | Чередующиеся светлые и темные полосы (на щели) или радужные спектры (на решетке) |
Условия возникновения дифракции света
Дифракция света проявляется не всегда, а только при соблюдении определенных условий. Главное требование — размер препятствия или отверстия должен быть сопоставим с длиной волны света. Для видимого света (400-700 нм) это означает, что мы сможем наблюдать четкую дифракционную картину, когда препятствие имеет размер порядка микрона — например, тонкая щель шириной 0,01-0,1 мм или человеческий волос.
Важную роль играет характер световой волны. Наиболее четкие дифракционные картины получаются с когерентным излучением, где все волны согласованы по фазе. Именно поэтому лазерный луч идеально подходит для демонстрации дифракции — его когерентность позволяет наблюдать устойчивые интерференционные полосы. Обычные источники света, такие как лампочки, требуют дополнительной фильтрации для выделения узкого спектрального диапазона.
Расстояние от препятствия до экрана наблюдения также влияет на результат. В так называемой зоне Фраунгофера (достаточно далеко от препятствия) дифракционная картина становится наиболее четкой и устойчивой. На практике для наблюдения в школьной лаборатории обычно достаточно расстояния 1-2 метра. При этом важно помнить, что дифракция — это универсальное волновое явление, и аналогичные эффекты можно наблюдать не только со светом, но и с звуковыми волнами или волнами на воде.

Принцип Гюйгенса-Френеля
Этот фундаментальный принцип помогает понять, почему свет огибает препятствия. Хотя в его основе лежит интерференция вторичных волн, мы рассмотрим именно дифракционный аспект этого явления.
Представьте, что каждая точка волнового фронта становится мини-источником новых волн. Когда световая волна достигает препятствия (например, края щели), каждая точка этого края начинает излучать вторичные сферические волны. Это и есть основная идея Христиана Гюйгенса, сформулированная еще в XVII веке.
Огюстен Френель в XIX веке добавил к этому принципу важное уточнение: все эти вторичные волны являются когерентными и интерферируют между собой. В одних точках пространства они усиливают друг друга (максимумы интенсивности), в других — гасят (минимумы интенсивности).
Математическое выражение
Формула распределения интенсивности при дифракции на щели в зоне Фраунгофера:
где:
- I(θ) — интенсивность света под углом θ;
- I0 — интенсивность в центре картины (θ = 0);
- a — ширина щели;
- λ — длина световой волны;
- θ — угол наблюдения.
Это уравнение показывает, что интенсивность света убывает по мере удаления от центра дифракционной картины, образуя характерные светлые и темные полосы.
Принцип Гюйгенса-Френеля лежит в основе многих современных технологий. В вашем смартфоне датчик отпечатков пальцев использует дифракцию для точного распознавания уникальных узоров на коже. В медицине на его основе создают лазерные скальпели и диагностические томографы, где важно контролировать распространение светового пучка.
На производствах дифракционные явления применяют в системах лазерной резки металлов и автоматического контроля качества. Даже привычные 3D-кинотеатры и голографические шоу работают благодаря способности света огибать препятствия и создавать сложные интерференционные картины.
Дифракционная решетка
Если взглянуть на поверхность компакт-диска под ярким светом, заметны радужные переливы. Этот красивый эффект возникает благодаря тому, что микроскопические дорожки на диске работают как дифракционная решетка — один из самых важных оптических приборов, основанный на явлении дифракции.

Дифракционная решетка представляет собой поверхность с множеством одинаковых параллельных щелей или штрихов, расположенных на строго определенном расстоянии друг от друга. Когда свет проходит через решетку или отражается от нее, происходит удивительное явление — волны, прошедшие через разные щели, усиливают или ослабляют друг друга в зависимости от направления.
Для практических расчетов обычно рассматривают только условия максимумов, так как именно они дают яркие, хорошо наблюдаемые полосы.
Порядок максимума (m) — целое число, определяющее, во сколько раз разность хода лучей от соседних штрихов решетки превышает длину волны света.
Ключевой закон, описывающий работу решетки, выражается простой формулой:
где:
- d — период решетки (расстояние между соседними штрихами);
- θ — угол наблюдения;
- m — порядок спектра (целое число);
- λ — длина световой волны.

Рассмотрим прозрачную дифракционную решетку — она содержит множество узких щелей шириной a, разделенных непрозрачными промежутками b. Период решетки d (расстояние между центрами соседних щелей) равен сумме d = a + b. На практике период часто выражают через количество штрихов N на 1 мм: d = 1/N.
При прохождении света через такую решетку наблюдается ряд характерных особенностей.
- Нулевой порядок (m = 0)
Свет проходит прямо, без отклонения (θ = 0°). Все волны складываются в фазе, давая самый яркий максимум. Если свет белый, он остается неизменным, без разложения в спектр.
- Первый порядок (m = ±1)
Свет отклоняется на угол θ, при котором разность хода между соседними штрихами равна одной длине волны (mλ = λ). Для белого света дает радужный спектр (фиолетовый ближе к центру, красный дальше). Максимумы расположены симметрично справа и слева от нулевого порядка.
- Второй порядок (m = ±2)
Угол отклонения больше, так как разность хода — две длины волны (2λ). Спектры менее яркие и более широкие. Для белого света возможны наложения цветов, например фиолетовый из m=2 может совпасть с красным m=1.
- Высшие порядки (m = ±3, ±4 и так далее)
Еще больше отклонение, но интенсивность падает. Максимальный порядок ограничен условием ∣m∣ ≤ d/λ, иначе sinθ стал бы больше 1, что невозможно.
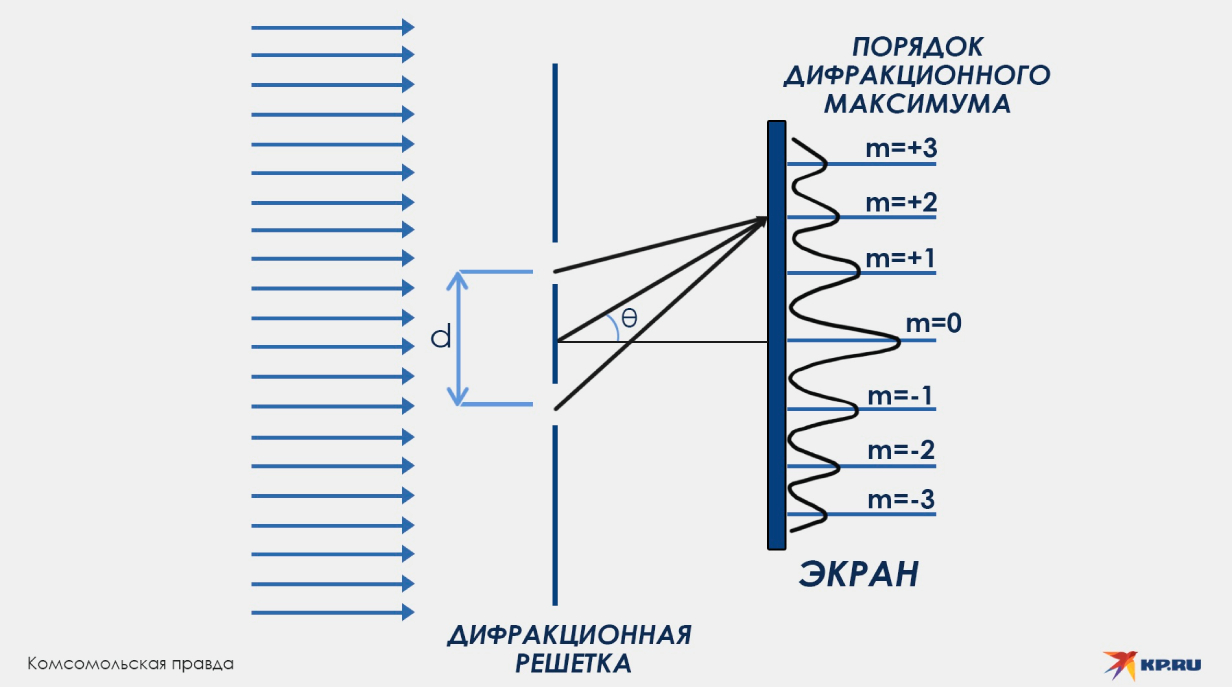
Так почему же появляются цвета? Разные цвета, а точнее длины волн, отклоняются по-разному. Например, фиолетовый свет — коротковолновый, отклоняется меньше, красный свет отклоняется больше, являясь длинноволновым. Поэтому белый свет раскладывается в радужный спектр, причем для каждого порядка m будет свой набор цветных полос. Именно это мы и видим на CD-диске — каждая радужная полоска соответствует определенному порядку дифракции.
Примеры дифракции света в повседневной жизни
Дифракция света — это не просто абстрактное физическое понятие. Мы сталкиваемся с ее проявлениями ежедневно, часто не осознавая этого. Давайте рассмотрим самые наглядные примеры.
- Ореолы вокруг уличных фонарей в тумане
В сырую погоду вокруг источников света часто видно цветное гало. Мелкие капли воды, взвешенные в воздухе, создают условия для огибания световых волн. Особенно красиво это выглядит ночью, когда вокруг уличных фонарей образуется мягкое свечение с радужными оттенками по краям.
- Размытие теней
Если внимательно посмотреть на тень от острого предмета, можно заметить, что ее края никогда не бывают абсолютно четкими. Это особенно хорошо видно на примере теней от тонких объектов вроде волоса или лезвия бритвы.
- Эффект «звездочек» на фотографиях
У ярких точечных источников света образуются «звездочки» при попытке сфотографировать их. Это результат дифракции на лепестках диафрагмы фотоаппарата. Чем сильнее закрыта диафрагма, тем более выраженными становятся эти лучи. Количество лучей в звездочке соответствует количеству лепестков диафрагмы в объективе.
- Голографические изображения на защитных элементах
Особый интерес представляют голографические изображения на банкнотах и документах для защиты. В их основе лежат сложные дифракционные структуры, которые создают объемные картинки, меняющиеся при повороте. Это одно из самых технологичных применений дифракционных явлений в повседневной жизни.
Задачи по теме «Дифракция света»
Закрепим изученный материал на практике. Перед вами несколько задач по дифракции света, которые помогут лучше понять это явление.
Задача 1
Можно ли наблюдать дифракцию солнечного света на карандаше толщиной 7 мм? Ответ поясните.
Задача 2
На дифракционную решетку с периодом 2 мкм падает красный свет (λ = 650 нм). Под каким углом будет наблюдаться максимум первого порядка (m = 1)?
Задача 3
На дифракционную решетку, имеющую 100 штрихов на 1 мм, падает нормально параллельный пучок монохроматического света с длиной волны 500 нм. Каков период этой решетки и под каким углом наблюдается максимум второго порядка? Период укажите в микрометрах, значение угла округлите до целого.
Ответы к задачам
Проверьте свои решения с помощью ответов, представленных ниже.
Задача 1
Нет, нельзя. Дифракция четко наблюдается, когда размер препятствия сравним с длиной волны света (400-700 нм). Толщина карандаша 7 мм, что равно 7 000 000 нм. Это на несколько порядков больше, поэтому дифракция не будет заметна.
Ответ: нет, нельзя
Задача 2
Используем формулу для дифракционной решетки:
dsinθ = mλ
Ответ: 19°
Задача 3
Находим период решетки: d = 1мм : 100 = 0,01 мм = 10-5 м = 10 мкм
Применяем формулу максимумов дифракционной решетки:
dsinθ = mλ
Ответ: 10 мкм; 6°
Популярные вопросы и ответы
Отвечает Анастасия Заслонова, учитель физики первой квалификационной категории:









