Касательная к окружности
Разберемся, что такое касательная к окружности, какими свойствами она обладает и как они помогают решать задачи
Касательная — это не просто прямая, которая касается окружности. Это мост между миром прямых линий и миром кривых, обладающий уникальными свойствами, которые делают вычисления неожиданно простыми.
В этой статье мы разберем, что такое касательная, изучим ее ключевые свойства и научимся применять их для решения широкого круга геометрических задач.
Что такое касательная к окружности в геометрии
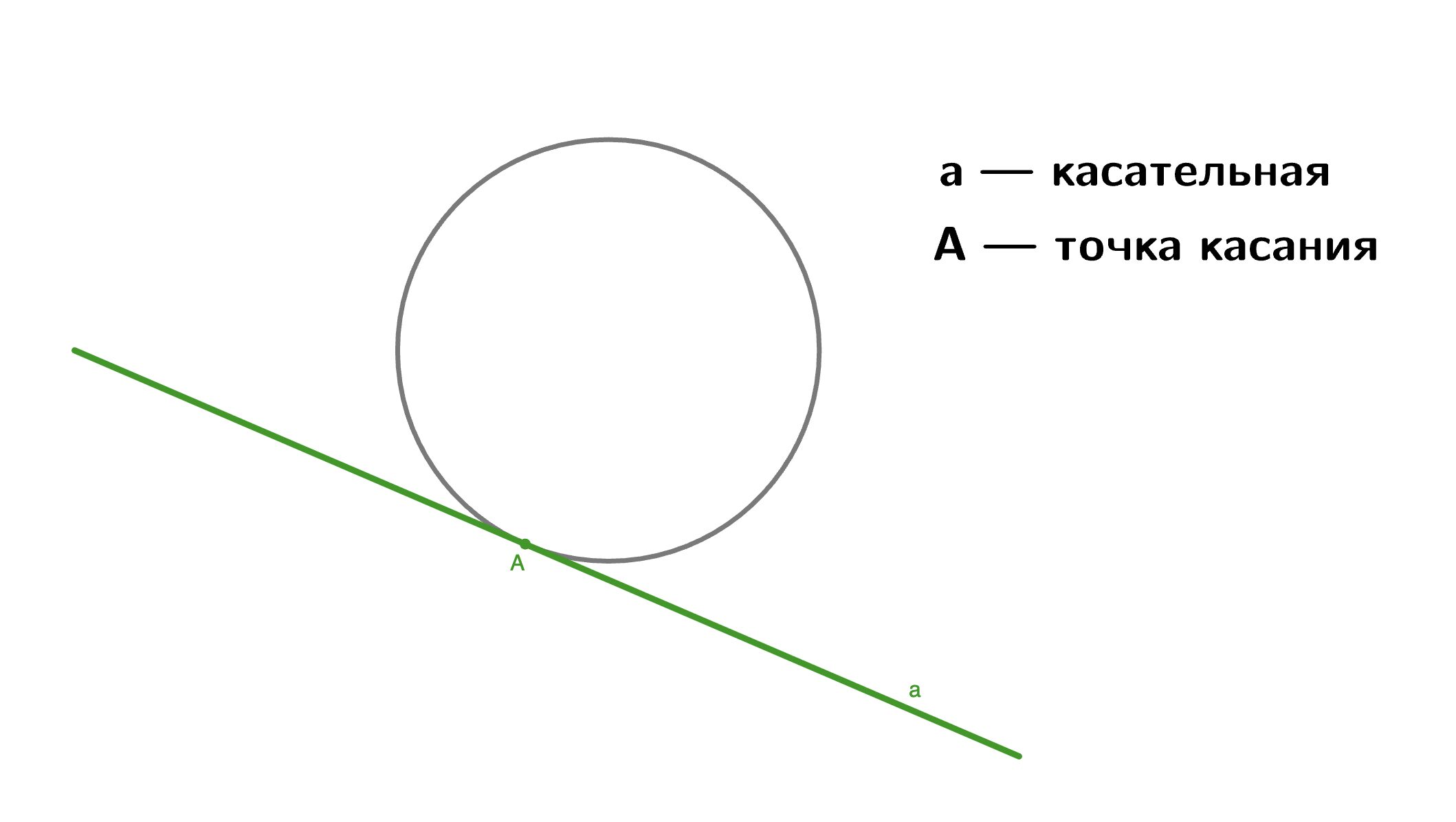
Касательная к окружности — это прямая, которая имеет с окружностью ровно одну общую точку — точку касания. Все остальные прямые либо не имеют общих точек с окружностью, либо являются секущими и пересекают ее в двух точках. Касательная — это предельный случай секущей, когда две точки пересечения сливаются в одну.
Полезная информация о касательной к окружности
Чтобы уверенно работать с касательными, важно не просто заучить свойства, а понимать их геометрический смысл. Следующая таблица-шпаргалка поможет быстро восстановить в памяти ключевые особенности этого понятия и увидеть логику их взаимосвязи.
| Касательная к окружности | Геометрическая интерпретация |
| Определение | Прямая, имеющая с окружностью только одну общую точку |
| Точка касания | Единственная общая точка касательной и окружности |
| Связь с секущей | Касательная — это предельный случай секущей, когда две точки пересечения сливаются в одну |
Свойства касательной к окружности
Касательная обладает набором свойств, которые устанавливают четкие связи между отрезками, углами и дугами. Разберем каждое свойство ниже.
это интересно
Теорема Пифагора
Вспомним главную теорему геометрии, которая связывает стороны прямоугольного треугольника
подробнее
Свойство касательной и радиуса
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
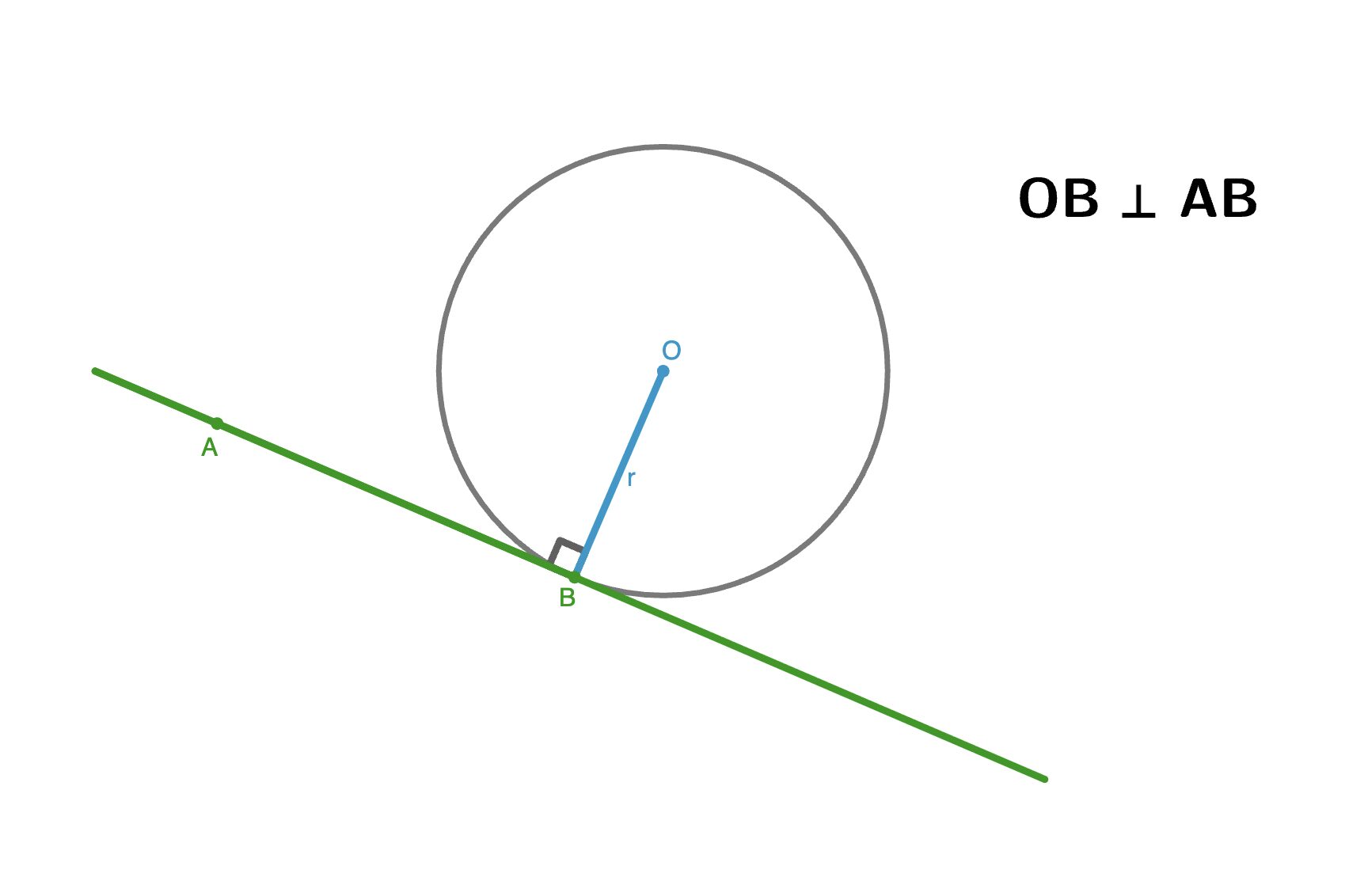
Это основное свойство, которое часто используется для доказательства перпендикулярности прямых в конструкциях с окружностями.
Свойство двух касательных, проведенных из одной точки
Если из одной точки, лежащей вне окружности, проведены две касательные, то их отрезки от этой точки до точек касания равны.
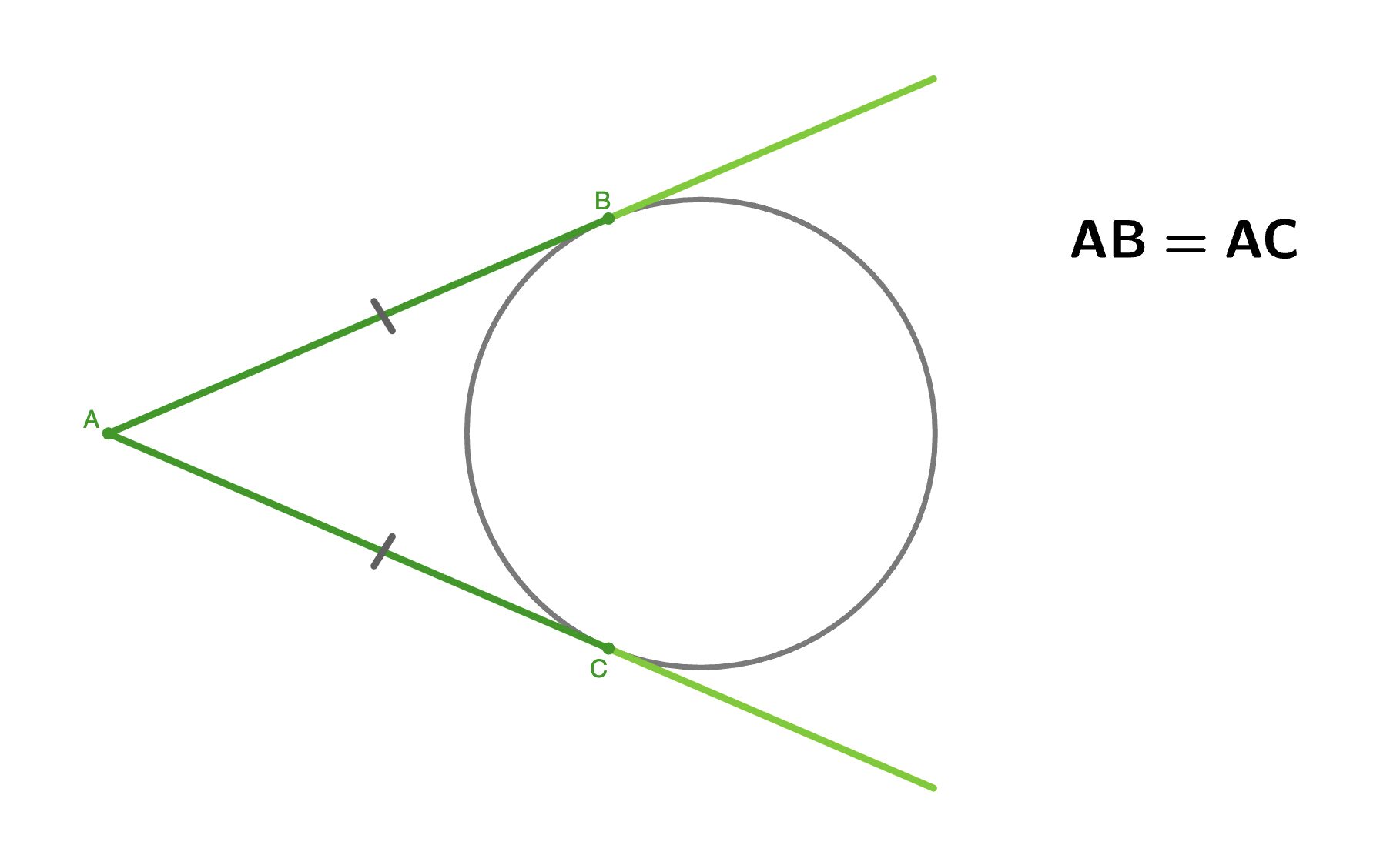
Кроме того, луч, проведенный из этой внешней точки через центр окружности, является биссектрисой угла между касательными.
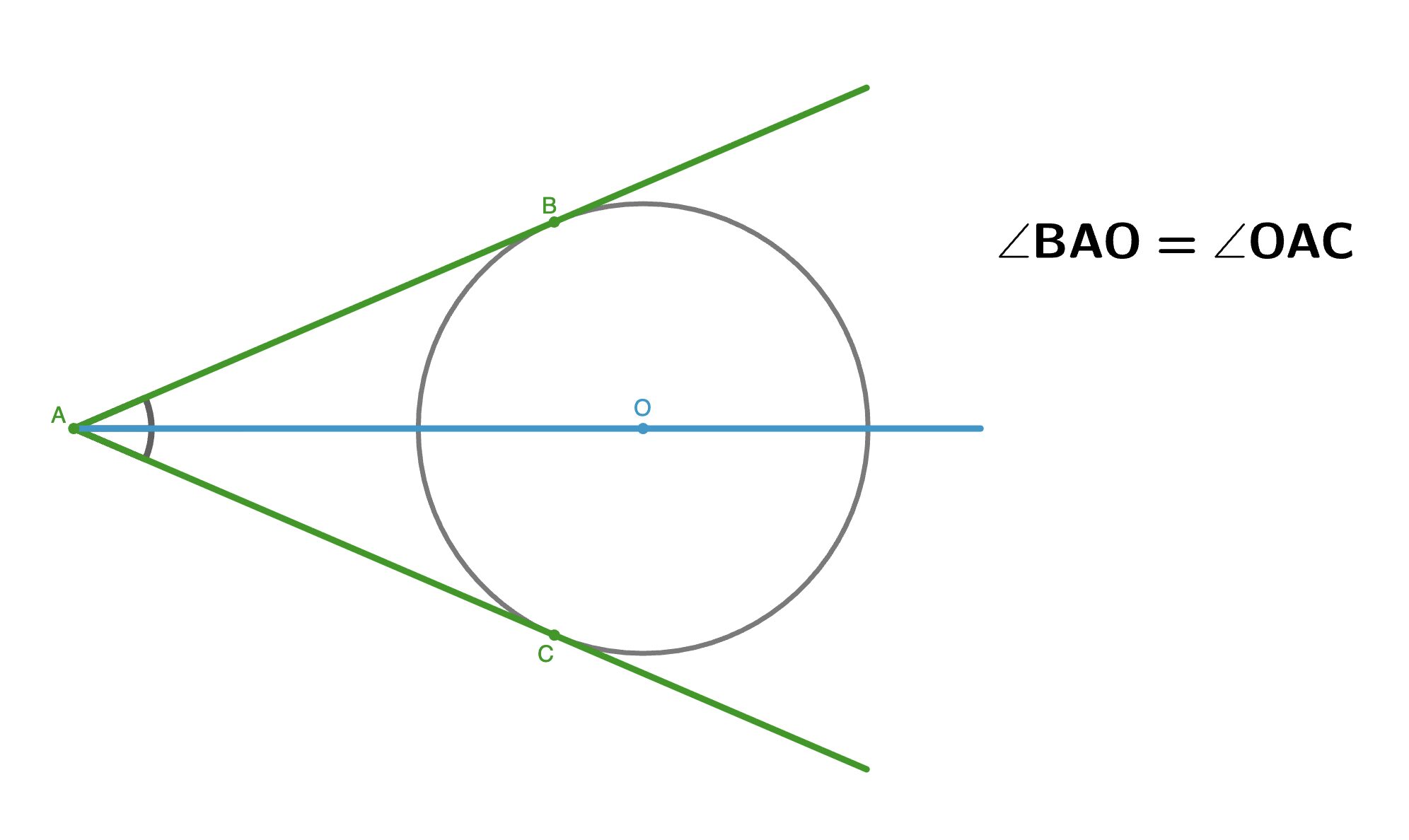
Свойство касательной и секущей
Если из одной точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины отрезка касательной равен произведению длины всей секущей на длину ее внешней части.
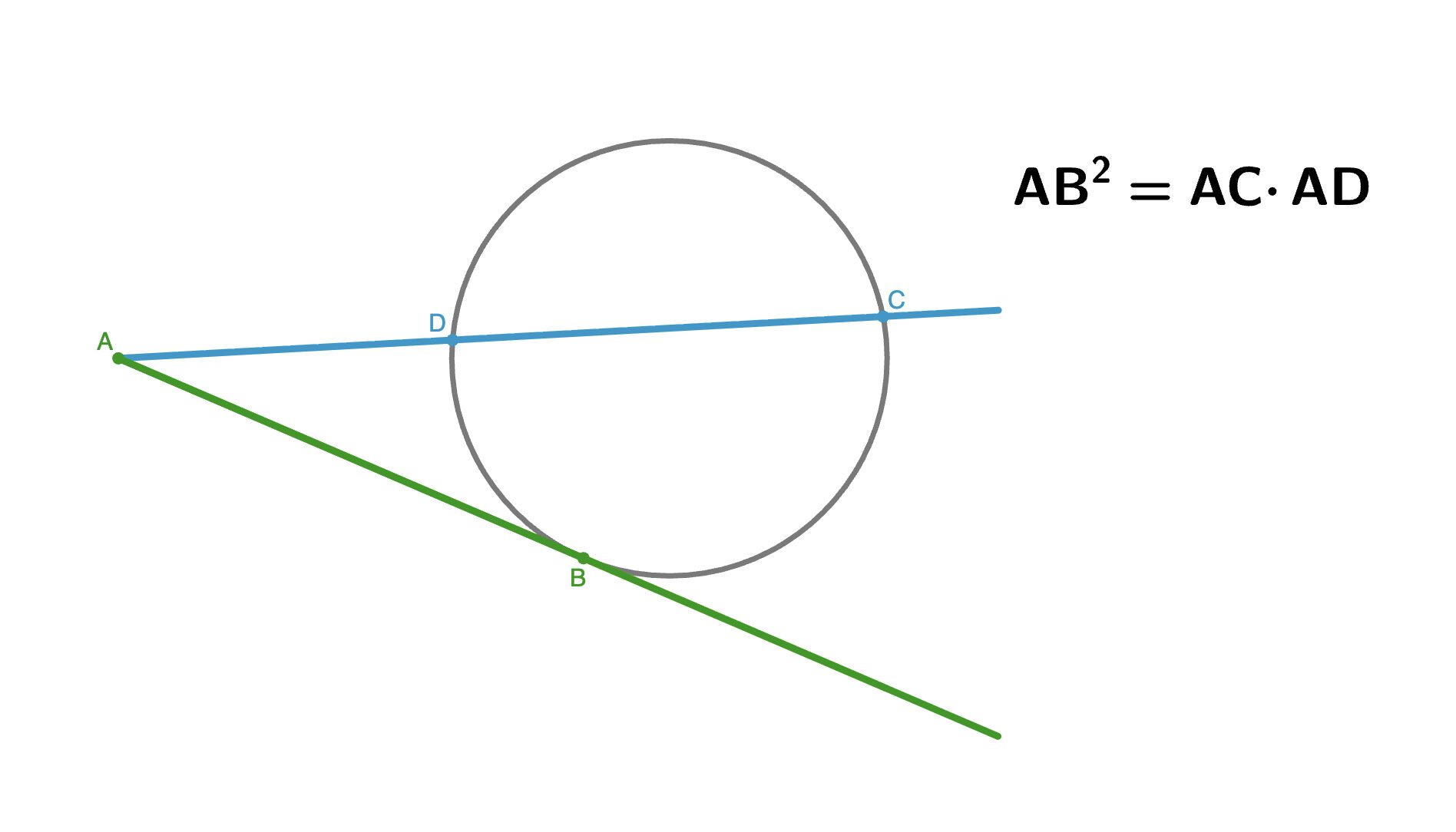
Это свойство позволяет находить длины отрезков, не прибегая к сложным вычислениям.
Свойство касательной и хорды
Угол между касательной и хордой, проведенной через точку касания, равен половине дуги, которую стягивает хорда.
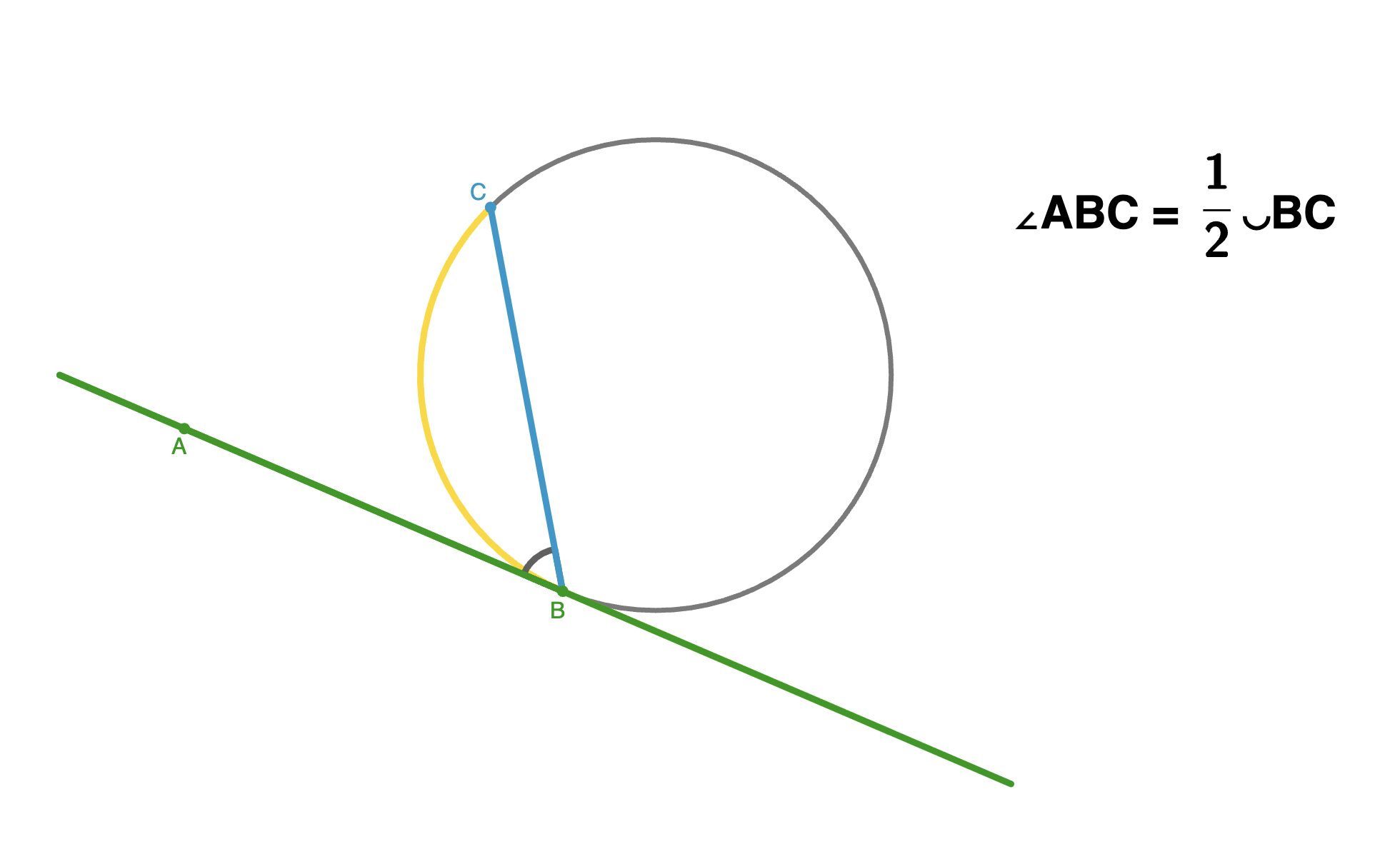
Этот угол также равен любому вписанному углу, опирающемуся на ту же хорду с противоположной стороны или половине центрального угла, опирающегося на эту хорду.
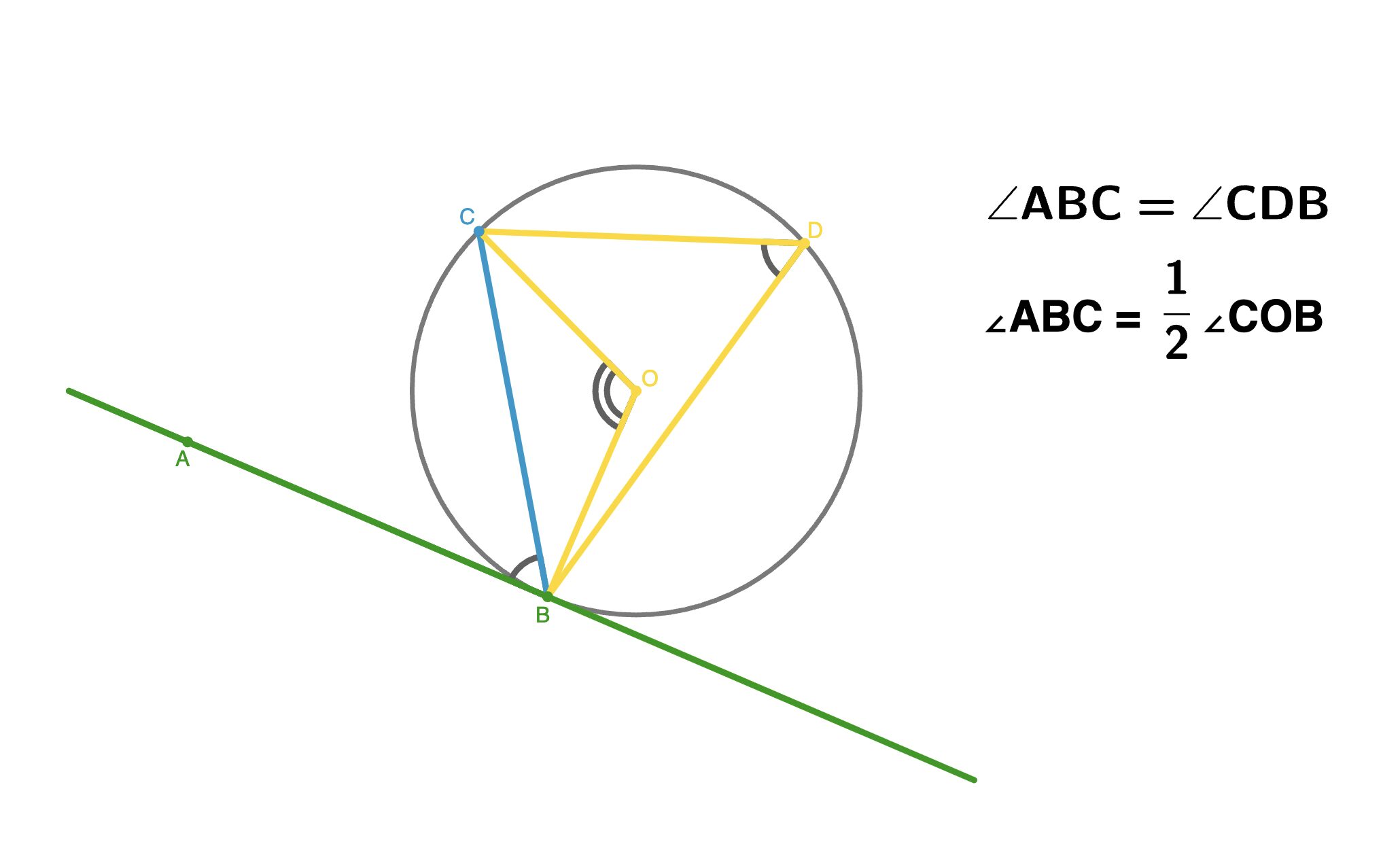
Это свойство связывает теорию касательных с теорией центральных и вписанных углов, открывая новые возможности для решения задач.
Задачи и ответы по теме «Касательная к окружности»
Теория оживает, когда применяется к реальным задачам. Решите эти упражнения, чтобы научиться видеть изученные свойства в разных геометрических конфигурациях и уверенно их применять. А также проверьте себя — после каждой задачи представлены решение и ответ.
Задача 1
К окружности с центром O проведена касательная MA, A — точка касания. Найдите угол OMA, если известно, что ∠AOM = 60°.
Решение и ответ к задаче 1
По свойству касательной и радиуса: OA ⟂ AM, значит, ∠OAM = 90°.
В треугольнике AOM: ∠AOM = 60°, ∠OAM = 90°, следовательно, ∠OMA = 180° — (60° + 90°) = 30°.
Ответ: 30°
Задача 2
Из точки C к окружности проведены две касательные CA и CB. Найдите длину отрезка CB, если CA = 15 см.
Решение и ответ к задаче 2
По свойству двух касательных, проведенных из одной точки: CB = CA = 15 см.
Ответ: 15 см
Задача 3
Из точки к окружности проведены касательная и секущая. Длина секущей равна 16 см, а длина касательной — 8 см. Найдите длину отрезка секущей, заключенного внутри окружности.
Решение и ответ к задаче 3
Обозначим точку, из которой проведены секущая и касательная, буквой K. Точку касания обозначим N, а точки пересечения секущей с окружностью — L и M, причем L находится между K и M.
По свойству касательной и секущей: KN² = KL × KM, 82 = KL × 16, KL = 4 см.
Отрезок секущей внутри окружности: LM = KM — KL = 16 — 4 = 12 см.
Ответ: 12 см
Задача 4
К окружности проведены касательная AB и хорда BC. Найдите величину острого угла между касательной и хордой, если меньшая из дуг BC равна 80°.
Решение и ответ к задаче 4
По свойству угла между касательной и хордой:
∠ABC = ½ ◡BC
∠ABC = ½ × 80° = 40°
Ответ: 40°
Задача 5
Из точки P к окружности с центром O проведены две касательные PA и PB. Найдите угол между касательными, если угол между прямой PO и касательной PA равен 40°.
Решение и ответ к задаче 5
По свойству угла между касательной и хордой:
∠ABC = ½ ◡BC
∠ABC = ½ × 80° = 40°
Ответ: 40°
Популярные вопросы и ответы
Отвечает Анна Жадан, старший преподаватель математики, методист Домашней школы «ИнтернетУрок»:
Сколько общих точек может быть у прямой и окружности?
Три случая расположения прямой и окружности:
• прямая и окружность не пересекаются — нет общих точек;
• прямая касается окружности — общая точка только одна;
• прямая и окружность пересекаются — они имеют две общие точки.
• прямая и окружность не пересекаются — нет общих точек;
• прямая касается окружности — общая точка только одна;
• прямая и окружность пересекаются — они имеют две общие точки.
Почему тему по геометрии «Касательная к окружности» изучают в 8 классе?
В 8 классе ученики уже знакомы с такими понятиями и их свойствами, как прямая, окружность, угол, дуга, радиус, треугольник и прочее. Поэтому логичным является переход к изучению свойств касательной к окружности, где появляется умение анализировать взаимное расположение геометрических объектов, определять, как связаны касательная и радиус, какой угол образуется между радиусом и касательной в точке касания. В 8 классе учащиеся обычно осваивают геометрические построения и доказательства на более абстрактном уровне по сравнению с 7 классом.
В каких заданиях ОГЭ и ЕГЭ по математике понадобятся знания свойств касательной к окружности?
Знания о свойствах касательной к окружности необходимы для решения заданий государственных экзаменов, связанных с окружностями и кругами.
В ОГЭ знание свойств касательной к окружности пригодится для решения следующих заданий: 16, 23, 24, 25.
В ЕГЭ базового уровня по математике знания свойств касательной к окружности может понадобиться для решения следующих заданий: 8, 10, 12.
В ЕГЭ профильного уровня по математике знания свойств касательной к окружности может пригодиться для решения следующих заданий: 1, 14, 17.
В ОГЭ знание свойств касательной к окружности пригодится для решения следующих заданий: 16, 23, 24, 25.
В ЕГЭ базового уровня по математике знания свойств касательной к окружности может понадобиться для решения следующих заданий: 8, 10, 12.
В ЕГЭ профильного уровня по математике знания свойств касательной к окружности может пригодиться для решения следующих заданий: 1, 14, 17.
