Хорда окружности: что такое, формула длины хорды, свойства, задачи с ответами по геометрии для 8 класса и подготовки к ОГЭ и ЕГЭ

Хорда окружности — это отрезок, соединяющий две точки на кривой. Несмотря на простоту определения, она является важным инструментом для вычислений и доказательств в геометрии. Ее свойства позволяют находить расстояния, углы и устанавливать связи между элементами окружности, что регулярно проверяется в заданиях ОГЭ и ЕГЭ. В этой статье мы разберем, какими свойствами обладает хорда и как они помогают решать множество задач по геометрии.

Что такое хорда окружности в геометрии

Хорда окружности — это отрезок, соединяющий две точки окружности.

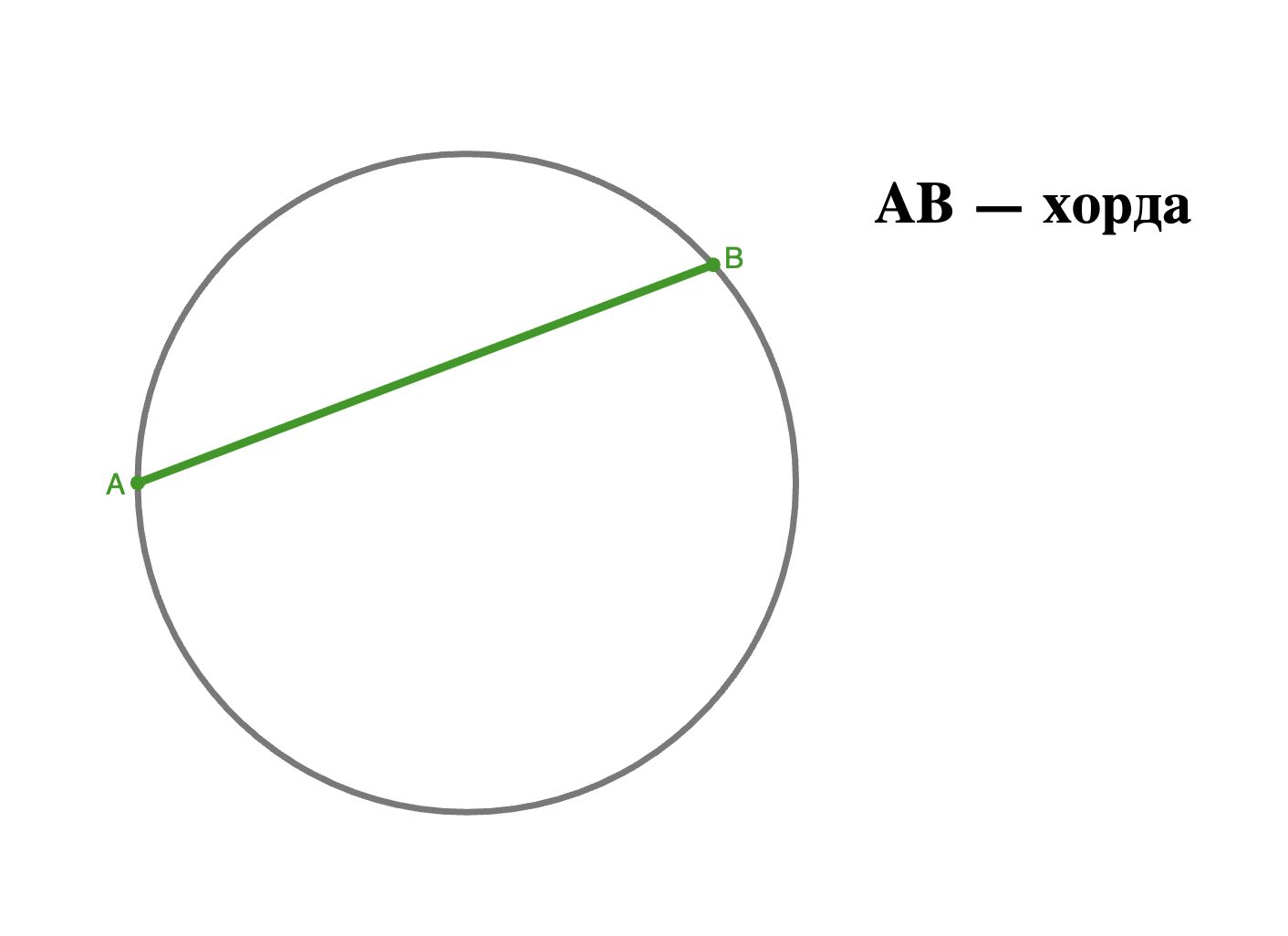
Хорда окружности. Изображение: Ирина Соколова

Если хорда проходит через центр окружности, она называется диаметром и является самой длинной хордой в окружности.

Полезная информация о хорде окружности

Чтобы уверенно работать с хордами, важно не просто заучить свойства, а понимать их геометрический смысл. Следующая таблица-шпаргалка поможет быстро восстановить в памяти ключевые особенности этого понятия и увидеть логику их взаимосвязи.

Характеристика хорды окружности	Геометрическая интерпретация
Определение	Отрезок, соединяющий две точки окружности
Частный случай	Диаметр — хорда, проходящая через центр окружности
Связь с секущей	Хорда — отрезок секущей внутри окружности
Связь с дугой	Каждая хорда стягивает соответствующую дугу

Свойства хорды окружности

Хорды обладают рядом важных свойств, которые устанавливают четкие связи между длинами отрезков, углами и дугами. Такие закономерности образуют систему, где знание одного элемента позволяет определять другие. Этот системный подход особенно важен при решении задач, где требуется применить несколько свойств одновременно. Разберем каждое свойство ниже.

это интересно

Касательная к окружности

Что такое касательная к окружности и какими свойствами она обладает

подробнее

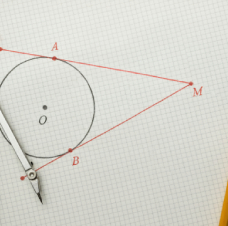
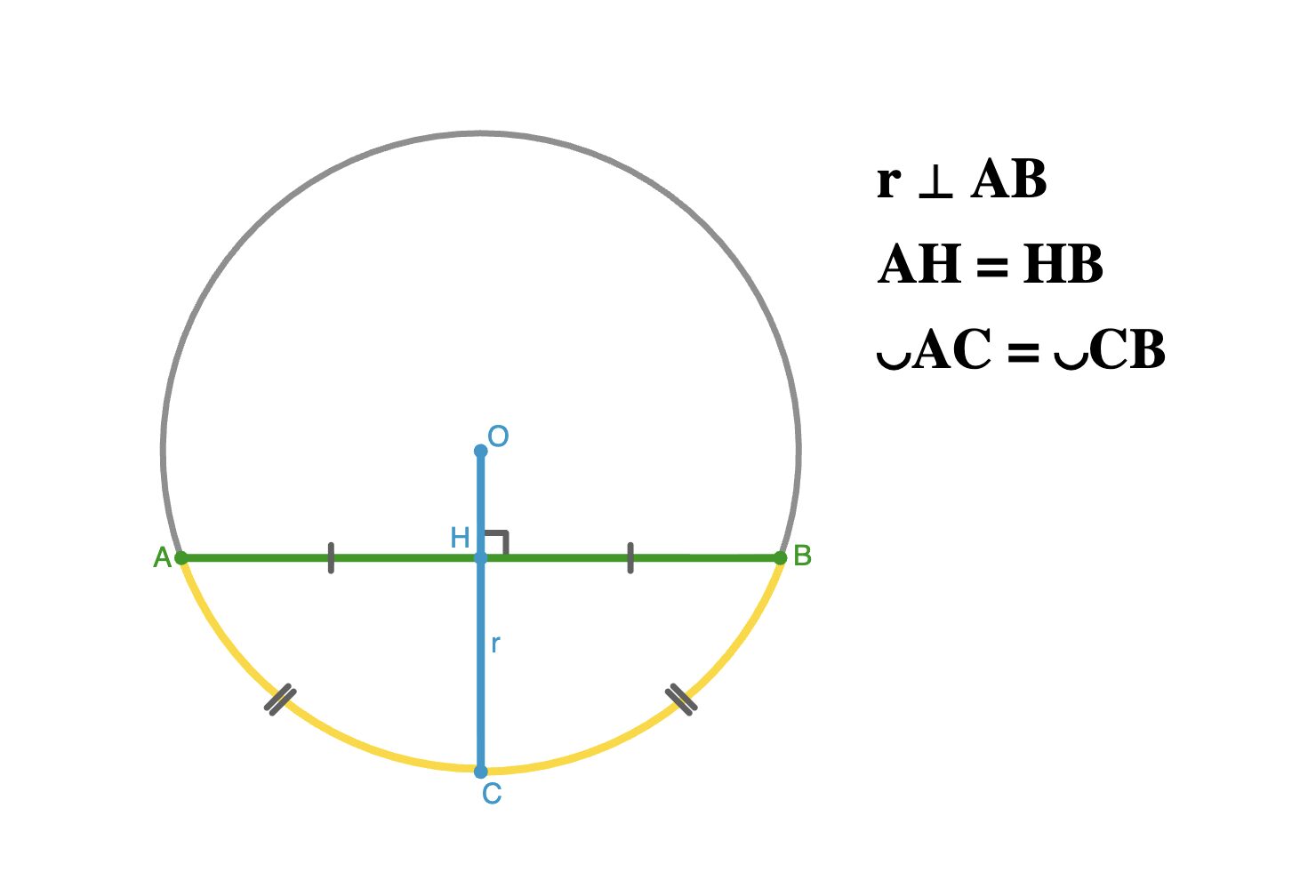
Свойство хорды и радиуса

Радиус, перпендикулярный хорде, делит ее и стягиваемые ею дуги пополам, и наоборот.

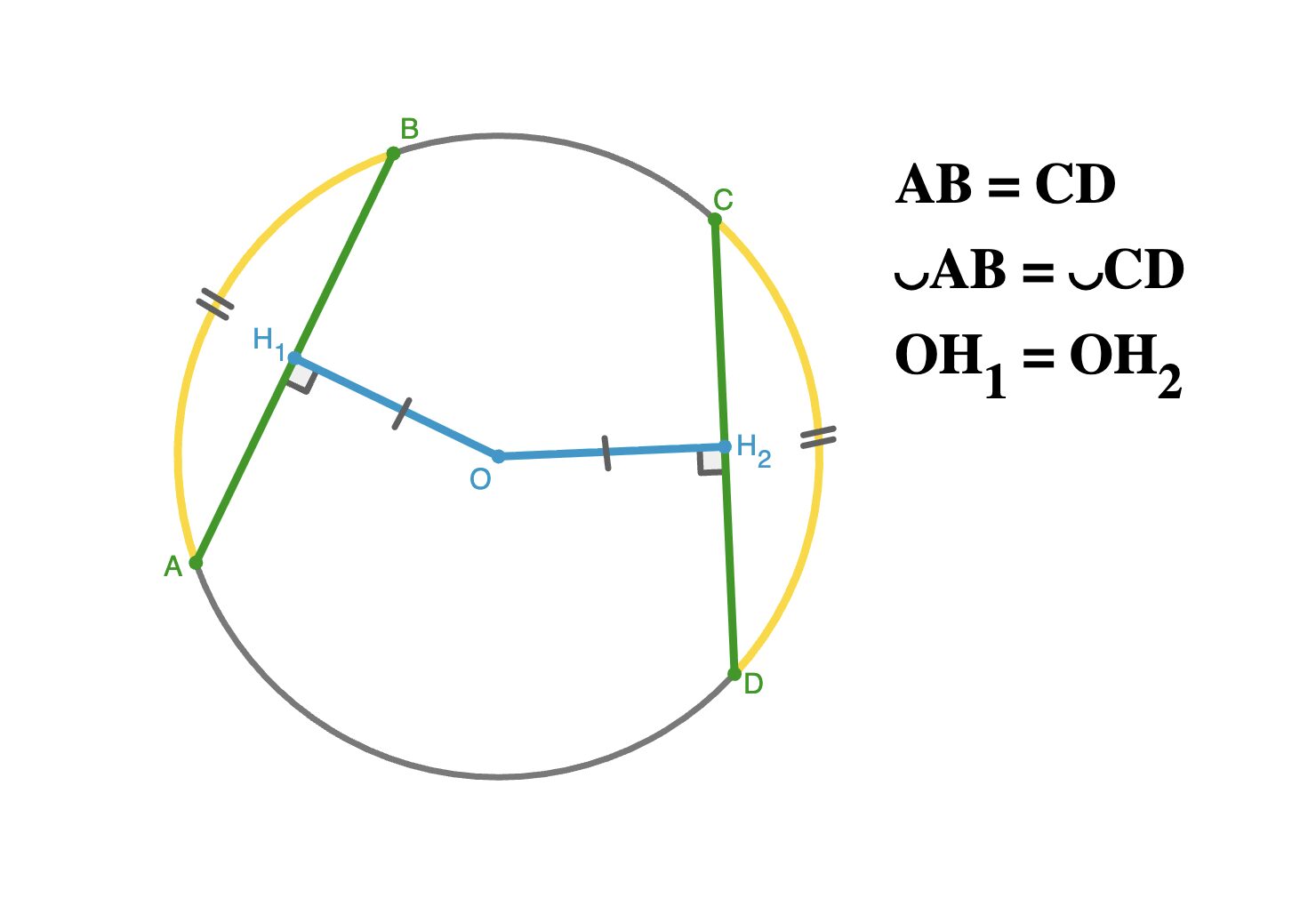
Хорда и радиус. Изображение: Ирина Соколова

Свойство равных хорд

Равные хорды стягивают равные дуги и находятся на одинаковом расстоянии от центра окружности.

Две равные хорды. Изображение: Ирина Соколова

Свойство параллельных хорд

Дуги окружности, заключенные между параллельными хордами, равны.

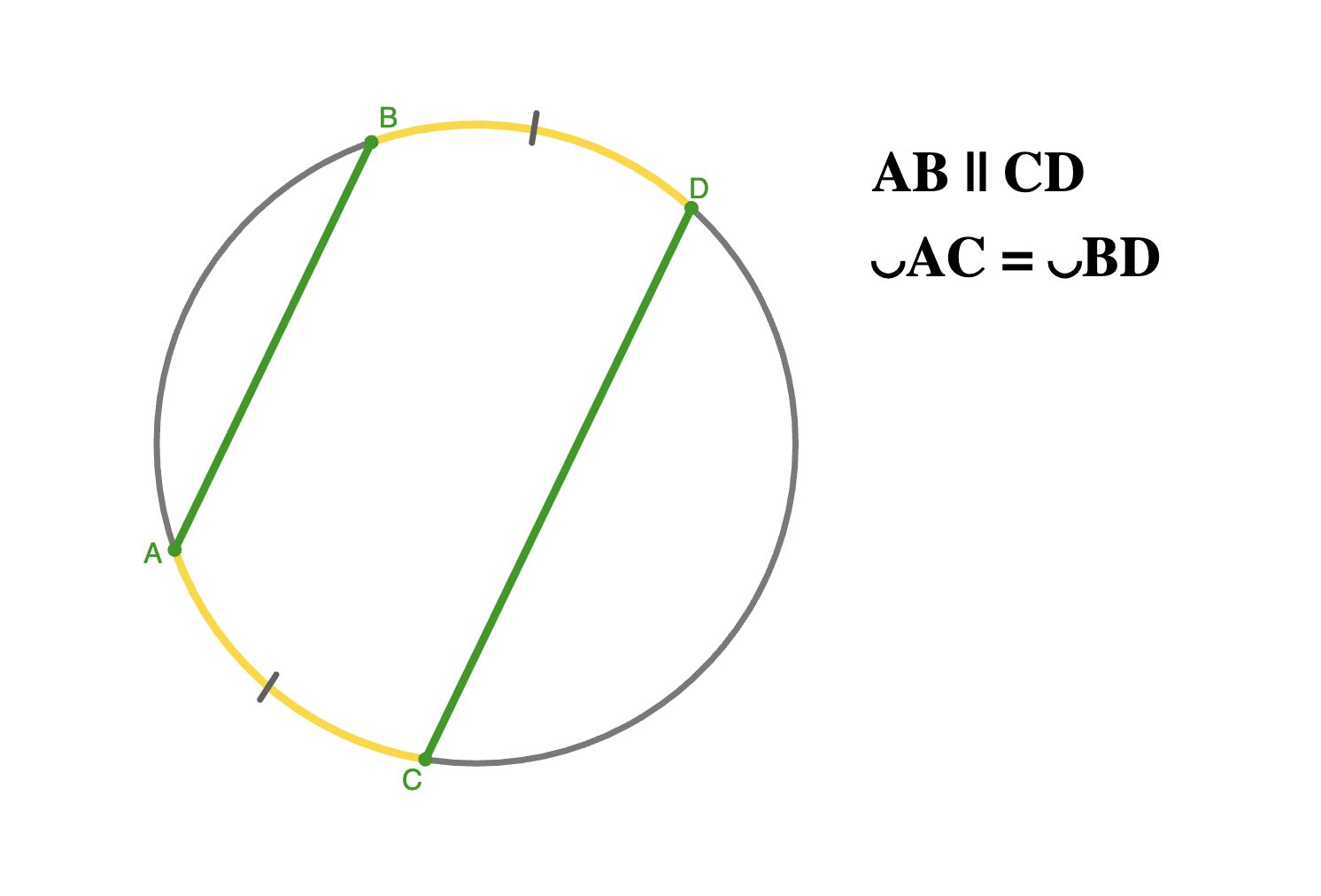
Две параллельные хорды. Изображение: Ирина Соколова

Свойство пересекающихся хорд

Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

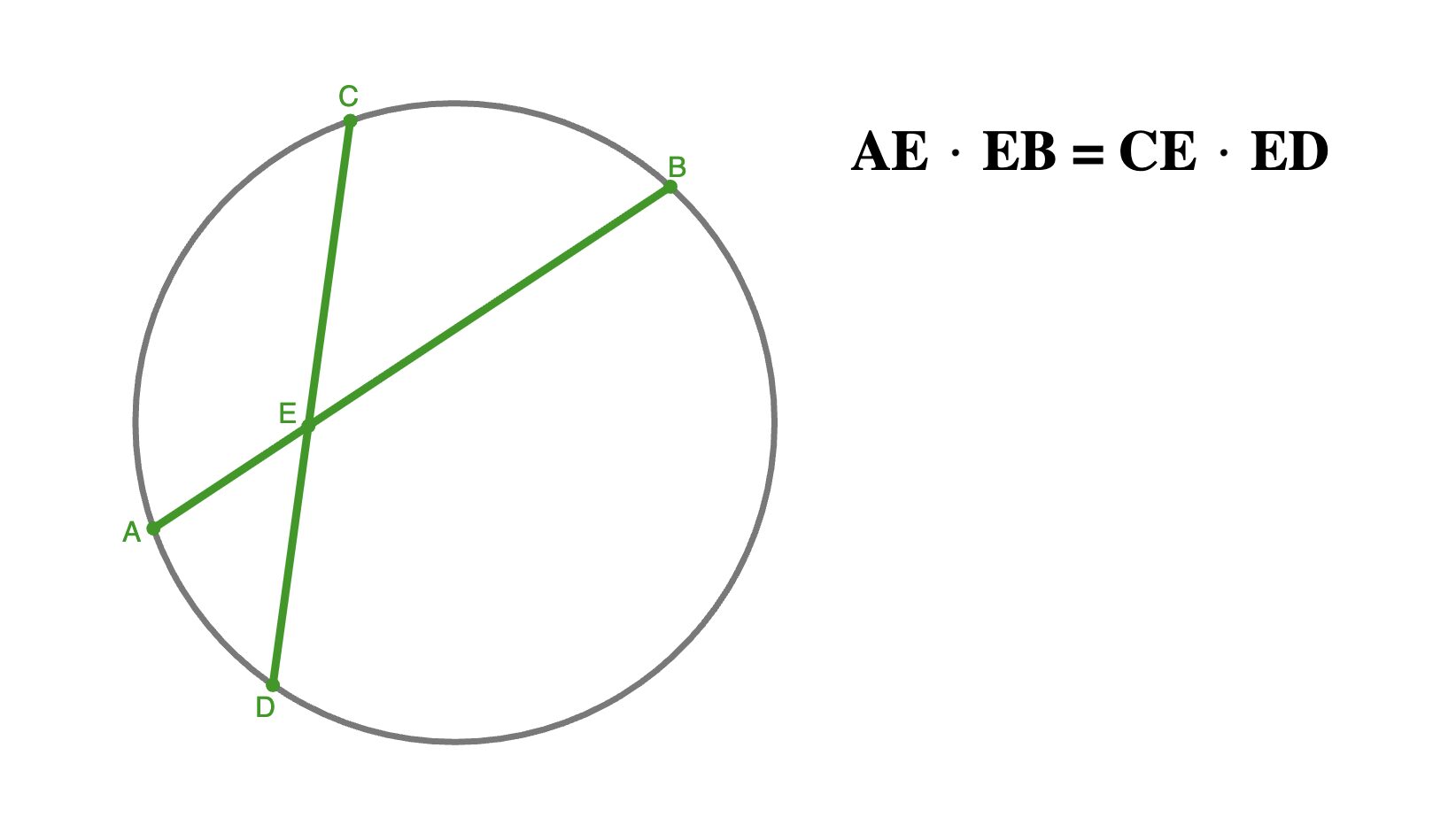
Две пересекающиеся хорды. Изображение: Ирина Соколова

Также при пересечении хорд образуются две пары подобных треугольников.

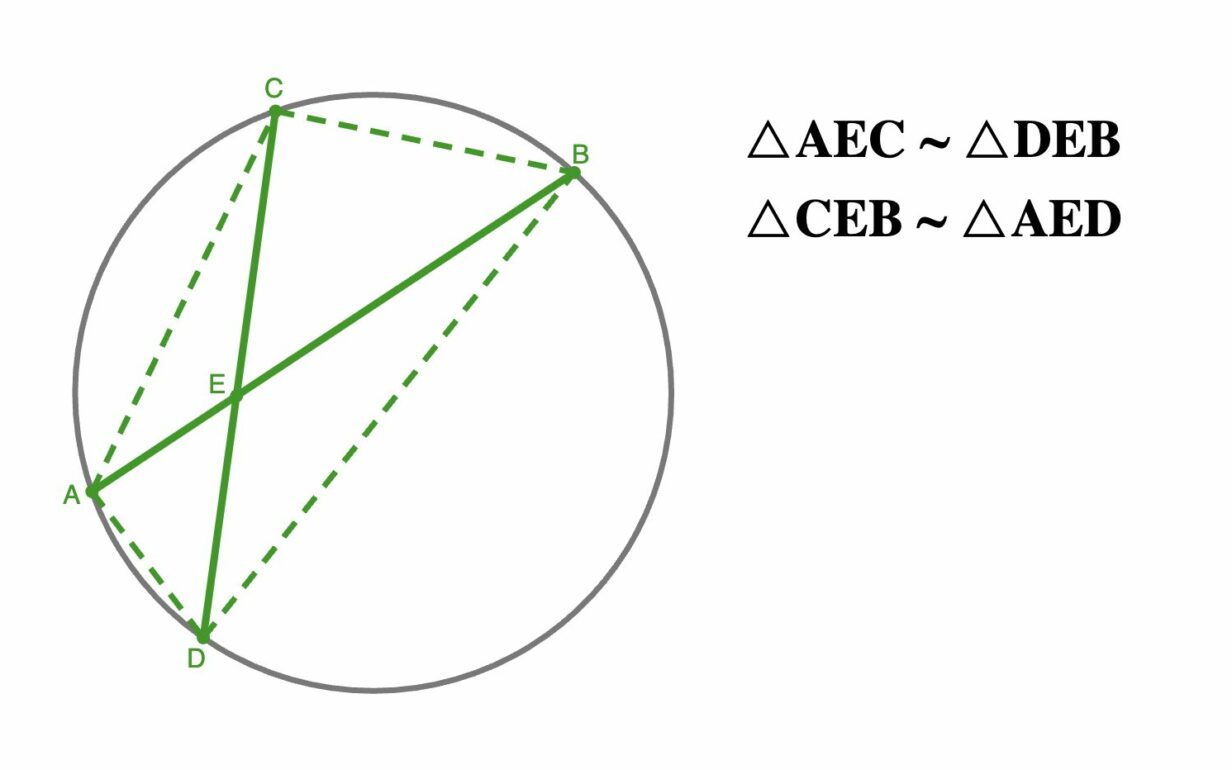
Две пересекающиеся хорды и образованные ими треугольники. Изображение: Ирина Соколова

Формулы длины хорды окружности

Для вычисления длины хорды можно использовать несколько формул в зависимости от известных параметров. Эти формулы позволяют находить решение быстрее.

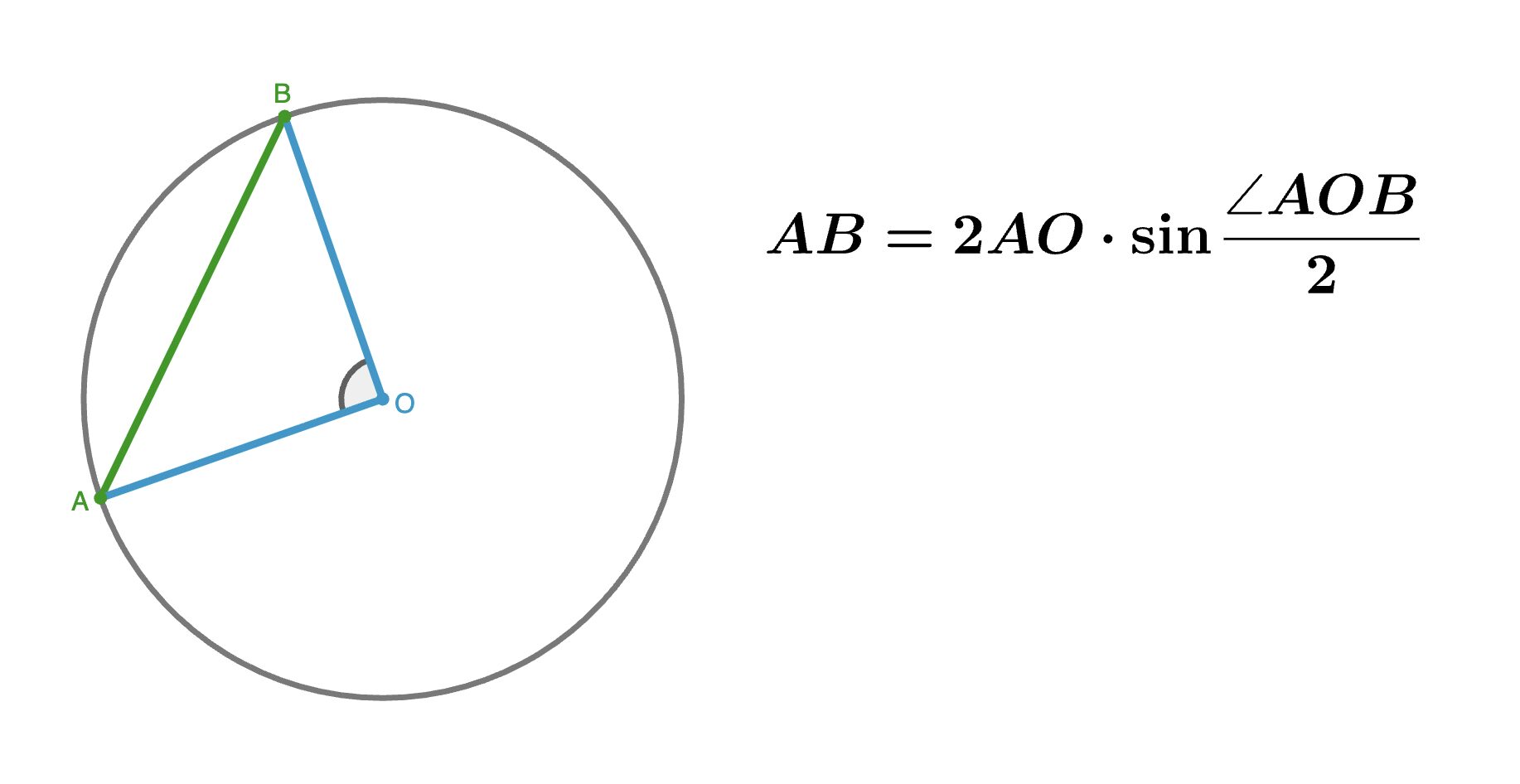
Через радиус и центральный угол, опирающийся на хорду

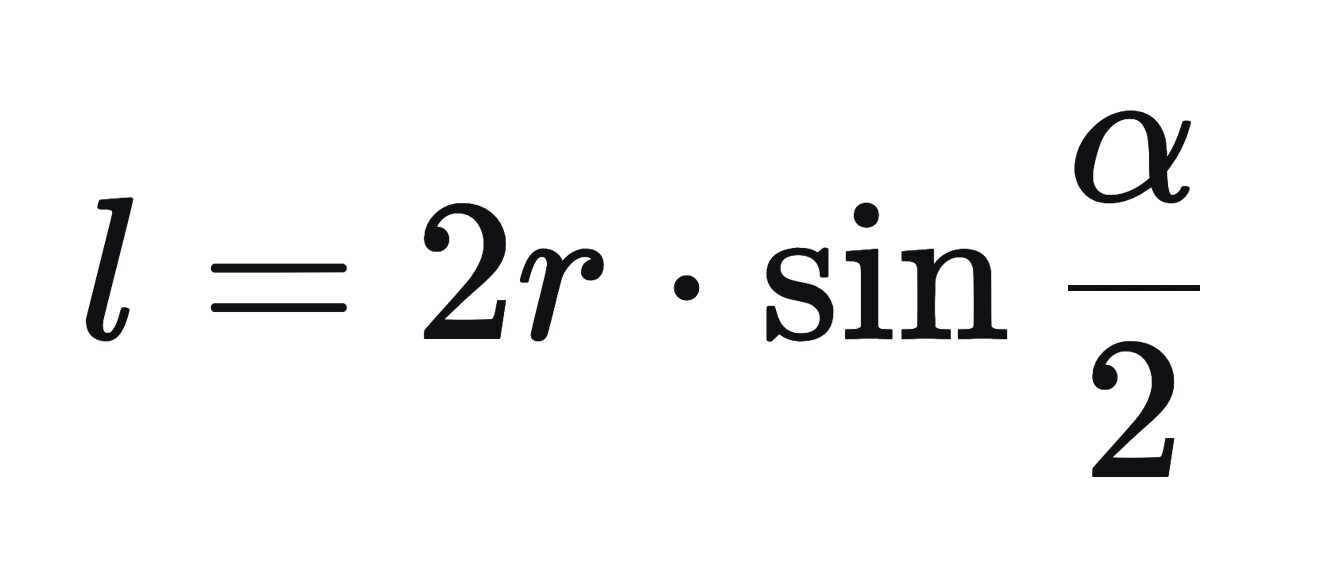
где:

l — длина хорды
r — радиус
α — центральный угол, опирающийся на хорду

Зависимость длины хорды от радиуса и центрального угла, опирающегося на хорду. Изображение: Ирина Соколова

Через радиус и расстояние от центра до хорды

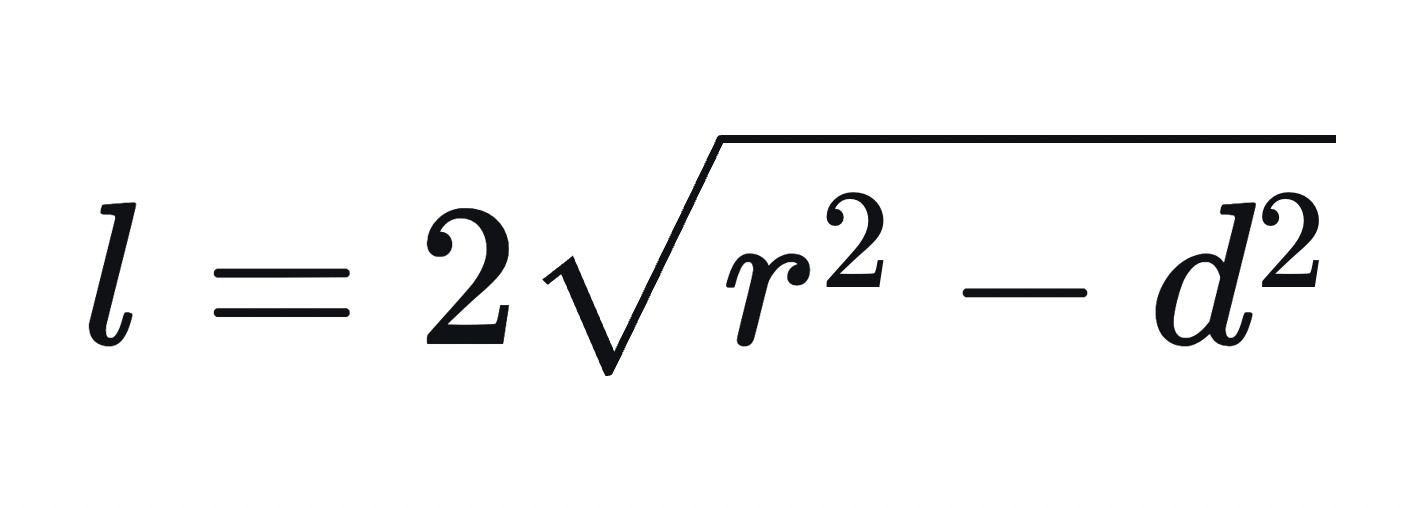
где:

l — длина хорды
r — радиус
d — расстояние от центра окружности до хорды

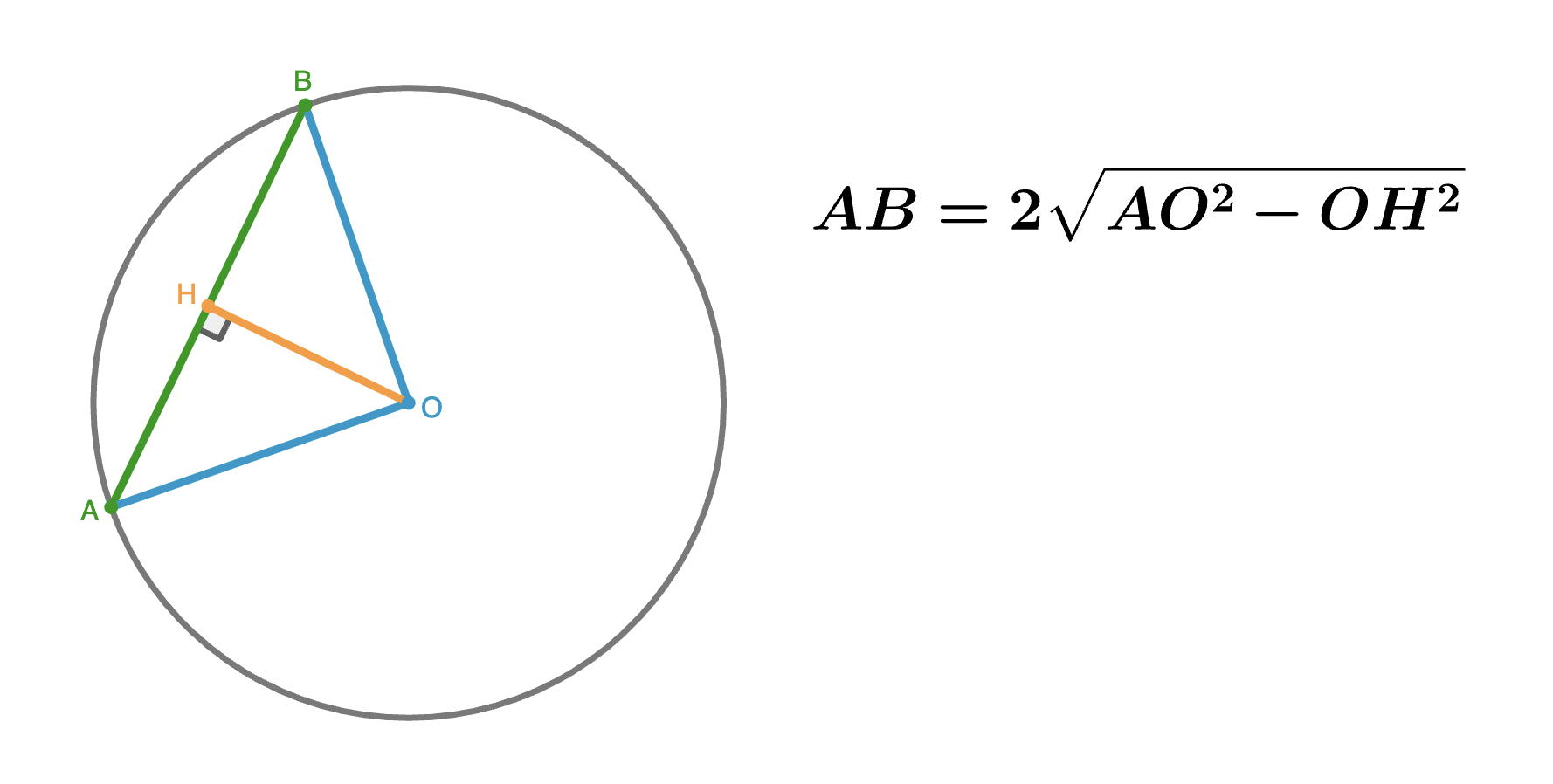
Зависимость длины хорды от радиуса и расстояния от центра окружности до хорды. Изображение: Ирина Соколова

Эти формулы легко вывести, если вы их забудете. Первая следует из теоремы синусов в равнобедренном треугольнике, образованном двумя радиусами и хордой, а вторая — прямое следствие теоремы Пифагора.

Задачи и ответы по теме «Хорда окружности»

Проверим, как работают изученные свойства хорд на практике. Решите предложенные задачи — они помогут закрепить каждый из разобранных случаев и подготовиться к экзаменам. К каждой задаче представлено подробное решение с ответом, чтобы вы могли проверить себя и разобраться в сложных моментах.

Задача 1

В окружности радиусом 13 см проведена хорда AB. Расстояние от центра окружности до хорды OH равно 5 см. Найдите длину хорды AB.

Решение и ответ к задаче 1

Расстояние OH от центра до хорды — это перпендикуляр, значит, он делит хорду AB пополам (AH = HB) и образует прямоугольный треугольник OHB.

По теореме Пифагора в треугольнике OHB:

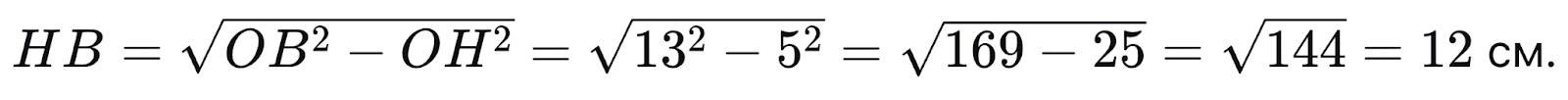
Длина всей хорды AB = 2HB = 24 см.

Ответ: 24 см

Задача 2

В окружности проведены две хорды AC и BD, которые пересекаются в точке E. Найдите длину отрезка BE, если AE = 3 см, CE = 9 см, DE = 4 см.

Решение и ответ к задаче 2

По свойству пересекающихся хорд:

AE × EC = BE × ED.

Подставляем известные значения и находим BE:

3 × 9 = BE × 4

4BE = 27

BE = 6,75 см.

Ответ: 6,75 см

Задача 3

В окружности проведены две равные хорды AB и CD. Хорда AB удалена от центра на 6 см. На каком расстоянии от центра находится хорда CD?

Решение и ответ к задаче 3

Равные хорды находятся на одинаковом расстоянии от центра окружности, значит, хорда CD удалена от центра тоже на 6 см.

Ответ: 6 см

Задача 4

В окружности проведены параллельные хорды AB и CD. Градусная мера дуги AB равна 30°, а дуги BD равна 50°. Найдите градусную меру дуги CD.

Решение и ответ к задаче 4

Дуги, заключенные между параллельными хордами, равны:

◡AC = ◡BD = 50°.

Так как полная окружность составляет 360°, то

◡CD = 360 — (◡AC + ◡AB + ◡BD) = 360° — (50° + 30° + 50°) = 230°.

Ответ: 230°

Задача 5

В окружности с радиусом 10 см проведены две параллельные хорды AB и CD по одну сторону от центра. Расстояние от центра до хорды AB равно 6 см, а до хорды CD — 8 см. Найдите расстояние между хордами.

Решение и ответ к задаче 5

Хорды расположены по одну сторону от центра, значит, расстояние между ними равно разности расстояний от центра до хорд:

8 − 6 = 2 см.

Ответ: 2 см

Задача 6

В окружности радиусом 8 см проведена хорда, стягивающая дугу в 90°. Найдите длину этой хорды.

Решение и ответ к задаче 6

Центральный угол равен градусной мере дуги, на которую он опирается. Значит, центральный угол, опирающийся на данную хорду, равен 90°.

Используем формулу длины хорды через радиус и центральный угол:

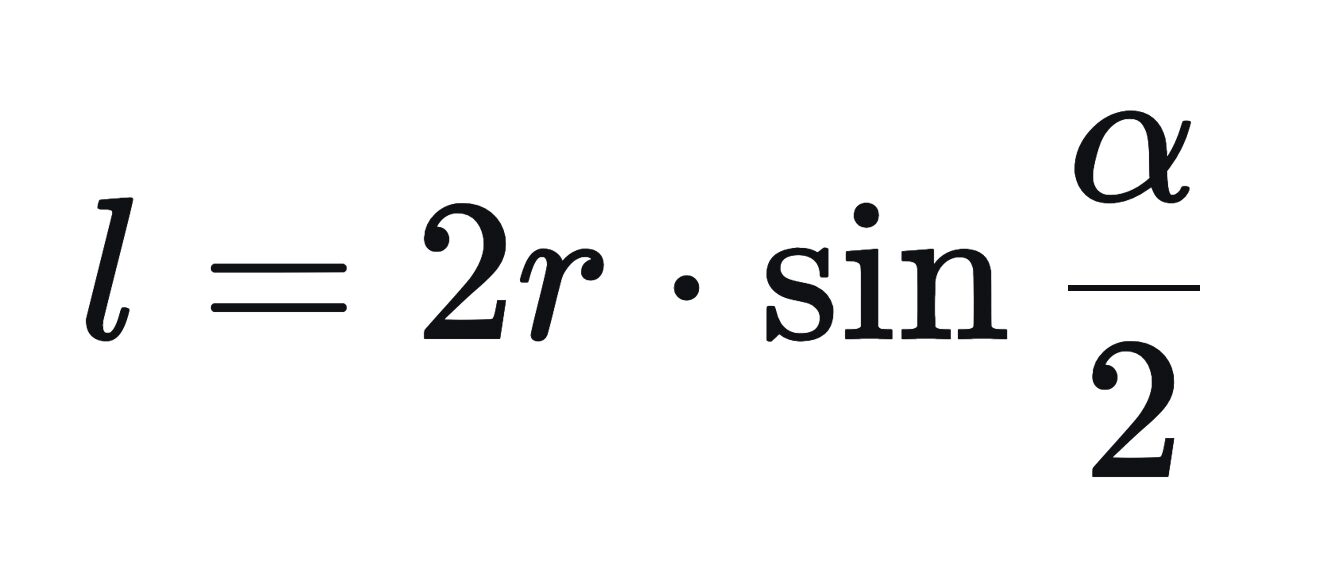
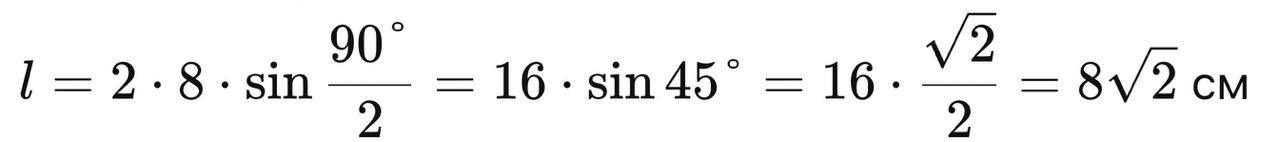
Ответ:

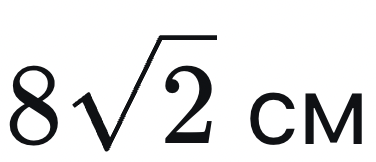
Задача 7

В окружности радиусом 10 см проведена хорда, находящаяся на расстоянии 6 см от центра. Найдите длину хорды.

Решение и ответ к задаче 7

Используем формулу длины хорды через радиус и расстояние от центра до хорды:

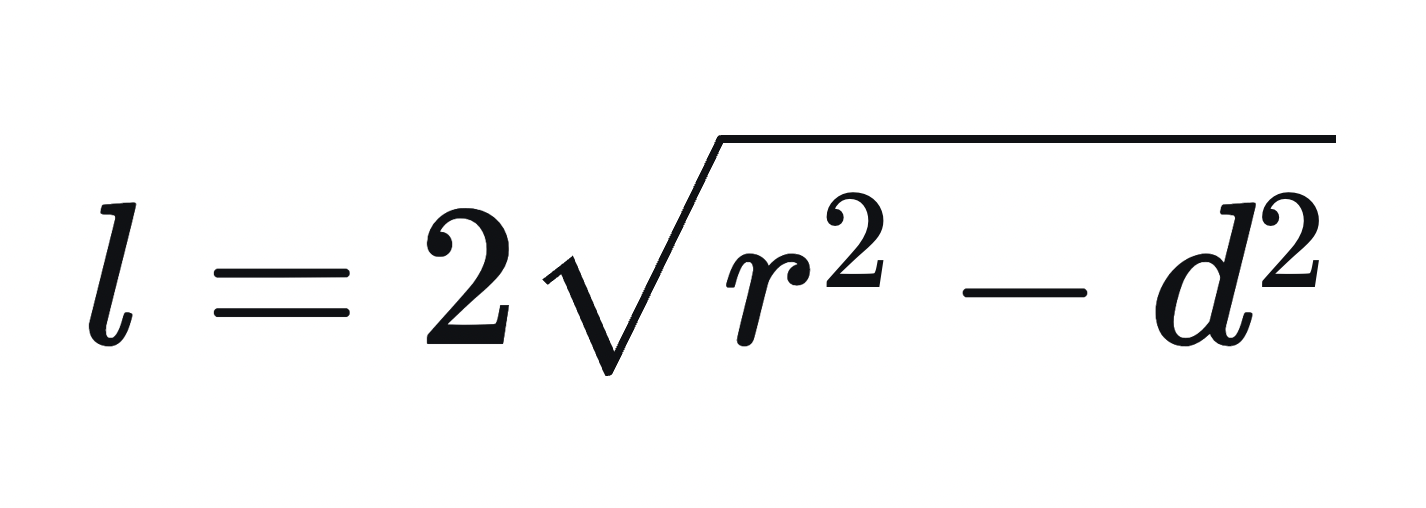
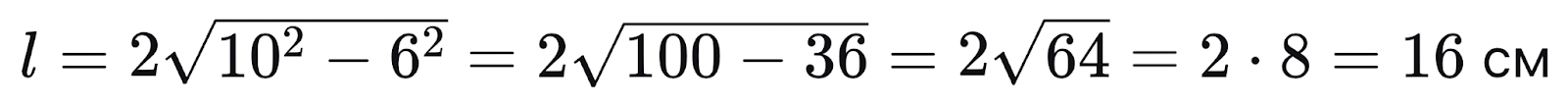
Ответ: 16 см

Популярные вопросы и ответы

Отвечает Анна Жадан, старший преподаватель математики, методист Домашней школы «ИнтернетУрок»:

Чем хорда отличается от диаметра?

Хорда — это отрезок, соединяющий любые две точки окружности. Особый случай хорды — диаметр, который всегда пересекает центр окружности. Соответственно, любая хорда, отличная от диаметра, характеризуется отсутствием обязательного прохождения через ее середину.

Почему тему по геометрии «Хорда окружности» изучают в 8 классе?

После изучения базовых геометрических понятий, углов и треугольников в седьмом классе, восьмиклассники начинают изучение окружностей. В рамках этой темы рассматриваются хорды окружности. Изучение свойств хорд помогает учащимся применять теоретические знания для решения практических задач: определения их длины, установления взаимосвязи с центральными и вписанными углами, построение геометрических конфигураций с использованием хорды и касательной.

В каких заданиях ОГЭ и ЕГЭ по математике понадобятся знания свойств хорды окружности?

Понимание свойств хорды — неотъемлемая часть успешной сдачи экзаменов по математике, так как эта тема затрагивается в заданиях всех уровней.

На ОГЭ свойства хорды применяются как в относительно простой задаче №16 первой части, так и в сложных геометрических задачах под №23, №24 и №25 из второй части.

В ЕГЭ базового уровня эти знания прежде всего необходимы для решения планиметрической задачи №12, а также могут быть полезны в задании №10 на прикладную геометрию.

Что касается ЕГЭ профильного уровня, то здесь хорда встречается на протяжении всего экзамена: от базового задания №1 в начале до сложных задач второй части — в стереометрии №14, где фигурируют круглые тела, и в одной из самых сложных задач по планиметрии №17.