Квадратные неравенства

Ранее вы уже освоили линейные неравенства, простые и понятные, где все решается за пару шагов. Теперь настало время квадратных неравенств — не менее интересных и важных.

Почему эти неравенства стоят вашего внимания? Это обязательная тема на экзаменах, без нее не обходится ни ОГЭ, ни ЕГЭ. Вы научитесь решать новые задачи, которые не поддаются линейным методам. Квадратные неравенства — это не сложно, если в них качественно разобраться.

Что такое квадратные неравенства в алгебре

Квадратное неравенство — это математическое выражение, содержащее буквенную переменную во второй степени, в котором две части связаны знаками сравнения: 

• > (больше)
• < (меньше)
• ≥ (больше или равно)
• ≤ (меньше или равно)

Общий вид квадратного неравенства с одной переменной ax² + bx + c > 0, где:

• x – переменная,
• a, b и c – действительные числа (a ≠ 0).

Полезная информация о квадратных неравенствах

В таблице ниже собраны основные типы квадратных неравенств с примерами. Обратите внимание на особенности каждого случая.

Квадратное неравенство	Пример
Строгое неравенство (> или <)	5x2 — 2x + 1 > 0
Нестрогое неравенство (≥ или ≤)	2x2 — 5x — 7 ≤ 0
Неполное неравенство (b = 0)	x2 − 9 < 0
Неполное неравенство (c = 0)	x2 − 5x ≥ 0
Неполное неравенство (b = 0, c = 0)	3x2 > 0
Двойное неравенство	1 < x2 ≤ 4

Что такое решение неравенства

Решить неравенство — значит найти все значения переменной, при которых неравенство становится верным.

Разберемся, чем отличается решение квадратных неравенств и решение квадратных уравнений. Уравнение имеет конечное число корней, а именно 0, 1 или 2. Неравенство может иметь бесконечное множество решений и целые диапазоны значений.

Рассмотрим два примера.

Уравнение: x² − 4 = 0 → x₁ = -2, x₂ = 2

Неравенство: x² − 4 > 0 → x ∈ (−∞; −2) ∪ (2; +∞)

Типы решений неравенств

Результат квадратного неравенства может быть записан различными способами. Существует три основные формы записи решений.

1. Запись в виде неравенства. Является самым простым способом представить решение. Типы записи:

• x > a, x < a — строгий ответ
• x ≥ a, x ≤ a — нестрогий ответ
• a < x < b, a ≤ x ≤ b, a < x ≤ b, a ≤ x < b — двойное неравенство

Примеры: 

x² − 9 < 0 → −3 < x < 3
x² − 5x ≥ 0 → x ≤ 0 или x ≥ 5

2. Запись в виде числового промежутка. Является более формальной математической записью.

Типы промежутков:

• (a; b) — интервал (a < x < b)
• (a; b] — полуинтервал (a < x ≤ b)
• [a; b) — полуинтервал (a ≤ x < b)
• [a; b] — отрезок (a ≤ x ≤ b)
• (-∞; a) — открытый луч (x < a)
• (a; +∞) — открытый луч (x > a)
• (-∞; a] — закрытый луч (x ≥ a)  
• [a; +∞) — закрытый луч (x ≥ a)

Примеры:

x² − 4 ≤ 0 → x ∈ [−2; 2]
x² − 3x > 0 → x ∈ (−∞; 0) ∪ (3; +∞)

3. Графическое представление. Наглядный способ изображения решения на числовой прямой.

Правила обозначений:

● — точка включается (для знаков ≥ или ≤)
○ — точка не включается (для знаков > или <)
→ или ← — направление решения

Примеры:

Для x² − 4 > 0 → x ∈ (−∞; −2) ∪ (2; +∞)

Для −x² + 9 ≥ 0 → x ∈ [−3; 3]

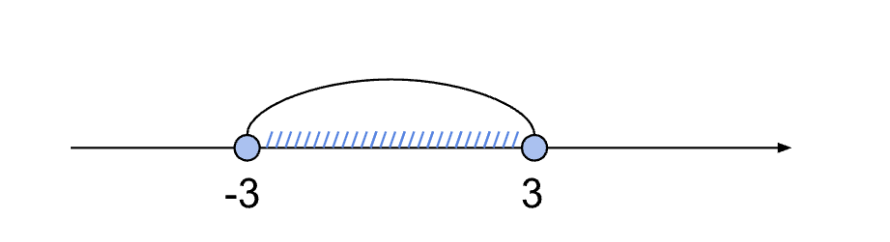
Все три формы записи равнозначны и используются в зависимости от контекста. В школьной программе часто требуется владение всеми вариантами представления решений.

Особые случаи решений

• Нет решений (x² + 1 < 0 → x ∈ ∅)
• Все действительные числа (x² ≥ 0 → x ∈ R или  x ∈ (−∞; +∞))
• Единственная точка (x² ≤ 0 → x = 0)

Методы решения квадратных неравенств

Квадратные неравенства требуют особого подхода в решении. В отличие от линейных, здесь приходится учитывать направление ветвей параболы, наличие и количество корней, а также поведение функции на разных промежутках. Рассмотрим два основных метода, каждый из которых подходит для разных типов задач и позволяет увидеть решение с разных сторон.

Метод анализа дискриминанта и направления параболы 

Универсальный метод, подходит для любых квадратных неравенств, в том числе и неполных.

Алгоритм:

1. Привести неравенство к стандартному виду: ax² + bx + c > 0.
2. Определить направление ветвей параболы с помощью значения коэффициента a:
   a > 0 — ветви вверх
   a < 0 — ветви вниз
3. Приравнять левую часть неравенства к нулю, получая уравнение: 
   ax² + bx + c = 0
4. Найти дискриминант: D = b² — 4ac.
5. Найти корни уравнения:
   D > 0: два корня x₁,x₂
   D = 0: один корень x₀
   D < 0: корней нет
6. Рассмотреть одну из возможных ситуаций и найти ответ:

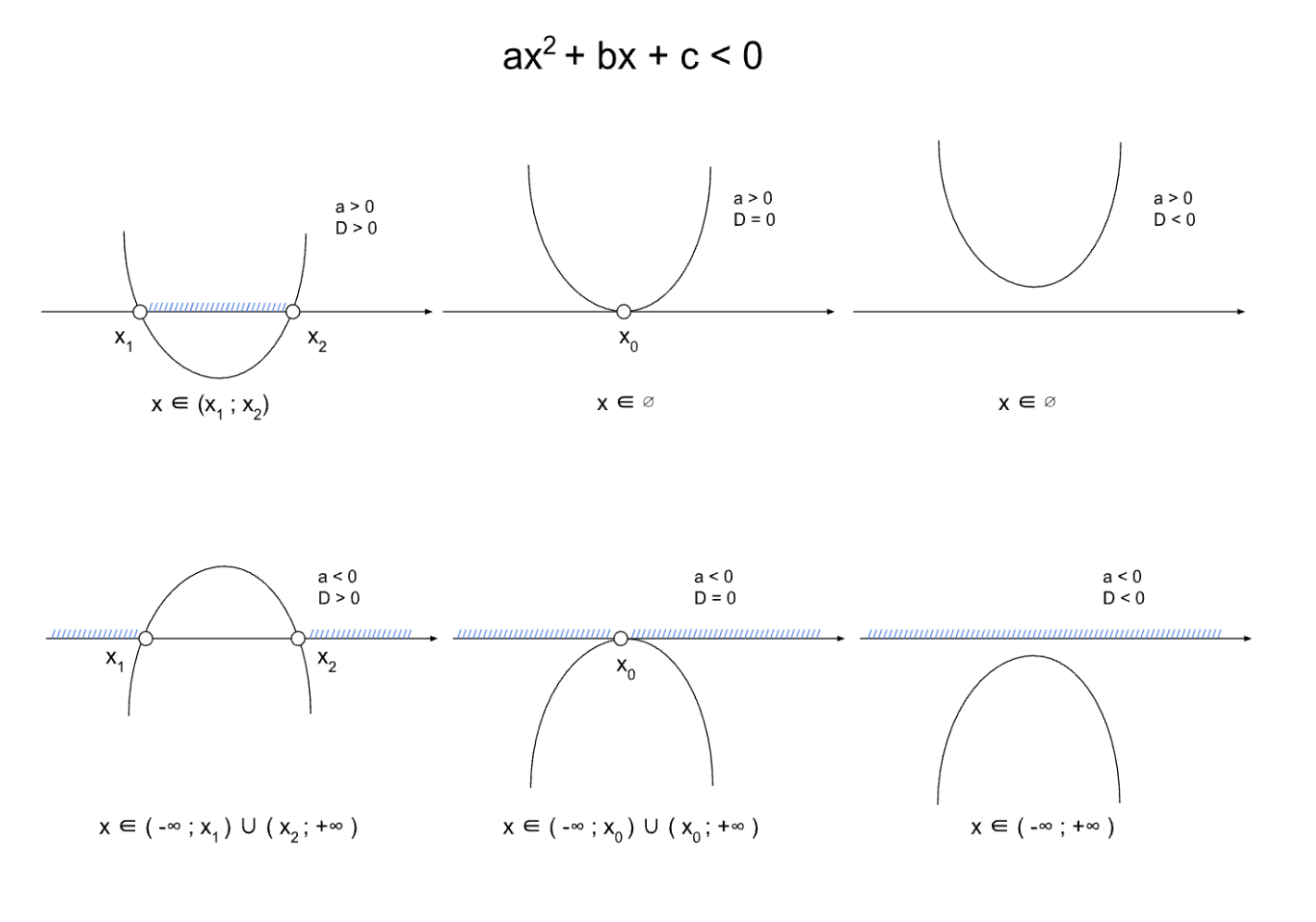
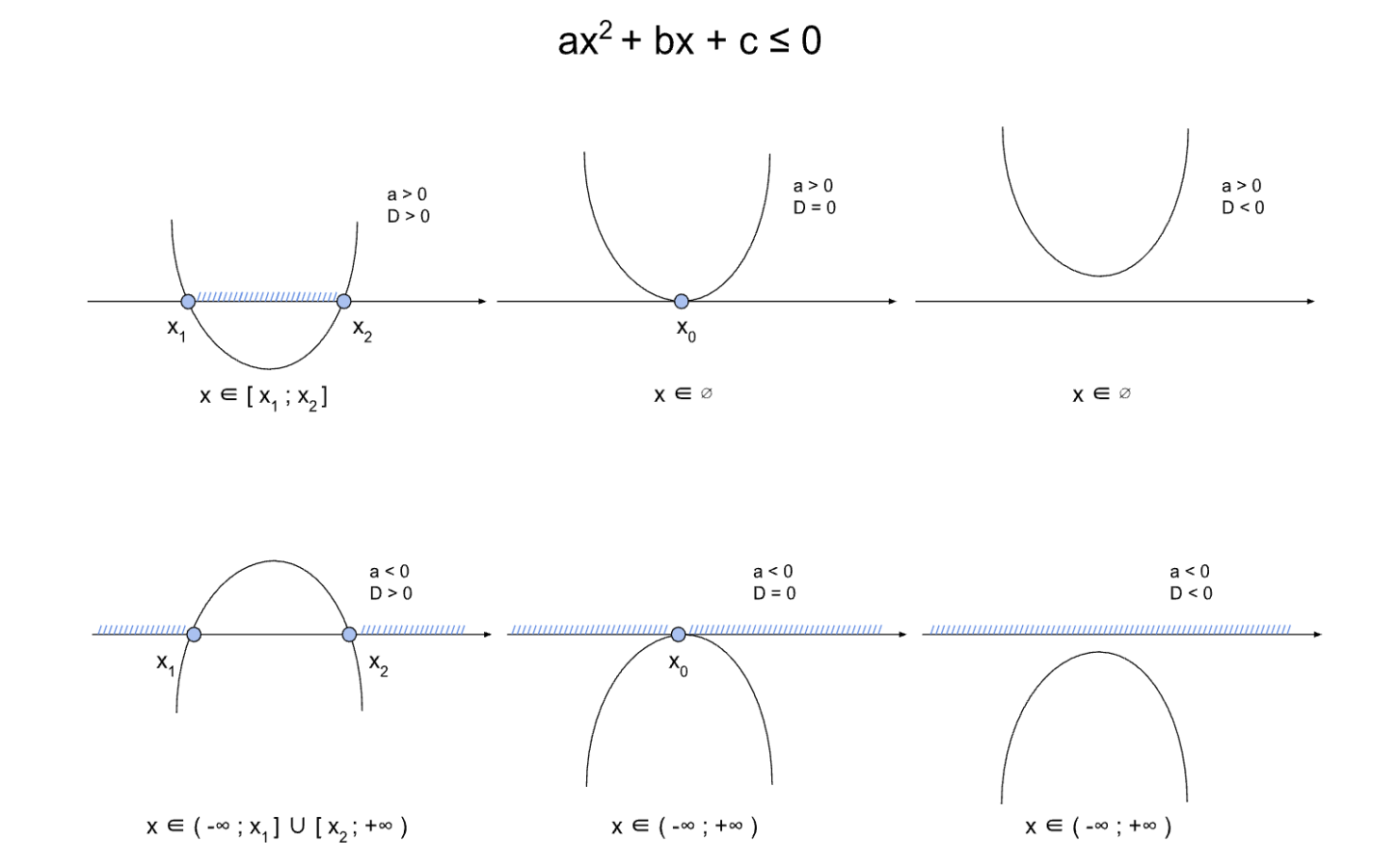
Примеры

Решим неравенство: 9x² + 3x — 2 > 0.

Коэффициент a = 9, a > 0, значит, ветви параболы направлены вверх. Приравниваем левую часть неравенства к нулю: 9x² + 3x — 2 = 0.

Находим дискриминант: D = 3² — 4 × 9 × (-2) = 9 + 72 = 81, D > 0.

Так как дискриминант положительный, уравнение имеет два корня, находим их:

x₁ = —²/₃
x₂ = ¹/₃

Изображаем параболу, ветви которой стремятся вверх. Парабола пересекает ось OX в двух точках.

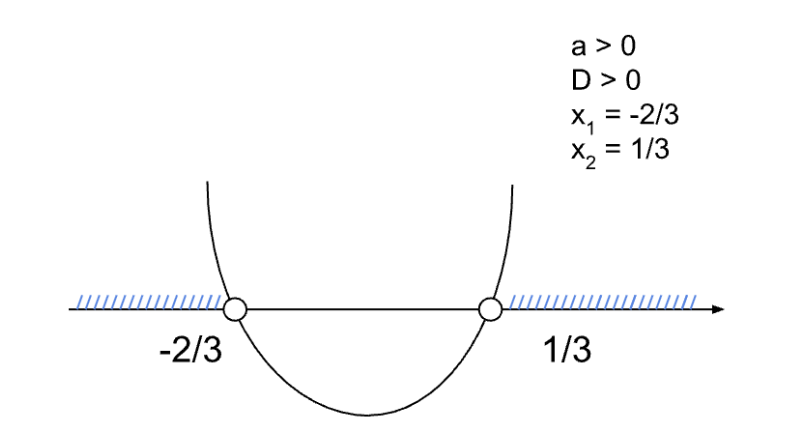
На рисунке видно, что решения, удовлетворяющие знаку неравенства > находятся в промежутках выше оси OX, а именно значения меньше x₁ и больше x₂ не включая границы: 

x ∈ (−∞; —²/₃) ∪ (¹/₃; +∞)

Ответ: x ∈ (−∞; —²/₃) ∪ (¹/₃; +∞)

Решим неравенство: 2x² + 4x + 3 < 0.

Коэффициент a = 2, a > 0, значит, ветви параболы направлены вверх. Приравниваем левую часть неравенства к нулю: 2x² + 4x + 3 = 0.

Находим дискриминант: D = 4² — 4 × 2 × 3 = 16 — 24 = -8, D < 0.

Так как дискриминант отрицательный, уравнение не имеет корней. 

Изображаем параболу, ветви которой стремятся вверх. Парабола не пересекает ось OX.

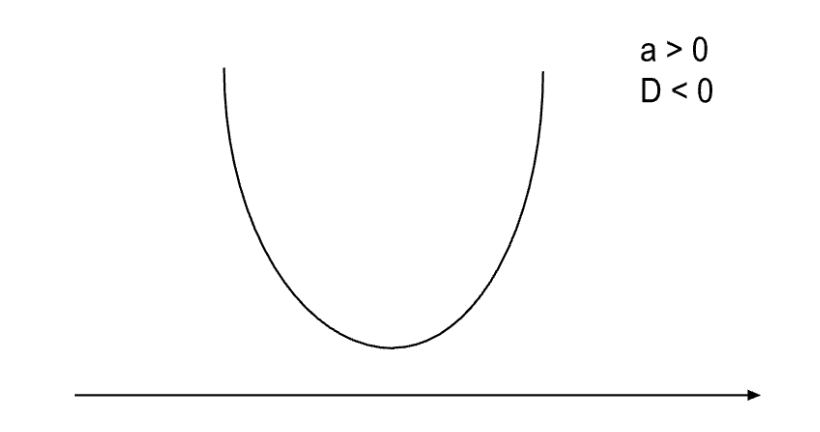
На рисунке видно, что нет подходящих решений для знака неравенства <:

x ∈ ∅

Ответ: x ∈ ∅

Решим неравенство: -x² + 4 ≥ 0.

Коэффициент a = -1, a < 0, значит, ветви параболы направлены вниз. Приравниваем левую часть неравенства к нулю: -x² + 4 = 0.

Находим дискриминант: D = 0² — 4 × (-1) × 4 = 0 + 16 = 16, D > 0.

Так как дискриминант положительный, уравнение имеет два корня, находим их:

x₁ = -2
x₂ = 2

Изображаем параболу, ветви которой стремятся вниз. Парабола пересекает ось OX в двух точках.

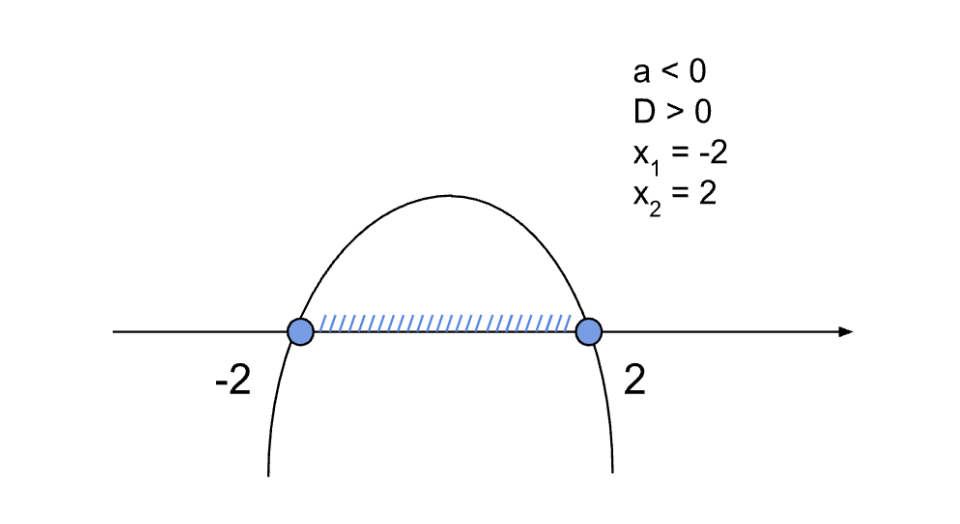
На рисунке видно, что решения, удовлетворяющие знаку неравенства ≥, находятся в промежутке выше оси OX, между точками x₁ и x₂ включая границы: 

x ∈  [−2; 2]

Ответ: x ∈  [−2; 2]

Решим неравенство: x² + 64 ≥ 0.

Коэффициент a = 1, a > 0, значит, ветви параболы направлены вверх. Приравниваем левую часть неравенства к нулю: x² + 64 = 0.

Находим дискриминант: D = 0² — 4 × 1 × 64 = 0 — 256 = -256, D < 0 .

Так как дискриминант отрицательный, уравнение не имеет корней. Изображаем параболу, ветви которой стремятся вверх. Парабола не пересекает ось OX.

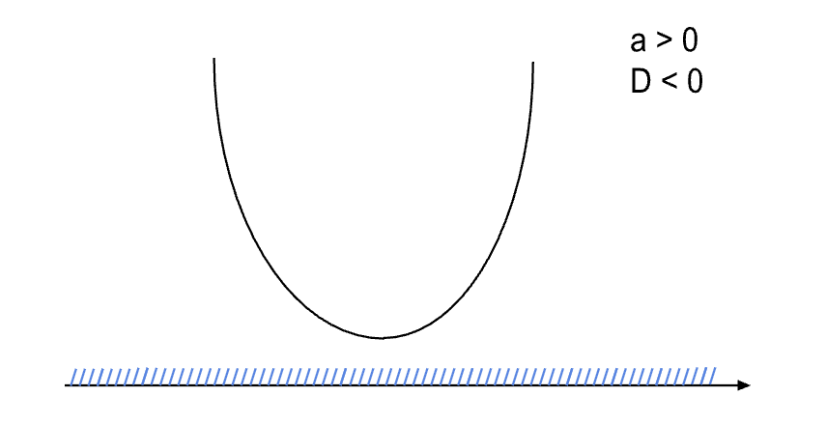
На рисунке видно, что все значения на числовой прямой удовлетворяют знаку неравенства ≥:
x ∈ R
Ответ: x ∈ (−∞; +∞)

Метод интервалов

Метод интервалов — это логическое продолжение анализа дискриминанта. После нахождения корней x₁ и x₂ мы исследуем знаки выражения на промежутках. Данный метод подходит для всех неравенств, у которых можно найти корни, то есть с неотрицательным дискриминантом. Но удобнее всего применять его к неравенствам, у которого левая часть разложена на множители.

Алгоритм:

1. Разложить квадратный трехчлен на множители, если неравенство представлено в стандартном виде при D ≥ 0. Для этого необходимо найти корни уравнения ax² + bx + c = 0 и представить неравенство в виде a(x — x₁)(x — x₂) > 0.
2. Отметить нули функции — корни уравнения, точки, в которых левая часть неравенства равна нулю, на числовой прямой.
3. Определить знаки выражения на каждом промежутке, подставляя тестовые точки.
4. Выбрать нужные промежутки согласно знаку неравенства.

Примеры

Решим неравенство: (x — 1)(x — 3) < 0.

Неравенство уже представлено в виде множителей, поэтому сразу определяем нули функции:

x₁ = 1
x₂ = 3

Отмечаем данные значения на числовой прямой, получили три промежутка: (−∞; 1), (1; 3), (3;+∞).

На первом промежутке возьмем, например, точку 0, подставим в левую часть неравенства: (0 — 1)(0 — 3) > 0, значит, знак +. На втором интервале можно взять точку 2, при подстановке получаем: (2 — 1)(2 — 3) < 0, знак -. И аналогично на третьем участке подставляем точку, например, 5: (5 — 1)(5 — 3) > 0, знак +. 

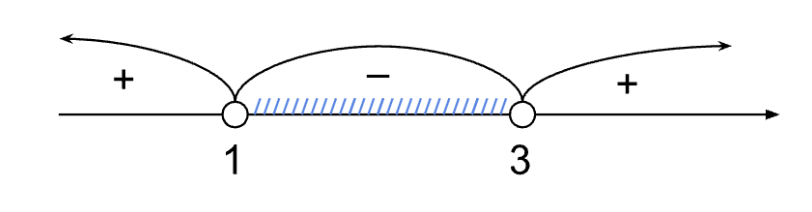
На рисунке видно, что знаку неравенства < удовлетворяет промежуток между x₁ и x₂ не включая границы: x ∈ (1; 3).

Ответ: x ∈ (1; 3)

Решим неравенство: 2x² — 7x — 4 ≥ 0.

Для разложения на множители квадратного трехчлена приравняем его к нулю и найдем корни полученного уравнения, если они есть: 2x² — 7x — 4 = 0. Для этого находим дискриминант: D = (-7)² — 4 × 2 × (-4) = 49 + 32 = 81, D > 0.

Так как дискриминант положительный, уравнение имеет два корня, находим их:

x₁ = –0,5
x₂ = 4

Таким образом, разложение квадратного трехчлена выглядит так:

2x² — 7x — 4 = 2(x + 0,5)(x — 4).

Полученные ранее корни являются нулями функции.

Отмечаем данные значения на числовой прямой — получили три промежутка: (−∞; –0,5], [–0,5; 4], [4;+∞).

На первом промежутке возьмем, например, точку -1, подставим в левую часть неравенства: 2(-1 + 0,5)(-1 — 4) > 0, значит, знак +. На втором интервале можно взять точку 2, при подстановке получаем: 2(2 + 0,5)(2 — 4) < 0, знак -. И аналогично на третьем участке подставляем точку, например, 5: 2(5 + 0,5)(5 — 4) > 0, знак +.

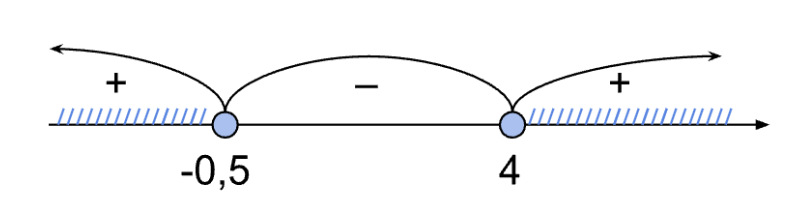
На рисунке видно, что знаку неравенства ≥ удовлетворяют два промежутка — меньше x₁ и больше x₂ включая границы: x ∈ (−∞; -0,5] ∪ [4; +∞).

Ответ: x ∈ (−∞; -0,5] ∪ [4; +∞)

Системы квадратных неравенств с одной переменной

Система квадратных неравенств — это два или более квадратных неравенств, объединенных фигурной скобкой. Решением системы будут все значения переменной, которые одновременно удовлетворяют каждому неравенству.

Алгоритм:

1. Решить каждое неравенство отдельно любым методом.
2. Изобразить решение всех неравенств на одной числовой прямой. 
3. Найти пересечение решений — общую область, где выполняются все неравенства системы одновременно. 

Примеры

Решим систему:

Решаем первое неравенство: x² — 4 ≤ 0 → x ∈ [−2; 2].

Решаем второе неравенство: 2x² — x — 1 > 0 → x ∈ (−∞; −0,5) ∪ (1; +∞).

Изображаем решения неравенств на числовой прямой:

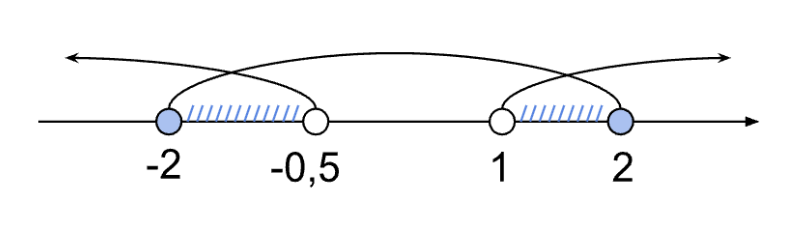
Находим пересечение x ∈ [−2; 2] и x ∈ (−∞; −0,5) ∪ (1; +∞). Общее решение: 

x ∈ [−2; −0,5) ∪ (1; 2].  

Ответ: x ∈ [−2; −0,5) ∪ (1; 2]

Решим систему:

Решаем первое неравенство: x² — 3x + 2 < 0 → x ∈ (1; 2).

Решаем второе неравенство: x² + x — 6 > 0 → x ∈ (−∞; −3) ∪ (2; +∞).

Изображаем решения неравенств на числовой прямой:

Ищем пересечение x ∈ (1; 2) и x ∈ (−∞; −3) ∪ (2; +∞). Общих точек нет:

x ∈ ∅

Ответ: x ∈ ∅

Решим систему: 

Решаем первое неравенство: x² — 4x + 4 ≤ 0 → x = 2.

Решаем второе неравенство: x² — 5x + 6 ≥ 0  → x ∈ (−∞; 2] ∪ [3; +∞).

Изображаем решения неравенств на числовой прямой:

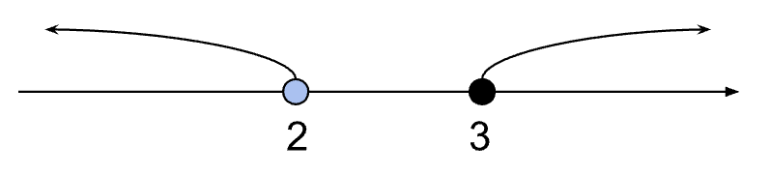
Ищем пересечение x = 2 и x ∈ (−∞; 2] ∪ [3; +∞). Общее решение — только одна точка: x = 2.

Ответ: x = 2

Системы неравенств могут содержать в себе различные неравенства: линейные, квадратные, дробно-рациональные, показательные и так далее. Поскольку мы уже освоили линейные неравенства, рассмотрим комбинированный пример, где одно неравенство — квадратное, а второе — линейное.

Решим систему:

Решаем первое неравенство: x² — 4x + 3 ≤ 0 → x ∈ [1; 3].

Решаем второе неравенство: 2x — 3 > 0  → x ∈ (1,5; +∞).

Изображаем решения неравенств на числовой прямой:

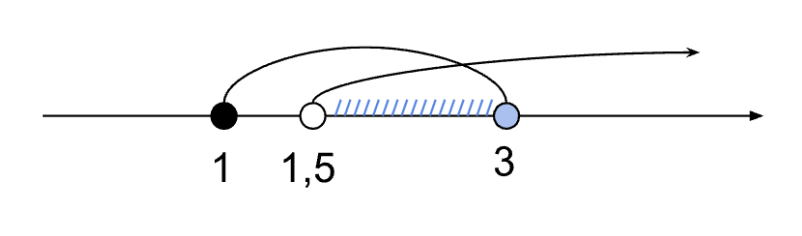
Ищем пересечение x ∈ [1; 3] и x ∈ (1,5; +∞). Общее решение: x ∈ (1.5; 3].

Ответ: x ∈ (1.5; 3]

Задачи по теме «Квадратные неравенства»

Ниже вы найдете подборку задач по теме. Совет: попробуйте решать каждую задачу разными методами — это поможет лучше понять тему и подготовиться к экзаменам.

Задача 1

Решите неравенство: x² − 5x + 6 > 0.

Задача 2

Решите неравенство: (x + 2)(x — 3) ≤ 0.

Задача 3

Решите систему:

Задача 4

Решите систему:

Ответы к задачам

Ниже приведены подробные решения задач. Если ваш ответ не совпал — не спешите смотреть решение, попробуйте найти ошибку самостоятельно.

Задача 1

Решим неравенство x² − 5x + 6 > 0 с помощью метода анализа дискриминанта и направления параболы.

Коэффициент a = 1, a > 0, значит, ветви параболы направлены вверх. Приравниваем левую часть неравенства к нулю: x² − 5x + 6= 0.

Находим дискриминант: D = (-5)² — 4 × 1 × 6 = 25 — 24 = 1, D > 0.

Так как дискриминант положительный, уравнение имеет два корня, находим их:

x₁ = 2
x₂ = 3

Парабола пересекает ось OX в двух точках, а ветви направлены вверх. Значит, решения, удовлетворяющие знаку неравенства >, находятся в промежутках выше оси OX, а именно значения меньше x₁ и больше x₂ не включая границы:

x ∈ (−∞; 2) ∪ (3; +∞).

Ответ: x ∈ (−∞; 2) ∪ (3; +∞)

Задача 2 

Решим неравенство (x + 2)(x — 3) ≤ 0 с помощью метода интервалов.

Неравенство уже представлено в виде множителей, поэтому сразу определяем нули функции:

x₁ = -2
x₂ = 3

Отмечаем данные значения на числовой прямой, получаем три промежутка: (−∞; -2], [-2; 3], [3;+∞). На первом промежутке возьмем, например, точку -3, подставим в левую часть неравенства: (-3 + 2)(-3 — 3) > 0, значит, знак +. На втором интервале можно взять точку 0, при подстановке получаем: (0 + 2)(0 — 3) < 0, знак -. И аналогично на третьем участке подставляем точку, например, 4: (4 + 2)(4 — 3) > 0, знак +. 

Значит, знаку неравенства ≤ удовлетворяет промежуток между x₁ и x₂ включая границы: x ∈ [−2; 3].

Ответ: x ∈ [−2; 3]

Задача 3

Решаем первое неравенство: x² — 4 ≤ 0 → x ∈ [−2; 2].

Решаем второе неравенство: 2x² — x — 1 > 0  → x ∈ (−∞; −0,5) ∪ (1; +∞).

Ищем пересечение x ∈ [−2; 2] и x ∈ (−∞; −0,5) ∪ (1; +∞). Общее решение: 

x ∈ [−2; −0,5) ∪ (1; 2].

Ответ: x ∈ [−2; −0,5) ∪ (1; 2]

Задача 4

Решаем первое неравенство: x² — 3x + 2 < 0 → x ∈ (1; 2).

Решаем второе неравенство: x + 1 ≥ 0  → x ∈ [-1; +∞).

Ищем пересечение x ∈ (1; 2) и x ∈ [-1; +∞). Общее решение: x ∈ (1; 2).

Ответ: x ∈ (1; 2)

Популярные вопросы и ответы

Отвечает Ольга Комарова, учитель математики: