Логарифмические неравенства
Научимся решать логарифмические неравенства, учитывая ОДЗ и основание логарифма. Пошагово разберем все методы с примерами и практическими задачами
Представьте, что вы пытаетесь узнать, за какое время ваши инвестиции удвоятся при определенной процентной ставке. Или вам нужно понять, как меняется громкость звука в децибелах или кислотность раствора. Все эти процессы описываются с помощью логарифмов, а чтобы их анализировать и делать прогнозы, необходимо уметь работать с логарифмическими неравенствами.
В отличие от других неравенств, здесь переменная находится под знаком логарифма — это накладывает особые ограничения и определяет специальные правила их решения.
Что такое логарифмические неравенства в алгебре
Логарифмическое неравенство — это неравенство, в котором неизвестная переменная содержится под знаком логарифма или в его основании.
В таких неравенствах всегда сравниваются:
- логарифмическая функция и число,
- две логарифмические функции.
Знаком сравнения может быть любой из символов: >, <, ≥, ≤.
Выделяют три основных вида логарифмических неравенств.
Простейшие логарифмические неравенства
Неравенства, где с одной стороны стоит логарифмическая функция, а с другой — число.
logaf(x) > b,
где:
- a — основание логарифма, положительное число, не равное единице (a > 0, a ≠ 1),
- f(x) —подлогарифмическое выражение, зависящее от переменной x (f(x) > 0),
- b — заданное число.
Область допустимых значений (ОДЗ): f(x) > 0
Пример: log2(x + 1) > 3
Стандартные логарифмические неравенства
Неравенства, где сравниваются два логарифма с равными основаниями или приводимые к равным:
logaf(x) > logag(x),
где:
- a — основание логарифма, положительное число, не равное единице (a > 0, a ≠ 1),
- f(x) и g(x) — подлогарифмические выражения, зависящие от переменной x (f(x) > 0, g(x) > 0).
ОДЗ: f(x) > 0, g(x) > 0
Пример: log7(2x) ≤ log7(x + 3)
Логарифмические неравенства с переменным основанием
Неравенства, где основание логарифма тоже зависит от переменной:
logh(x)f(x) > logh(x)g(x),
где:
- h(x) — основание логарифма, зависящее от x, положительное значение, не равное единице (h(x) > 0, h(x) ≠ 1),
- f(x) и g(x) — подлогарифмические выражения, зависящие от переменной x (f(x) > 0, g(x) > 0).
ОДЗ: f(x) > 0, g(x) > 0, h(x) > 0, h(x) ≠ 1
Пример: log(x-1)(3x) > 2
Полезная информация о логарифмических неравенствах
Поняв общую классификацию, полезно запомнить ключевые характеристики, которые определяют подход к решению. Эти свойства объясняют, почему методы решения работают именно так.
| Свойства и особенности логарифмических неравенств | Описание |
|---|---|
| Область определения (ОДЗ) | Подлогарифмическое выражение должно быть строго больше нуля: f(x) > 0. Основание логарифма положительно и не равно единице: a > 0, a ≠ 1 |
| Монотонность | При a > 1 функция возрастает, при 0 < a < 1 — убывает. Это определяет правило смены знака неравенства при отбрасывании логарифмов |
| Частые ошибки при решении | Неучет ОДЗ, неправильная смена знака при 0 < a < 1, применение преобразований, сужающих ОДЗ |
Что такое решение неравенства
Решить логарифмическое неравенство — значит найти все значения переменной x, при которых неравенство становится верным с учетом ОДЗ.
В отличие от логарифмических уравнений, которые часто имеют конечное число корней, решения логарифмических неравенств обычно представляют собой бесконечное множество значений — числовой промежуток или объединение нескольких промежутков.
Рассмотрим два примера:
- уравнение: log2x = 3 → x = 8
- неравенство: log2x > 3 → x ∈ (8; +∞)
Типы решений неравенств
Результат логарифмического неравенства может быть записан различными способами. Существует три основные формы записи решений.
1. Запись в виде неравенства. Является самым простым способом представить решение. Типы записи:
- x > a, x < a — строгий ответ
- x ≥ a, x ≤ a — нестрогий ответ
- a < x < b, a ≤ x ≤ b, a < x ≤ b, a ≤ x < b — двойное неравенство
Примеры:
log3(x — 1) < 2 → 1 < x < 10
log0,52x ≥ -1 → x > 0
2. Запись в виде числового промежутка. Является более формальной математической записью. Типы промежутков:
- (a; b) — интервал (a < x < b)
- (a; b] — полуинтервал (a < x ≤ b)
- [a; b) — полуинтервал (a ≤ x < b)
- [a; b] — отрезок (a ≤ x ≤ b)
- (-∞; a) — открытый луч (x < a)
- (a; +∞) — открытый луч (x > a)
- (-∞; a] — закрытый луч (x ≥ a)
- [a; +∞) — закрытый луч (x ≥ a)
Примеры:
lg(3x — 6) > 1 → x ∈ (4; +∞)
log2(7 — x) ≤ 2 → x ∈ [3; 7)
3. Графическое представление. Наглядный способ изображения решения на числовой прямой.
Правила обозначений:
- ● — точка включается (для знаков ≥ или ≤)
- ○ — точка не включается (для знаков > или <)
- → или ← — направление решения
Примеры:
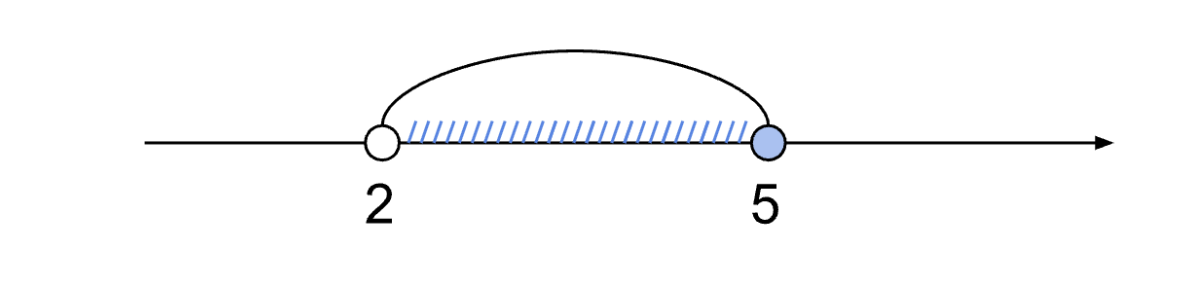
log4(x — 1) ≤ 1 → x ∈ (2; 5]
log0,5(x² — x — 6) < 0 → x ∈ (-∞; -2) ∪ (3; +∞)

Все три формы записи решений являются равнозначными и используются в зависимости от конкретной задачи или требований. В школьной практике часто требуется представлять решение всеми тремя способами.

Методы решения логарифмических неравенств
Для решения логарифмических неравенств используется три ключевых метода, выбор которых зависит от вида неравенства. Внимательно изучим каждый.
Классический метод для решения логарифмических неравенств
Данный метод является самым распространенным. Его также можно назвать методом сравнения аргументов логарифма или методом отбрасывания логарифмов. Подходит для простейших логарифмических неравенств, стандартных и с переменным основанием.
Для простейших неравенств вида logaf(x) > b (или <, ≥, ≤)
Алгоритм решения следующий:
1. Записать ОДЗ: f(x) > 0.
2. Представить число b в виде логарифма с основанием а: b = logaab.
3. Перейти к неравенству вида: logaf(x) > logaab.
4. Перейти к сравнению аргументов логарифмов, учитывая основание a.
Если a > 1, знак неравенства сохраняется:
logaf(x) > logaab ⇔ f(x) > ab
logaf(x) < logaab ⇔ f(x) < ab
Если 0 < a < 1, знак неравенства меняется на противоположный:
logaf(x) > logaab ⇔ f(x) < ab
logaf(x) < logaab ⇔ f(x) > ab
5. Решить полученное неравенство.
6. Найти пересечение полученного решения с ОДЗ.
Примеры
Решим неравенство: log2(3x — 1) > 5.
Находим ОДЗ: 3x — 1 > 0 → x ∈ (⅓; +∞).
Представим число 5 в виде логарифма с основанием 2 : 5 = log225 = log232.
Неравенство принимает вид: log2(3x — 1) > log232.
Основание 2 > 1, при переходе к сравнению аргументов знак сохраняется:
3x — 1 > 32 → x ∈ (11; +∞).
Накладываем на решение x ∈ (11; +∞) ОДЗ x ∈ (⅓; +∞). Получаем: x ∈ (11; +∞).
Ответ: x ∈ (11; +∞).
Решим неравенство: log0,2(4 — x) ≥ -2.
Находим ОДЗ: 4 — x > 0 → x ∈ (-∞; 4).
Представим число -2 в виде логарифма с основанием 0,2: -2 = log0,2(0,2)-2 = log0,225.
Неравенство принимает вид: log0,2(4 — x) ≥ log0,225.
Основание 0 < 0,2 < 1, при переходе к сравнению аргументов знак меняется:
4 — x ≤ 25 → x ∈ [-21; +∞).
Накладываем на решение x ∈ [-21; +∞) ОДЗ x ∈ (-∞; 4). Получаем: x ∈ [-21; 4).
Ответ: x ∈ [-21; 4)
Для стандартных логарифмических неравенств вида logaf(x) > logag(x) (или <, ≥, ≤)
Алгоритм решения:
1. Записать ОДЗ: f(x) > 0, g(x) > 0.
2. Перейти к сравнению аргументов логарифмов, учитывая основание a.
Если a > 1, знак неравенства сохраняется:
logaf(x) > logag(x) ⇔ f(x) > g(x)
logaf(x) < logag(x) ⇔ f(x) < g(x)
Если 0 < a < 1, знак неравенства меняется на противоположный:
logaf(x) > logag(x) ⇔ f(x) < g(x)
logaf(x) < logag(x) ⇔ f(x) > g(x)
3. Решить полученное неравенство.
4. Найти пересечение полученного решения с ОДЗ.
Примеры
Решим неравенство: log3(x + 5) < log3(1 — x).
Находим ОДЗ:
x + 5 > 0 → x ∈ (-5; +∞)
1 — x > 0 → x ∈ (-∞; 1)
Пересечение ОДЗ: x ∈ (-5; 1).
Основание 3 > 1, при переходе к сравнению аргументов знак сохраняется:
x + 5 < 1 — x → x ∈ (-∞; -2).
Накладываем на решение x ∈ (-∞; -2) ОДЗ x ∈ (-5; 1). Получаем: x ∈ (-5; -2).
Ответ: x ∈ (-5; -2)
Решим неравенство: log0,5(x2) ≥ log0,5(3x + 4).
Находим ОДЗ:
x2 > 0 → x ∈ (-∞; 0) ∪ (0; +∞)
3x + 4 > 0 → x ∈ (-1⅓; +∞)
Пересечение ОДЗ: x ∈ (-1⅓; 0) ∪ (0; +∞).
Основание 0 < 0,5 < 1, при переходе к сравнению аргументов знак меняется:
x2 ≤ 3x + 4 → x² — 3x — 4 ≤ 0 → x ∈ [-1; 4].
Накладываем на решение x ∈ [-1; 4] ОДЗ x ∈ (-1⅓; 0) ∪ (0; +∞). Получаем:
x ∈ [-1; 0) ∪ (0; 4].
Ответ: x ∈ [-1; 0) ∪ (0; 4]
Для логарифмических неравенств с переменным основанием вида logh(x)f(x) > logh(x)g(x) (или <, ≥, ≤)
В данном случае основание h(x) может быть как больше 1, так и находиться между 0 и 1. Поэтому мы должны рассмотреть оба случая, а затем объединить их решения.
Алгоритм решения:
1. Записать ОДЗ: f(x) > 0, g(x) > 0, h(x) > 0, h(x) ≠ 1.
2. Рассмотреть два случая в зависимости от основания h(x).
При h(x) > 1 знак неравенства сохраняется:
logh(x)f(x) > logh(x)g(x) ⇔
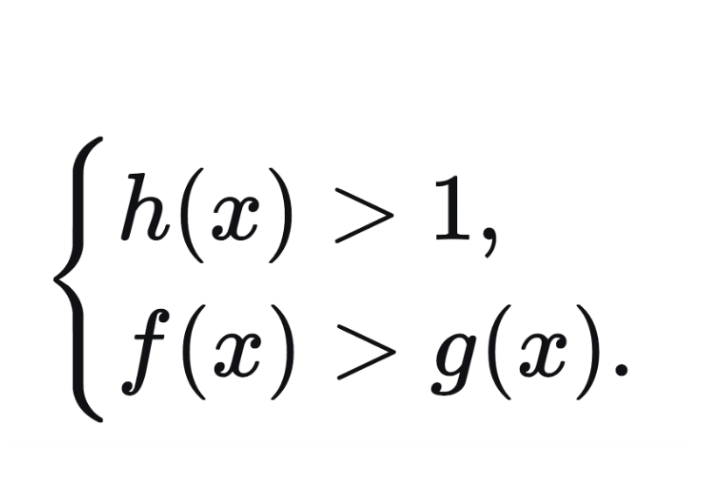
logh(x)f(x) < logh(x)g(x) ⇔
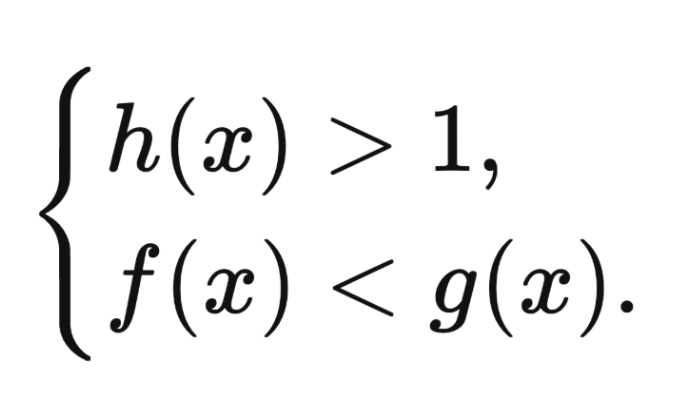
При 0 < h(x) < 1 знак неравенства меняется на противоположный:
logh(x)f(x) > logh(x)g(x) ⇔
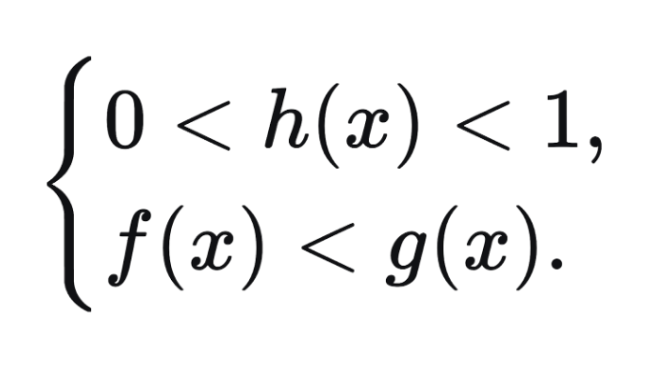
logh(x)f(x) < logh(x)g(x) ⇔
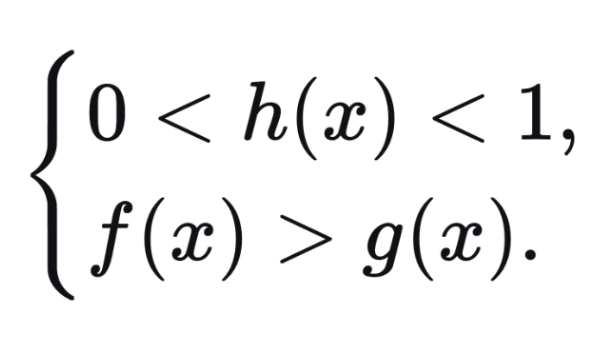
3. Решить каждую систему отдельно.
4. Объединить решения, полученные в обоих случаях, и найти пересечение с ОДЗ.
Примеры
Решим неравенство: logx(2x — 3) > logx(x + 1).
Находим ОДЗ:
2x — 3 > 0 → x ∈ (1,5; +∞)
x + 1 > 0 → x ∈ (-1; +∞)
x > 0 → x ∈ (0; +∞)
x ≠ 1 → x ∈ (-∞; 1) ∪ (1; +∞)
Пересечение ОДЗ: x ∈ (1,5; +∞).
Рассматриваем два случая:
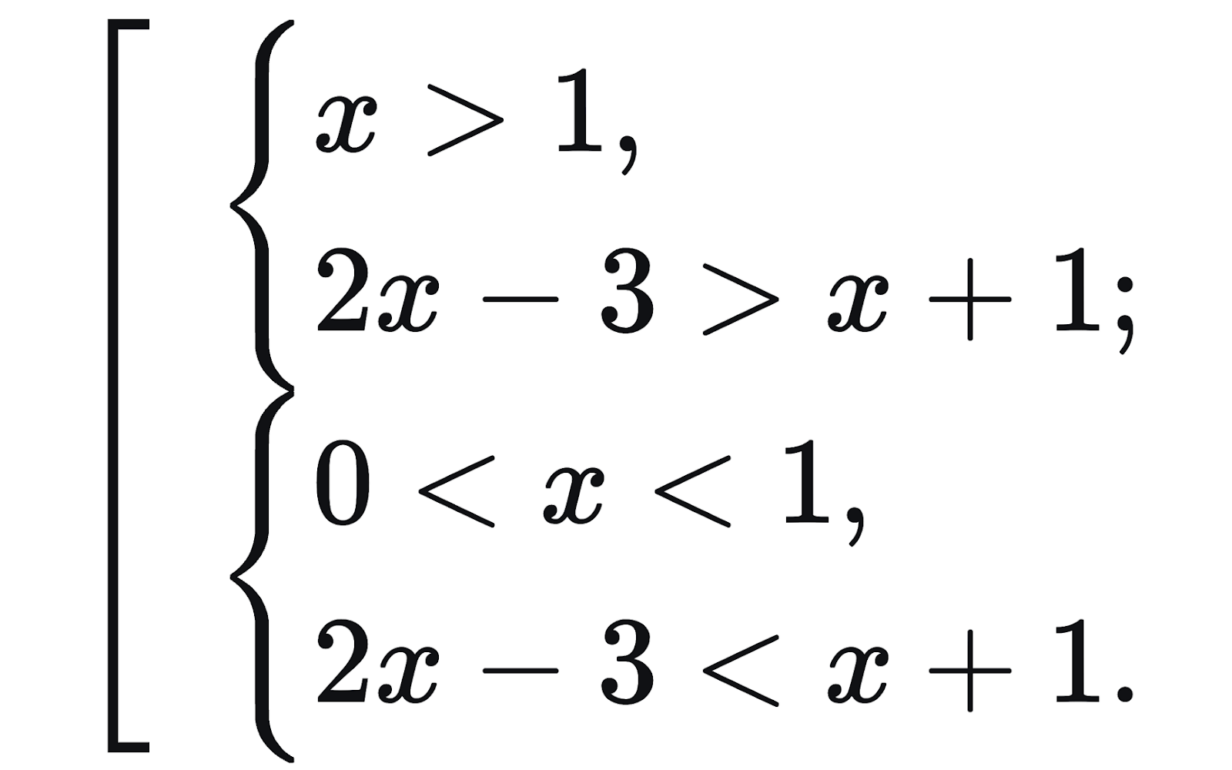
Решение первой системы: x ∈ (4; +∞).
Решение второй системы: x ∈ (0; 1).
Объединяем решения, полученные в обоих случаях: x ∈ (0; 1) ∪ (4; +∞).
Накладываем на решение x ∈ (0; 1) ∪ (4; +∞) ОДЗ x ∈ (1,5; +∞). Получаем: x ∈ (4; +∞).
Ответ: x ∈ (4; +∞)
Метод рационализации для решения логарифмических неравенств
Этот метод помогает упростить сложные логарифмические неравенства. Он позволяет заменить разность логарифмов на разность их аргументов, умноженную на выражение, зависящее от основания, что сводит задачу к решению алгебраического неравенства. Особенно эффективен для неравенств с переменным основанием.
Для стандартных логарифмических неравенств вида logaf(x) > logag(x) (или <, ≥, ≤)
Придерживайтесь этого алгоритма решения.
- Записать ОДЗ: f(x) > 0, g(x) > 0.
- Перенести все слагаемые в одну сторону: logaf(x) — logag(x) > 0.
- Применить формулу рационализации:
logaf(x) — logag(x) > 0 ⇔ (a — 1)(f(x) — g(x)) > 0 - Решить полученное алгебраическое неравенство.
- Найти пересечение полученного решения с ОДЗ.
Примеры
Решим неравенство: log3(x + 1) ≥ log3(2x — 5).
Находим ОДЗ:
x + 1 > 0 → x ∈ (-1; +∞)
2x — 5 > 0 → x ∈ (2,5; +∞)
Пересечение ОДЗ: x ∈ (2,5; +∞).
Переносим все слагаемые в одну сторону: log3(x + 1) — log3(2x — 5) ≥ 0.
Применяем формулу рационализации:
(3 — 1)((x + 1) — (2x — 5)) ≥ 0 → 2(-x + 6) ≥ 0 → -x + 6 ≥ 0 → x ∈ (-∞; 6].
Накладываем на решение x ∈ (-∞; 6] ОДЗ x ∈ (2,5; +∞). Получаем: x ∈ (2,5; 6].
Ответ: x ∈ (2,5; 6]
Решим неравенство: log1/2(4x) < log1/2(x + 3).
Находим ОДЗ:
4x > 0 → x ∈ (0; +∞)
x + 3 > 0 → x ∈ (-3; +∞)
Пересечение ОДЗ: x ∈ (0; +∞).
Переносим все слагаемые в одну сторону: log1/2(4x) — log1/2(x + 3) < 0.
Применяем формулу рационализации:
(½ — 1)(4x — (x + 3)) < 0 → -½(3x — 3) < 0 → 3x — 3 > 0 → x ∈ (1; +∞).
Накладываем на решение x ∈ (1; +∞) ОДЗ x ∈ (0; +∞). Получаем: x ∈ (1; +∞).
Ответ: x ∈ (1; +∞)
Для логарифмических неравенств с переменным основанием вида logh(x)f(x) > logh(x)g(x) (или <, ≥, ≤)
Алгоритм решения:
- Записать ОДЗ: f(x) > 0, g(x) > 0, h(x) > 0, h(x) ≠ 1.
- Перенести все слагаемые в одну сторону: logh(x)f(x) — logh(x)g(x) > 0.
- Применить формулу рационализации:
logh(x)f(x) — logh(x)g(x) > 0 ⇔ (h(x) — 1)(f(x) — g(x)) > 0 - Решить полученное алгебраическое неравенство.
- Найти пересечение полученного решения с ОДЗ.
Примеры
Решим неравенство: log(x + 1)(x + 3) > log(x + 1)(2x — 1).
Находим ОДЗ:
x + 3 > 0 → x ∈ (-3; +∞)
2x — 1 > 0 → x ∈ (0,5; +∞)
x + 1 > 0 → x ∈ (-1; +∞)
x + 1 ≠ 1 → x ∈ (-∞; 0) ∪ (0; +∞)
Пересечение ОДЗ: x ∈ (0,5; +∞).
Переносим все слагаемые в одну сторону: log(x + 1)(x + 3) — log(x + 1)(2x — 1) > 0.
Применяем формулу рационализации:
((x + 1) — 1)((x + 3) — (2x — 1)) > 0 → x(-x + 4) > 0 → x ∈ (0; 4).
Накладываем на решение x ∈ (0; 4) ОДЗ x ∈ (0,5; +∞). Получаем: x ∈ (0,5; 4).
Ответ: x ∈ (0,5; 4)
Решим неравенство: log(x — 2)5 > 1.
Находим ОДЗ:
x — 2 > 0 → x ∈ (2; +∞)
x — 2 ≠ 1 → x ∈ (-∞; 3) ∪ (3; +∞)
Пересечение ОДЗ: x ∈ (2; 3) ∪ (3; +∞).
Представим число 1 в виде логарифма: 1 = log(x — 2)(x — 2).
Переносим все слагаемые в одну сторону: log(x — 2)5 — log(x — 2)(x — 2) > 0.
Применяем формулу рационализации:
((x — 2) — 1)(5 — (x — 2)) > 0 → (x — 3)(7 — x) > 0 → x ∈ (3; 7).
Накладываем на решение x ∈ (3; 7) ОДЗ x ∈ (2; 3) ∪ (3; +∞). Получаем: x ∈ (3; 7).
Ответ: x ∈ (3; 7)
Метод замены для решения логарифмических неравенств
Этот метод является универсальным приемом для упрощения сложных логарифмических неравенств, которые сводятся к алгебраическим, чаще всего квадратным. Данный способ работает для тех неравенств, в которых можно выделить повторяющееся выражение logaf(x) или logh(x)f(x).
Для логарифмических неравенств с повторяющимся выражением logaf(x) или logh(x)f(x)
Алгоритм решения:
- Записать ОДЗ неравенства.
- Ввести новую переменную t = logaf(x) или t = logh(x)f(x).
- Подставить t в исходное неравенство. Получится алгебраическое неравенство относительно t.
- Решить это неравенство относительно t.
- Вернуться к исходной переменной, решив простейшее логарифмическое неравенство или логарифмическое неравенство с переменным основанием относительно x.
- Найти пересечение полученного решения с ОДЗ.
Примеры
Решим неравенство: log22(x + 2) — 4log2(x + 2) + 3 < 0.
Находим ОДЗ:
x + 2 > 0 → x ∈ (-2; +∞).
Делаем замену: t = log2(x + 2).
Получаем: t2 — 4t + 3 < 0 → t ∈ (1; 3).
Выполним обратную замену и решим два логарифмических неравенства с помощью способов, о которых говорили ранее:
log2(x + 2) > 1 → x ∈ (0; +∞)
log2(x + 2) < 3 → x ∈ (-∞; 6)
Общее пересечение решений: x ∈ (0; 6).
Накладываем на решение x ∈ (0; 6) ОДЗ x ∈ (-2; +∞). Получаем: x ∈ (0; 6).
Ответ: x ∈ (0; 6)
Решим неравенство: log2x2x — 3logx2x + 2 ≤ 0.
Находим ОДЗ:
x > 0 → x ∈ (0; +∞)
x ≠ 1 → x ∈ (-∞; 1) ∪ (1; +∞)
2x > 0 → x ∈ (0; +∞)
Пересечение ОДЗ: x ∈ (0; 1) ∪ (1; +∞).
Делаем замену: t = logx2x.
Получаем: t2 — 3t + 2 ≤ 0 → t ∈ [1; 2].
Выполним обратную замену и решим два логарифмических неравенства с помощью способов, о которых говорили ранее:
logx2x ≥ 1 → x ∈ (1; +∞)
logx2x ≤ 2 → x ∈ (0; 1) ∪ [2; +∞)
Общее пересечение решений: x ∈ [2; +∞).
Накладываем на решение x ∈ [2; +∞) ОДЗ x ∈ (0; 1) ∪ (1; +∞). Получаем: x ∈ [2; +∞).
Ответ: x ∈ [2; +∞)
Системы логарифмических неравенств

Системы логарифмических неравенств — это набор из двух или более неравенств, которые должны выполняться одновременно для одних и тех же значений переменной. Система может содержать только однотипные неравенства — логарифмические, и разнотипные — сочетать логарифмические неравенства с линейными, квадратными, дробно-рациональными, показательными и другими типами неравенств.
Алгоритм решения:
- Решить каждое неравенство системы в отдельности.
- Изобразить решение всех неравенств на одной числовой прямой.
- Найти пересечение этих решений — область, которая удовлетворяет всем неравенствам одновременно.
Примеры
Решим систему неравенств:
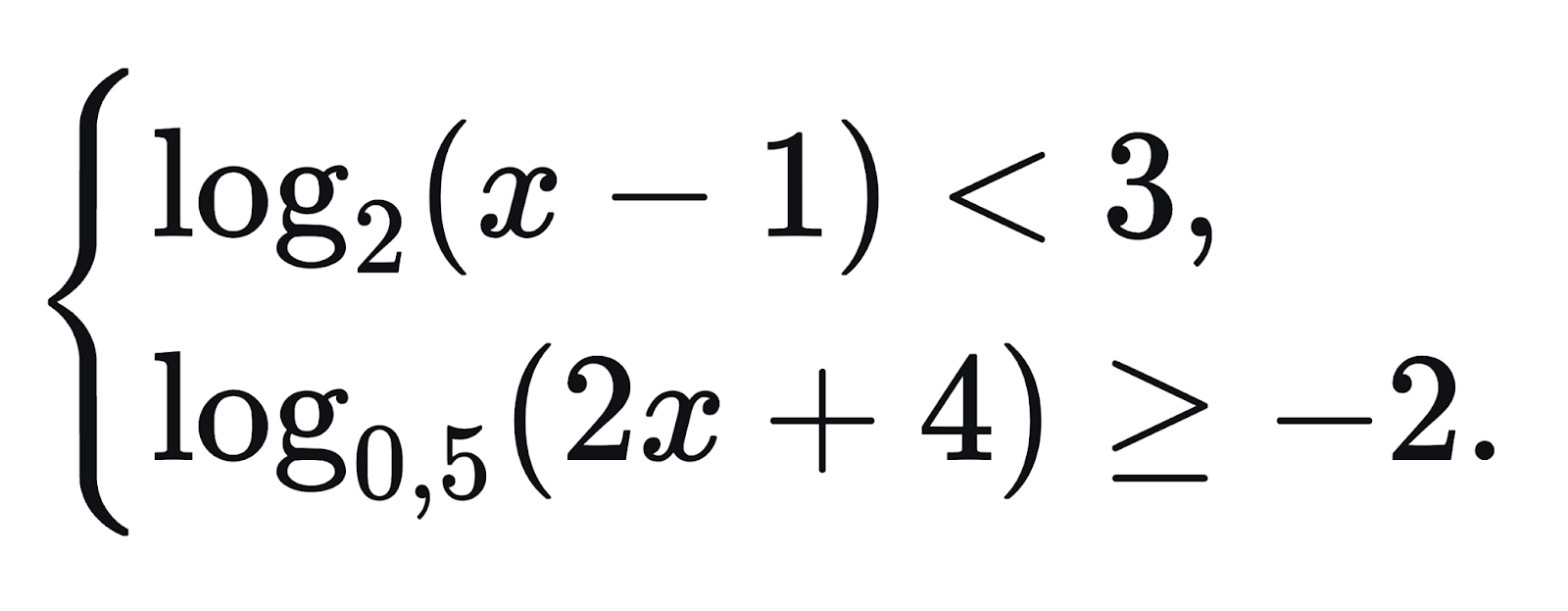
Решаем первое неравенство: log2(x — 1) < 3 → x ∈ (1; 9).
Решаем второе неравенство: log0,5(2x + 4) ≥ -2 → x ∈ (-2; 0].
Изображаем решения неравенств на числовой прямой:
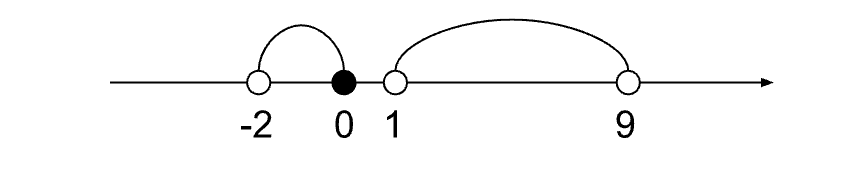
Находим пересечение x ∈ (1; 9) и x ∈ (-2; 0]. Общих решений нет.
Ответ: x ∈ ∅
Решим систему неравенств:
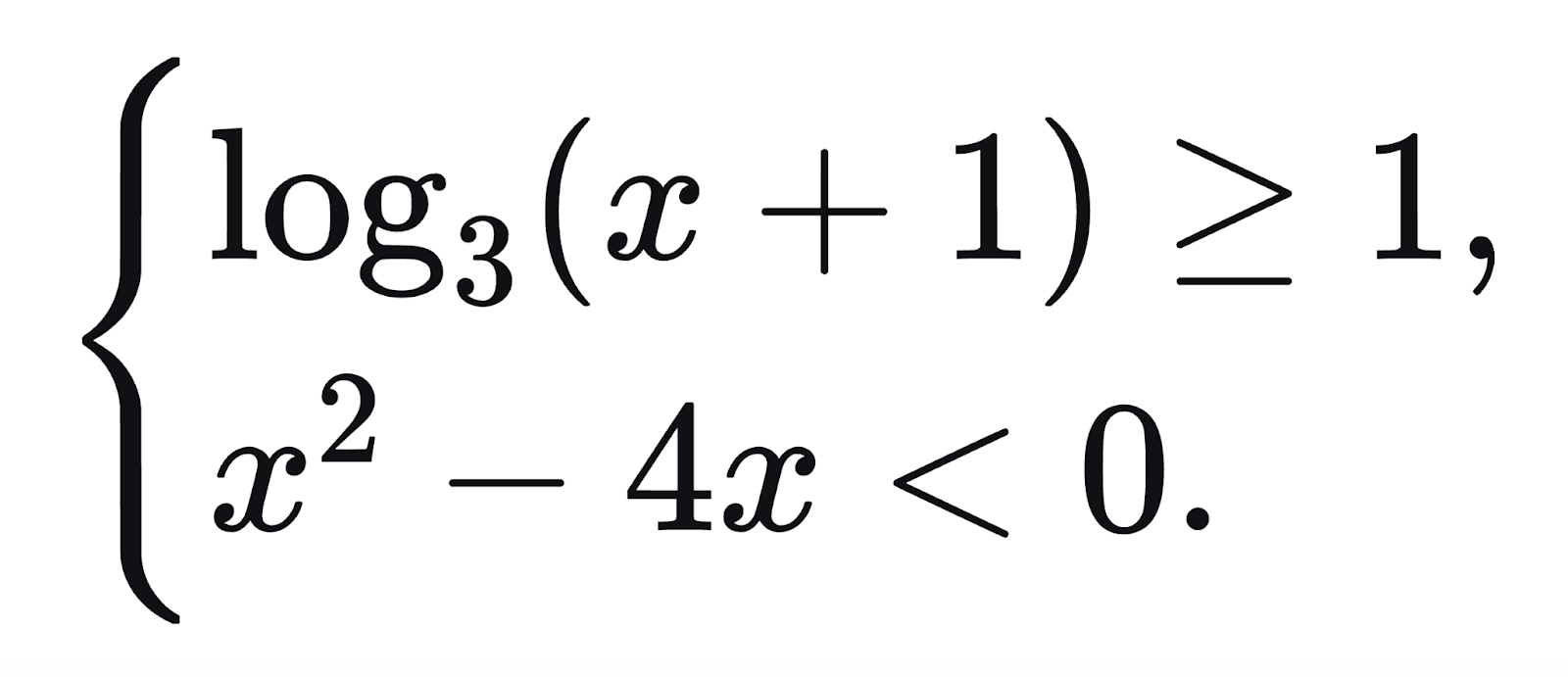
Решаем первое неравенство: log3(x + 1) ≥ 1 → x ∈ [2; +∞).
Решаем второе неравенство: x2 — 4x < 0 → x ∈ (0; 4).
Изображаем решения неравенств на числовой прямой:
Изображение: Ирина Соколова
Находим пересечение x ∈ [2; +∞) и x ∈ (0; 4). Общие решение: x ∈ [2; 4).
Ответ: x ∈ [2; 4)
Задачи по теме «Логарифмические неравенства»
Закрепите изученные методы на практике. Попробуйте решить эти задачи, подобрав для каждой подходящий способ решения. Не забывайте про ОДЗ и правило смены знака в зависимости от основания логарифма.
Задача 1
Решите неравенство: log4(2x — 6) > 2.
Решение и ответ к задаче 1
Находим ОДЗ: 2x — 6 > 0 → x ∈ (3; +∞).
Представим число 2 в виде логарифма с основанием 4: 2 = log442 = log416.
Неравенство принимает вид: log4(2x — 6) > log416.
Основание 4 > 1, при переходе к сравнению аргументов знак сохраняется:
2x — 6 > 16 → x ∈ (11; +∞).
Накладываем на решение x ∈ (11; +∞) ОДЗ x ∈ (3; +∞). Получаем: x ∈ (11; +∞).
Ответ: x ∈ (11; +∞)
Задача 2
Решите неравенство: log0,3(x + 4) ≤ log0,3(5x — 2).
Решение и ответ к задаче 2
Находим ОДЗ:
x + 4 > 0 → x ∈ (-4; +∞)
5x — 2 > 0 → x ∈ (0,4; +∞)
Пересечение ОДЗ: x ∈ (0,4; +∞).
Основание 0 < 0,3 < 1, при переходе к сравнению аргументов знак меняется:
x + 4 ≤ 5x — 2 → x ∈ (-∞; 1,5].
Накладываем на решение x ∈ (-∞; 1,5] ОДЗ x ∈ (0,4; +∞). Получаем: x ∈ (0,4; 1,5].
Ответ: x ∈ (0,4; 1,5]
Задача 3
Решите неравенство: log23x — 5log3x + 6 > 0.
Решение и ответ к задаче 3
Находим ОДЗ: x > 0 → x ∈ (0; +∞).
Делаем замену: t = log3x.
Получаем: t2 — 5t + 6 > 0 → t ∈ (-∞; 2) ∪ (3; +∞).
Выполним обратную замену и решим два логарифмических неравенства с помощью способов, о которых говорили ранее:
log3x > 3 → x ∈ (27; +∞)
log3x < 2 → x ∈ (-∞; 9)
Общее решение: x ∈ (-∞; 9) ∪ (27; +∞).
Накладываем на решение x ∈ (-∞; 9) ∪ (27; +∞) ОДЗ x ∈ (0; +∞). Получаем: x ∈ (0; 9) ∪ (27; +∞).
Ответ: x ∈ (0; 9) ∪ (27; +∞)
Задача 4
Решите неравенство: log(x — 1)(x + 2) > 1.
Решение и ответ к задаче 4
Находим ОДЗ:
x + 2 > 0 → x ∈ (-2; +∞)
x — 1 > 0 → x ∈ (1; +∞)
x — 1 ≠ 1 → x ∈ (-∞; 2) ∪ (2; +∞)
Пересечение ОДЗ: x ∈ (1; 2) ∪ (2; +∞).
Представим число 1 в виде логарифма: 1 = log(x — 1)(x — 1).
Переносим все слагаемые в одну сторону: log(x — 1)(x + 2) — log(x — 1)(x — 1) > 0.
Применяем формулу рационализации:
((x — 1) — 1)((x + 2) — (x — 1)) > 0 → x — 2 > 0 → x ∈ (2; +∞).
Накладываем на решение x ∈ (2; +∞) ОДЗ x ∈ (1; 2) ∪ (2; +∞). Получаем: x ∈ (2; +∞).
Ответ: x ∈ (2; +∞)
Задача 5
Решите систему неравенств:
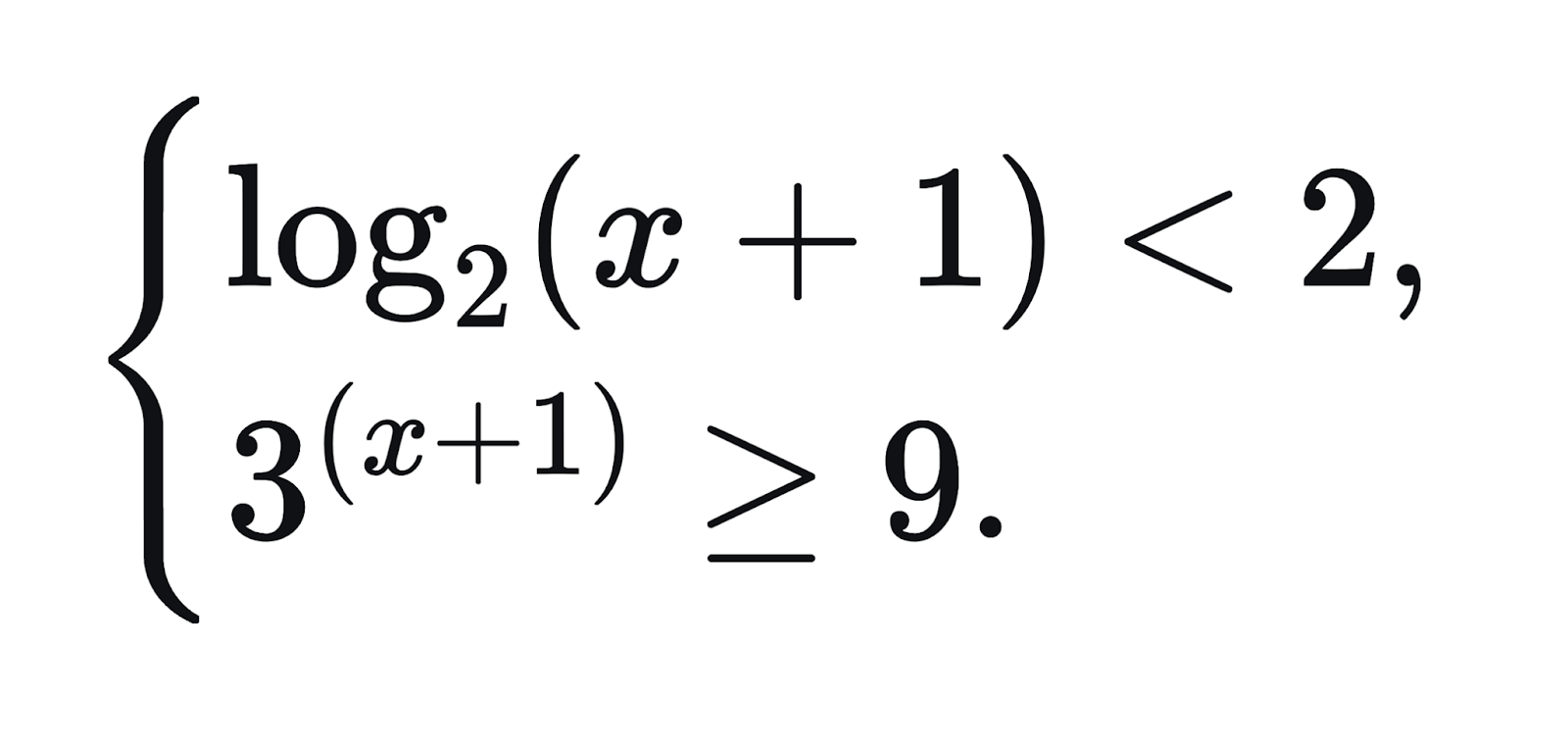
Решение и ответ к задаче 5
Решаем первое неравенство: log2(x + 1) < 2 → x ∈ (-1; 3).
Решаем второе неравенство: 3(x + 1) ≥ 9 → x ∈ [1; +∞).
Изображаем решения неравенств на числовой прямой:
Изображение: Ирина Соколова
Находим пересечение x ∈ (-1; 3) и x ∈ [1; +∞). Общее решение: x ∈ [1; 3).
Ответ: x ∈ [1; 3)
Популярные вопросы и ответы
Отвечает Ольга Комарова, учитель математики:
Почему логарифмические и показательные неравенства связаны между собой?
Поэтому при решении логарифмических неравенств мы всегда опираемся на свойства показательных функций: где они возрастают, где убывают, как ведут себя при разных основаниях. Знак в логарифмическом неравенстве меняется именно так же, как в показательных — все зависит от того, больше или меньше единицы основание. Эта связь очень важна.
Почему тему по алгебре «Логарифмические неравенства» изучают в 10-11 классах?
В 10–11 классе ученик готов воспринимать математику глубже: видеть не только «ответ в числах», но и рассуждать, анализировать условия, учитывать исключения. Логарифмические неравенства — это отличный тренажер для математического мышления.
В каких заданиях ЕГЭ по математике понадобится умение решать логарифмические неравенства?
В базовом ЕГЭ логарифмы не рассматриваются, так что эта тема целиком принадлежит профильному уровню. Но важно понимать: это не «узкая» тема, а естественное продолжение степеней и показателей, без которого картину школьной алгебры нельзя считать завершенной.









