Наибольший общий делитель (НОД)
Разберемся, что такое наибольший общий делитель, зачем он нужен и как его легко найти разными способами. Научимся применять НОД для решения практических задач
Простые числа — это кирпичики мира математики, а наибольший общий делитель — настоящий архитектор, который помогает находить общее в, казалось бы, разных числах.
Сокращение дробей, решение уравнений, оптимизация расчетов — везде используется работа с НОД. Его понимание не только упрощает вычисления, но и развивает логическое мышление, позволяя увидеть скрытую гармонию между числами. В статье мы разберем, что такое НОД, изучим эффективные алгоритмы его нахождения и закрепим знания на практических примерах.
Что такое наибольший общий делитель в математике
Наибольший общий делитель (НОД) двух или более натуральных чисел — это наибольшее натуральное число, на которое все исходные числа делятся без остатка.
Проще говоря, это самое большое число, которое является делителем для каждого из данных чисел.
Например, рассмотрим числа 12 и 18.
- Делители 12: 1, 2, 3, 4, 6, 12.
- Делители 18: 1, 2, 3, 6, 9, 18.
Общие делители для 12 и 18 — это 1, 2, 3, 6. Наибольший из них — 6. Значит, НОД(12, 18) = 6.
Полезная информация о наибольшем общем делителе
Понятие НОД тесно связано с другими фундаментальными идеями в математике. В таблице ниже собраны ключевые свойства и характеристики, которые помогут лучше ориентироваться в теме.
| Факт о наибольшем общем делителе | Описание |
|---|---|
| Основное свойство НОД | Наибольшее натуральное число, на которое делятся без остатка все исходные числа |
| НОД взаимно простых чисел | Если НОД двух или более чисел равен 1, такие числа называются взаимно простыми. Например, 8 и 15 |
| Связь НОД с НОК | Произведение НОД и НОК двух чисел равно произведению самих чисел: a × b = НОД (a; b) × НОК (a; b) |
| НОД любого числа с нулем | НОД любого числа a и нуля равен модулю этого числа: НОД (a; 0) = |a| |
| Свойство делимости | Если одно число делится на другое, то их НОД равен меньшему из чисел |
Алгоритмы нахождения НОД
Существует несколько надежных способов нахождения наибольшего общего делителя. Разберем два самых популярных и эффективных алгоритма.
С помощью разложения на простые множители
Этот метод основан на фундаментальной теореме арифметики, которая гласит: любое число можно разложить на простые множители.
Алгоритм:
- Разложить каждое число на простые множители.
- Выписать все общие простые множители, присутствующие в разложениях каждого числа.
- Возвести каждый общий множитель в наименьшую степень, с которой он входит в разложения.
- Перемножить полученные степени, НОД равен результату.
Примеры
Найдем НОД(84; 90).
Разложим на множители:
84 = 22 × 3 × 7
90 = 2 × 32 × 5
Общие простые множители: 2 и 3.
Выбираем наименьшие степени: 21 и 31.
НОД(84; 90) = 2 × 3 = 6.
Ответ: НОД(84; 90) = 6
Найдем НОД(200; 450; 600).
Разложим на множители:
200 = 23 × 52
450 = 2 × 32 × 52
600 = 23 × 3 × 52
Общие простые множители для всех трех чисел: 2 и 5.
Выбираем наименьшие степени: 21 и 52.
НОД(200; 450; 600) = 2 × 25 = 50.
Ответ: НОД(200; 450; 600) = 50
это интересно
С помощью алгоритма Евклида
Этот древний алгоритм особенно удобен для больших чисел, так как не требует длительного разложения их на множители. Он основан на следующем свойстве: НОД(a; b) = НОД(b; r), где r — остаток от деления a на b.
Алгоритм:
- Разделить большее число на меньшее.
- Если остаток от деления равен нулю, то меньшее число и есть НОД.
- Если остаток не равен нулю, то большее число заменяем на меньшее, а меньшее — на остаток.
- Возвращаемся к шагу 1. Процесс продолжается до тех пор, пока на шаге 2 не будет получен остаток, равный нулю. В этот момент последний ненулевой остаток и будет искомым НОД.
Примеры
Найдем НОД(270; 186).
Выполним деление: 270 : 186 = 1 (остаток 84).
Теперь ищем НОД(186; 84).
Выполним деление: 186 : 84 = 2 (остаток 18).
Теперь ищем НОД(84; 18).
Выполним деление: 84 : 18 = 4 (остаток 12).
Теперь ищем НОД(18; 12).
Выполним деление: 18 : 12 = 1 (остаток 6).
Теперь ищем НОД(12; 6).
Выполним деление: 12 : 6 = 2 (остаток 0).
Остаток ноль, значит, НОД(270; 186) = НОД(12; 6) = 6.
Ответ: НОД(270; 186) = 6
Найдем НОД(46; 23).
Выполним деление: 46 : 23 = 2 (остаток 0).
Остаток ноль, значит, НОД(46; 23) = 23.
Ответ: НОД(46; 23) = 23.
Задачи и ответы по теме «Наибольший общий делитель»
Теперь, когда мы разобрали теорию и алгоритмы нахождения наибольшего общего делителя, пришло время применить знания на практике. Решите задачи, чтобы в дальнейшем уверенно работать с НОД.
Ниже под задачами вы найдете подробные решения. Сверьте свои решения, и если найдете ошибку, внимательно разберите ее.
Задача 1
Найдите НОД чисел 36 и 48 методом разложения на простые множители.
Решение и ответ к задаче 1
Разложим на множители:
36 = 22 × 32
48 = 24 × 3
Общие простые множители: 2 и 3.
Выбираем наименьшие степени: 22 и 31.
НОД(36; 48) = 4 × 3 = 12.
Ответ: НОД(36; 48) = 12
Задача 2
Найдите НОД чисел 175 и 140 с помощью алгоритма Евклида.
Решение и ответ к задаче 2
Выполним деление: 175 ÷ 140 = 1 (остаток 35).
Теперь ищем НОД(140; 35).
Выполним деление: 140 ÷ 35 = 4 (остаток 0).
Остаток ноль, значит, НОД(175; 140) = НОД(140; 35) = 35.
Ответ: НОД(175; 140) = 35
Задача 3
Сократите дробь, предварительно найдя НОД числителя и знаменателя: 90/126.
Решение и ответ к задаче 3
Сначала найдем НОД(90; 126). Воспользуемся алгоритмом Евклида.
Выполним деление: 126 : 90 = 1 (остаток 36).
Теперь ищем НОД(90; 36).
Выполним деление: 90 : 36 = 2 (остаток 18).
Теперь ищем НОД(36; 18).
Выполним деление: 36 : 18 = 2 (остаток 0).
Остаток ноль, значит, НОД(90; 126) =18.
Теперь разделим числитель и знаменатель дроби на 18:
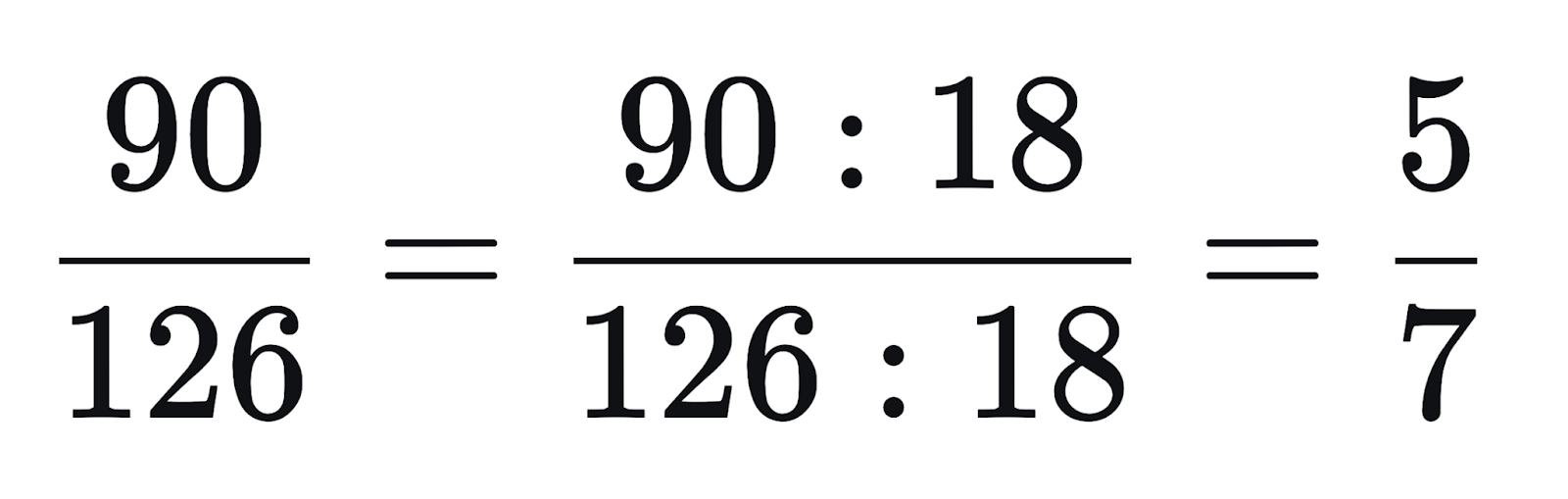
Ответ: 5/7
Задача 4
Какое наибольшее количество одинаковых подарков можно составить из 54 конфет «Ромашка» и 72 конфет «Василек», если все конфеты должны быть использованы?
Решение и ответ к задаче 4
Эта задача сводится к нахождению НОД чисел 54 и 72, так как мы ищем наибольшее число, на которое делятся оба количества конфет.
Найдем НОД(54; 72) с помощью разложения на множители:
54 = 2 × 33
72 = 23 × 32
Общие простые множители: 2 и 3.
Выбираем наименьшие степени: 21 и 32.
НОД(54; 72) = 2 × 9 = 18.
Значит, можно составить 18 одинаковых подарков.
В каждом подарке будет:
Конфет «Ромашка»: 54 : 18 = 3
Конфет «Василек»: 72 : 18 = 4
Ответ: 18 подарков
Популярные вопросы и ответы
Отвечает Анна Жадан, старший преподаватель математики, методист Домашней школы «ИнтернетУрок»:
Чему равен наибольший общий делитель простых чисел?
Простые числа — это натуральные числа, большие 1, которые имеют ровно два различных натуральных делителя: единицу и самого себя.
Наибольшим общим делителем простых чисел может быть только единица.
Наибольшим общим делителем простых чисел может быть только единица.
Почему тему по математике «Наибольший общий делитель» изучают в 5-7 классах?
Тема «Наибольший общий делитель» изучается в 5-7 классах, поскольку именно в этом возрасте ученики начинают в полной мере осваивать важный раздел математики — действия с обыкновенными дробями с разными знаменателями. Для того чтобы выполнить сложение или вычитание обыкновенных дробей, следует привести их к общему знаменателю, для поиска которого и используется алгоритм нахождения НОД. В дальнейшем понятие НОД пригодится для упрощения более сложных, в том числе и буквенных, выражений, ведь алгоритм его нахождения предполагает разложение «больших» чисел и сложных выражений на простые множители. Нахождение НОД — это простая, но важная основа, которая облегчает работу с дробями, подготовит к более сложным темам и развивает системное, логическое мышление.
В каких заданиях ОГЭ и ЕГЭ по математике понадобится умение находить наибольший общий делитель?
Поиск наибольшего общего делителя в ОГЭ и ЕГЭ сводится к заданиям на работу с обыкновенными дробями и дробными выражениями, поскольку он напрямую связан с поиском общего знаменателя. Удобно пользоваться приведением дробей к общему знаменателю для расположения их на координатной прямой — часто встречающееся задание в экзаменах. Кроме того, нахождение НОД пригодится для решения заданий по теории чисел.
