Наименьшее общее кратное (НОК)
Узнаем, что такое наименьшее общее кратное и как его найти. В статье разберем примеры и задачи для закрепления материала
Наименьшее общее кратное используется не только для решения школьных задач, но и в повседневной жизни. Например, учителя используют его при составлении расписаний, программисты создают алгоритмы для поиска НОК и оптимизации вычислений, а инженеры применяют его при синхронизации циклов работы различных механизмов. Давайте узнаем, что представляет собой наименьшее общее кратное чисел и научимся его находить
Что такое наименьшее общее кратное
Наименьшее общее кратное чисел — это наименьшее натуральное число, которое делится на каждое из этих чисел.
Чтобы лучше понять определение, давайте вспомним некоторые термины. Натуральные числа — это числа, которые возникают при счете: 1, 2, 3 и так далее. Кратное число — это натуральное число, которое делится на другое натуральное число без остатка. Например, 27 кратно делится на 3 (27 : 3 = 9).
Следовательно, наименьшее общее кратное двух чисел — это наименьшее число, которое делится без остатка и на первое, и на второе число. Например, для чисел 5 и 9 наименьшим общим кратным будет 45.
Полезная информация о наименьшем общем кратном
| Факт о наименьшем общем кратном | Подробности |
|---|---|
| В школьной программе НОК ищут только для положительных чисел | НОК — это наименьшее натуральное число (1, 2, 3…), а натуральное число не может быть отрицательным (-1, -2, -3…) |
| Если одно из исходных чисел равно нулю, их НОК считается равным нулю | Ноль делится на любое число; «меньше» его могут быть только отрицательные числа |
| НОК можно найти, зная НОД | Перемножьте заданные числа, а затем разделите полученное произведение на их НОД |
| НОК всегда не меньше каждого из чисел, для которых оно находится | НОК делится на любое из исходных чисел без остатка |
Пошаговая инструкция по нахождению НОК
Давайте разберемся на практике, как найти наименьшее общее кратное для двух или нескольких простых чисел. Для примера найдем НОК чисел 84 и 90. Разберем решение по шагам:
Разложите числа на простые множители
Чтобы разложить число на простые множители, начните делить его на простое число 2 и продолжайте, пока это возможно. После этого начинайте деление на следующее простое число (3) и повторяйте деление, пока исходное число не будет разложено полностью.
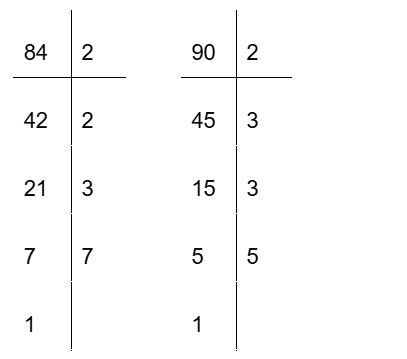
Теперь вы можете выписать разложенные простые множители и возвести в степени те, которые повторяются:
84 = 2² × 3 × 7
90 = 2 × 3² × 5
Выберите максимальные степени простых множителей
Для нахождения НОК вам понадобятся все простые числа в наибольших степенях, которые встречаются в разложениях:
- 2² (так как 84 раскладывается на две двойки, а 90 — на одну, берем наибольшую степень);
- 3² (так как 84 раскладывается на одну тройку, а 90 — на две, снова наибольшую степень);
- 5 (встречается только у 90, берем один раз);
- 7 (встречается только у 84, берем один раз).
Найдите НОК
Чтобы найти наименьшее общее кратное, перемножьте максимальные степени простых множителей:
НОК (84; 90): 2² × 3² × 5 × 7 = 4 × 9 × 5 × 7 = 36 × 35 = 1260
Запишите ответ
Мы получили ответ, который следует записать так:
НОК (84; 90) = 1260
это интересно
Разложение числа на простые множители
Расскажем об умножении простых чисел и разложении числа на простые множители
Подробнее
Примеры нахождения НОК
Чтобы окончательно разобраться в теме, найдем наименьшее общее кратное еще для нескольких чисел.
Найдем НОК для чисел 672 и 945. Начнем с разложения на простые множители:
672 = 2⁵ × 3 × 7
945 = 3³ × 5 × 7
Далее умножим наибольшие степени чисел, которые получились во время разложения:
НОК = 2⁵ × 3³ × 5 × 7 = 32 × 27 × 5 × 7 = 864 × 35 = 30 240
Ответ: НОК (672; 945) = 30 240
Теперь попробуем найти наименьшее общее кратное для трех чисел. Алгоритм решения не меняется — точно так же можно найти НОК для четырех чисел и так далее.
Найдем НОК для чисел 18, 24 и 30. Сначала разложим их на множители:
18 = 2 × 3²
24 = 2³ × 3
30 = 2 × 3 × 5
Потом умножаем наибольшие степени чисел:
НОК = 2³ × 3² × 5 = 8 × 9 × 5 = 360
Мы получили ответ: НОК (18; 24; 30) = 360.
Задачи по теме «Наименьшее общее кратное»
Теперь потренируемся в решении задач.
Задача 1
Найдите наименьшее общее кратное чисел 252 и 378.
Задача 2
Звонок на урок раздается каждые 45 минут, а школьный автобус приезжает на остановку каждые 15 минут. Через сколько минут совпадут звонок и автобус?
Задача 3
Четыре тренера ведут групповые занятия: первый раз в 4 дня, второй — раз в 5 дней, третий — раз в 6 дней, четвертый — раз в 10 дней. Через сколько дней они окажутся в спортзале вчетвером?
Ответы к задачам
Давайте проверим, правильно ли у вас получилось решить задачи.
Задача 1
Чтобы найти НОК 252 и 378, разложим эти числа на простые множители:
252 = 2² × 3² × 7
378 = 2 × 3³ × 7
Далее перемножаем все простые множители в наибольших степенях:
НОК = 2² × 3³ × 7 = 4 × 27 × 7 = 756
Ответ: НОК (252; 378) = 756
Задача 2
Надо найти НОК чисел 45 и 15. Для этого разложим числа на простые множители:
45 = 3² × 5
15 = 3 × 5
Перемножаем простые множители в наибольших степенях:
НОК (45; 15): 3² х 5 = 45
Ответ: НОК (45; 15) = 45
Задача 3
Нужно найти наименьшее общее кратное для чисел 4, 5, 6 и 10. Раскладываем их на простые множители:
4 = 2²
5 = 5
6 = 2 × 3
10 = 2 × 5
Перемножаем максимальные степени чисел:
НОК = 2² × 3 × 5 = 4 × 3 × 5 = 60
Ответ: НОК (4; 5; 6; 10) = 60
Надеемся, теперь у вас не возникнет трудностей во время поиска наименьшего общего кратного чисел.
Популярные вопросы и ответы
Отвечает Евгения Пыжова, преподаватель математики высшей квалификационной категории медико-фармацевтического колледжа города Курска:
Как найти наименьшее общее кратное простых чисел?
Простое число — это число, которое имеет только два делителя: единица и само это число. Например, 11 делится только на 1 и 11. Поэтому, чтобы найти НОК двух простых чисел, нужно найти произведение этих чисел. Например, чтобы найти НОК 5 и 7, нужно их перемножить, и получится 35.
В чем разница между НОД и НОК?
Наименьший общий делитель (НОД) двух чисел — это наибольшее число, на которое делится каждое их этих чисел без остатка. Например, для чисел 12 и 42 наибольшим общим делителем будет 6. Наименьшее общее кратное (НОК) двух чисел — это наименьшее число, которое делится на каждое из этих чисел без остатка. Для чисел 12 и 42 наименьшим общим кратным будет 84.
Почему тему по математике «Наименьшее общее кратное» изучают в 5-7 классах?
Когда начинается изучение дробей и действий между ними, НОК помогает быстро привести дроби к общему знаменателю. Также изучение НОК способствует повышению скорости вычисления и развитию внимания, а это особенно важно при написании проверочных и контрольных работ.
В каких заданиях ОГЭ и ЕГЭ по математике встречается наименьшее общее кратное?
В ОГЭ есть задание №6 «Найдите значение выражения», где нужно выполнить действия (обычно найти произведение суммы или разности смешанных дробей с разными знаменателями и целого числа). В ЕГЭ задание №19, где используется НОК и НОД — текстовые задачи, уравнения, задачи на сократимость дробей, доказательство утверждений.
