Российский математик доказал гипотезу Тота

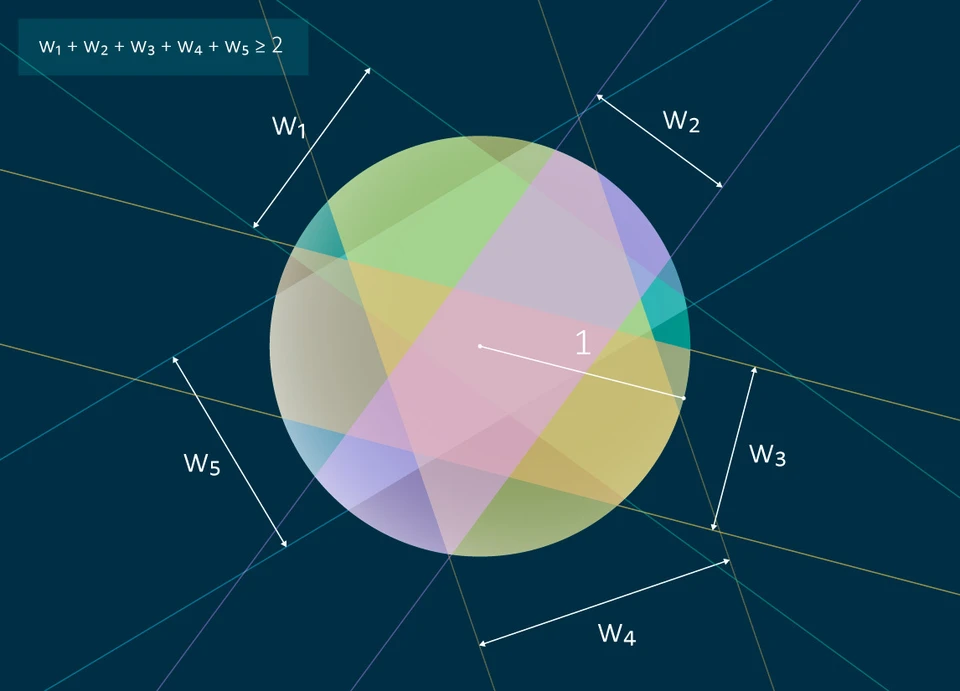
Первая задача на тему гипотезы Тота, решенная еще в прошлом веке - полное покрытие круга полосками так, что их суммарная ширина не меньше 2 (диаметр круга). Каждая из пяти полосок имеет свою ширину и обозначена уникальным цветом.

Ученые Александр Полянский (МФТИ, Россия) и Цзылинь Цзян (Технион, Израиль) доказали гипотезу о покрытии сферы зонами, сформулированную венгерским математиком Ласло Фейешем Тотом еще в 1973 году. Гипотеза изначально была сформулирована так: «Если несколько зон покрывает единичную сферу, то их суммарная ширина по крайней мере π». Новый результат весьма важен для развития дискретной геометрии и дает возможность постановки новых задач в этой области. Соответствующая статья была опубликована в журнале Geometric and Functional Analysis.

Полное покрытие сферы зонами. Каждая из пяти зон имеет свою ширину и обозначена уникальным цветом.

Дискретная геометрия изучает комбинаторные свойства точек, прямых, окружностей, многоугольников и других геометрических объектов. Например, она позволяет ответить на вопросы: какое наибольшее число шаров одинакового размера можно разместить вокруг одного такого же шара. Как наиболее плотно замостить плоскость одинаковыми кругами или пространство одинаковыми шарами. Результаты таких задач сейчас применяются на практике. Например, задача о плотной упаковке позволяет оптимизировать кодирование и исправление ошибок при передаче информации по оптоволокну или радиоканалу.

Желтым цветом на поверхности сферы обозначена одна зона ширины ω.

Гипотеза Ласло Фейеша Тота, тесно связана с другими задачами дискретной геометрии о покрытии какой-либо поверхности полосками. Изначально ставилась задача о покрытии круга полосками, заключенными между параллельными прямыми, более известная как задача о дощечках.

Гипотеза Ласло Фейеш Тота. Покрытие сферы с единичным радиусом зонами одинаковой ширины. Случай минимальной суммарной ширины зон равной π. Каждая зона обозначена уникальным цветом.

Авторы новой работы сосредоточились на «трехмерном», то есть объемном решении варианта гипотезы Тота, в которой рассматривается покрытие сферы особым образом построенными зонами. Каждая из них соответствует определенной трехмерной полоске-«дощечке» - области, заключенной между двумя параллельными плоскостями, расположенными симметрично относительно центра сферы. Математикам было нужно найти минимальную суммарную ширину нескольких таких зон, полностью покрывающих единичную сферу. Ширина исследуемых полосок-«дощечек» в такой задаче равна длине дуги, проходящей через одну дощечку.

Математики решили доказывать гипотезу Тота от противного: в начале предположили что фраза «Если несколько зон покрывает единичную сферу, то их суммарная ширина по крайней мере π» неверна. Тогда сумма ширины зон, полностью покрывающих сферу, должна быть меньше π. Чтобы опровергнуть это утверждение и тем самым доказать теорему им нужно было найти точку, которая лежит на сфере, но не покрыта зонами- «дощечками».

В работе авторы показали, что можно построить такой набор точек в трехмерном пространстве, чтобы по крайней мере одна точка не была покрыта полосками-зонами. Однако все точки, оказывающиеся непокрытыми этими полосками в ходе вычислений оказались за пределами покрываемой сферы. Это противоречит тому, что сумма ширин зон полностью покрывающих сферу меньше π, и доказывает гипотезу Ласло Фейеш Тота для рассмотренного «объемного» случая.